kernel functions

SearchAdvancedHelp

(0.004 seconds)

1—10 of 33 matching pages

1: 10.62 Graphs

§10.62 Graphs

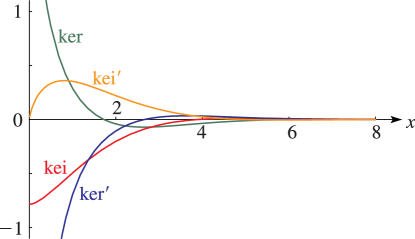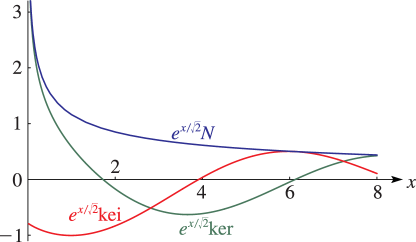►For the modulus functions $M\left(x\right)$ and $N\left(x\right)$ see §10.68(i) with $\nu =0$. … ►

►►

Figure 10.62.2: $\ker x$, $\mathrm{kei}x$, ${\ker }^{\prime }x$, ${\mathrm{kei}}^{\prime }x$, $0\le x\le 8$. Magnify

… ►

►►

Figure 10.62.4: ${\mathrm{e}}^{x/\sqrt{2}}\ker x$, ${\mathrm{e}}^{x/\sqrt{2}}\mathrm{kei}x$, ${\mathrm{e}}^{x/\sqrt{2}}N\left(x\right)$, $0\le x\le 8$. Magnify

2: 10.61 Definitions and Basic Properties

… ►

10.61.2 $${\ker }_{\nu }x+\mathrm{i}{\mathrm{kei}}_{\nu }x={\mathrm{e}}^{-\nu \pi \mathrm{i}/2}{K}_{\nu }\left(x{\mathrm{e}}^{\pi \mathrm{i}/4}\right)=\frac{1}{2}\pi \mathrm{i}{H}_{\nu }^{(1)}\left(x{\mathrm{e}}^{3\pi \mathrm{i}/4}\right)=-\frac{1}{2}\pi \mathrm{i}{\mathrm{e}}^{-\nu \pi \mathrm{i}}{H}_{\nu }^{(2)}\left(x{\mathrm{e}}^{-\pi \mathrm{i}/4}\right).$$

ⓘ

Defines:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function and ${\ker }_{\nu }\left(x\right)$: Kelvin function

Symbols:

$H_{\nu }^{(1)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $H_{\nu }^{(2)}\left(z\right)$: Bessel function of the third kind (or Hankel function), $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $x$: real variable and $\nu$: complex parameter

A&S Ref:

9.9.2

Referenced by:

§10.63(ii), §10.65(ii), §10.67(i), §10.69

Permalink:

http://dlmf.nist.gov/10.61.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.61(i), §10.61 and Ch.10

… ►

10.61.3 $$x^2\frac{d^{2}w}{{dx}^2}+x\frac{dw}{dx}-(\mathrm{i}{x}^2+{\nu }^2)w=0,$$

ⓘ

Symbols:

${\mathrm{bei}}_{\nu }\left(x\right)$: Kelvin function, ${\mathrm{ber}}_{\nu }\left(x\right)$: Kelvin function, ${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\mathrm{i}$: imaginary unit, $x$: real variable and $\nu$: complex parameter

A&S Ref:

9.9.3

Referenced by:

§10.61(ii), §10.68(ii)

Permalink:

http://dlmf.nist.gov/10.61.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.61(ii), §10.61 and Ch.10

►

10.61.4 $$x^4\frac{d^{4}w}{{dx}^4}+2x^3\frac{d^{3}w}{{dx}^3}-(1+2{\nu }^2)\left(x^2\frac{d^{2}w}{{dx}^2}-x\frac{dw}{dx}\right)+({\nu }^4-4{\nu }^2+x^4)w=0,$$ $w={\mathrm{ber}}_{\pm \nu }x,{\mathrm{bei}}_{\pm \nu }x,{\ker }_{\pm \nu }x,{\mathrm{kei}}_{\pm \nu }x$.

ⓘ

Symbols:

${\mathrm{bei}}_{\nu }\left(x\right)$: Kelvin function, ${\mathrm{ber}}_{\nu }\left(x\right)$: Kelvin function, ${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $x$: real variable and $\nu$: complex parameter

A&S Ref:

9.9.4

Referenced by:

§10.61(ii)

Permalink:

http://dlmf.nist.gov/10.61.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.61(ii), §10.61 and Ch.10

… ►

10.61.11 $${\ker }_{\frac{1}{2}}\left(x\sqrt{2}\right)={\mathrm{kei}}_{-\frac{1}{2}}\left(x\sqrt{2}\right)=-2^{-\frac{3}{4}}\sqrt{\frac{\pi }{x}}{\mathrm{e}}^{-x}\sin \left(x-\frac{\pi }{8}\right),$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\sin z$: sine function and $x$: real variable

Referenced by:

§10.61(v)

Permalink:

http://dlmf.nist.gov/10.61.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §10.61(v), §10.61 and Ch.10

►

10.61.12 $${\mathrm{kei}}_{\frac{1}{2}}\left(x\sqrt{2}\right)=-{\ker }_{-\frac{1}{2}}\left(x\sqrt{2}\right)=-2^{-\frac{3}{4}}\sqrt{\frac{\pi }{x}}{\mathrm{e}}^{-x}\cos \left(x-\frac{\pi }{8}\right).$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm and $x$: real variable

Referenced by:

§10.61(v), Ch.10

Permalink:

http://dlmf.nist.gov/10.61.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §10.61(v), §10.61 and Ch.10

3: 10.70 Zeros

§10.70 Zeros

… ►

10.70.1 $$\frac{\mu -1}{16t}+\frac{\mu -1}{32t^2}+\frac{(\mu -1)(5\mu +19)}{1536t^3}+\frac{3{(\mu -1)}^2}{512t^4}+\mathrm{\cdots }.$$

ⓘ

Defines:

$f(t)$: function (locally)

A&S Ref:

9.10.35

Referenced by:

§10.70

Permalink:

http://dlmf.nist.gov/10.70.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.70 and Ch.10

… ►

$$\text{zeros of }{\ker }_{\nu }x\sim \sqrt{2}(t+f(-t)),$$ $t=(m-\frac{1}{2}\nu -\frac{5}{8})\pi$,

… ►In the case $\nu =0$, numerical tabulations (Abramowitz and Stegun (1964, Table 9.12)) indicate that each of (10.70.2) corresponds to the $m$th zero of the function on the left-hand side. …

4: 31.10 Integral Equations and Representations

… ►

Kernel Functions

… ►

31.10.9

ⓘ

Symbols:

: Riemann’s $P$-symbol for solutions of the generalized hypergeometric differential equation, $\cos z$: cosine function, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $\alpha$: real or complex parameter, $\beta$: real or complex parameter, $𝒦(z,t)$: kernel, $\theta$: angle, $\varphi$: angle and $\sigma$: separation constant

Referenced by:

§31.10(i)

Permalink:

http://dlmf.nist.gov/31.10.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §31.10(i), §31.10(i), §31.10 and Ch.31

… ►Fuchs–Frobenius solutions $W_m(z)={\tilde{\kappa }}_m{z}^{-\alpha }H\mathrm{\ell }(1/a,q_m;\alpha ,\alpha -\gamma +1,\alpha -\beta +1,\delta ;1/z)$ are represented in terms of Heun functions $w_m(z)=(0,1){\mathrm{𝐻𝑓}}_m(a,q_m;\alpha ,\beta ,\gamma ,\delta ;z)$ by (31.10.1) with $W(z)=W_m(z)$, $w(z)=w_m(z)$, and with kernel chosen from … ►

Kernel Functions

… ►

31.10.19 $$𝒦(u,v,w)=u^{1-\gamma }{v}^{1-\delta }{w}^{1-ϵ}{𝒞}_{1-\gamma }\left(u\sqrt{{\sigma }_1}\right){𝒞}_{1-\delta }\left(v\sqrt{{\sigma }_2}\right){𝒞}_{1-ϵ}\left(\mathrm{i}w\sqrt{{\sigma }_1+{\sigma }_2}\right),$$

ⓘ

Symbols:

${𝒞}_{\nu }\left(z\right)$: cylinder function, $\mathrm{i}$: imaginary unit, $\gamma$: real or complex parameter, $\delta$: real or complex parameter, $ϵ$: real or complex parameter, $𝒦(z;s,t)$: kernel, $u$ , $v$ , $w$ and ${\sigma }_1$, ${\sigma }_2$: separation constants

Permalink:

http://dlmf.nist.gov/31.10.E19

Encodings:

pMML, png, TeX

See also:

Annotations for §31.10(ii), §31.10(ii), §31.10 and Ch.31

…

5: 10.67 Asymptotic Expansions for Large Argument

… ►

§10.67(i) ${\mathrm{ber}}_{\nu }x,{\mathrm{bei}}_{\nu }x,{\ker }_{\nu }x,{\mathrm{kei}}_{\nu }x$, and Derivatives

… ►

10.67.13 $${\ker }^{2}x+{\mathrm{kei}}^{2}x\sim \frac{\pi }{2x}{\mathrm{e}}^{-x\sqrt{2}}\left(1-\frac{1}{4\sqrt{2}}\frac{1}{x}+\frac{1}{64}\frac{1}{x^2}+\frac{33}{256\sqrt{2}}\frac{1}{x^3}-\frac{1797}{8192}\frac{1}{x^4}+\mathrm{\cdots }\right),$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.31

Permalink:

http://dlmf.nist.gov/10.67.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

►

10.67.14 $$\ker x{\mathrm{kei}}^{\prime }x-{\ker }^{\prime }x\mathrm{kei}x\sim -\frac{\pi }{2x}{\mathrm{e}}^{-x\sqrt{2}}\left(\frac{1}{\sqrt{2}}-\frac{1}{8}\frac{1}{x}+\frac{9}{64\sqrt{2}}\frac{1}{x^2}-\frac{39}{512}\frac{1}{x^3}+\frac{75}{8192\sqrt{2}}\frac{1}{x^4}+\mathrm{\cdots }\right),$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.32

Permalink:

http://dlmf.nist.gov/10.67.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

►

10.67.15 $$\ker x{\ker }^{\prime }x+\mathrm{kei}x{\mathrm{kei}}^{\prime }x\sim -\frac{\pi }{2x}{\mathrm{e}}^{-x\sqrt{2}}\left(\frac{1}{\sqrt{2}}+\frac{3}{8}\frac{1}{x}-\frac{15}{64\sqrt{2}}\frac{1}{x^2}+\frac{45}{512}\frac{1}{x^3}+\frac{315}{8192\sqrt{2}}\frac{1}{x^4}+\mathrm{\cdots }\right),$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.33

Permalink:

http://dlmf.nist.gov/10.67.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

►

10.67.16 $${\left({\ker }^{\prime }x\right)}^2+{\left({\mathrm{kei}}^{\prime }x\right)}^2\sim \frac{\pi }{2x}{\mathrm{e}}^{-x\sqrt{2}}\left(1+\frac{3}{4\sqrt{2}}\frac{1}{x}+\frac{9}{64}\frac{1}{x^2}-\frac{75}{256\sqrt{2}}\frac{1}{x^3}+\frac{2475}{8192}\frac{1}{x^4}+\mathrm{\cdots }\right).$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

A&S Ref:

9.10.34

Permalink:

http://dlmf.nist.gov/10.67.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §10.67(ii), §10.67 and Ch.10

6: 10.63 Recurrence Relations and Derivatives

… ►

§10.63(i) ${\mathrm{ber}}_{\nu }x$, ${\mathrm{bei}}_{\nu }x$, ${\ker }_{\nu }x$, ${\mathrm{kei}}_{\nu }x$

… ►

$\sqrt{2}{\mathrm{kei}}^{\prime }x=-{\ker }_{1}x+{\mathrm{kei}}_{1}x.$

…

7: 10.69 Uniform Asymptotic Expansions for Large Order

… ►

10.69.3 $${\ker }_{\nu }\left(\nu x\right)+\mathrm{i}{\mathrm{kei}}_{\nu }\left(\nu x\right)\sim {\mathrm{e}}^{-\nu \xi }{\left(\frac{\pi }{2\nu \xi }\right)}^{1/2}{\left(\frac{x{\mathrm{e}}^{3\pi \mathrm{i}/4}}{1+\xi }\right)}^{-\nu }\sum _{k=0}^{\mathrm{\infty }}{(-1)}^k\frac{U_k({\xi }^{-1})}{{\nu }^k},$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $k$: nonnegative integer, $x$: real variable, $\nu$: complex parameter, $U_k(p)$: polynomial coefficient and $\xi$

A&S Ref:

9.10.38

Permalink:

http://dlmf.nist.gov/10.69.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.69 and Ch.10

… ►

10.69.5 $${\ker }_{\nu }^{\prime }\left(\nu x\right)+\mathrm{i}{\mathrm{kei}}_{\nu }^{\prime }\left(\nu x\right)\sim -\frac{{\mathrm{e}}^{-\nu \xi }}{x}{\left(\frac{\pi \xi }{2\nu }\right)}^{1/2}{\left(\frac{x{\mathrm{e}}^{3\pi \mathrm{i}/4}}{1+\xi }\right)}^{-\nu }\sum _{k=0}^{\mathrm{\infty }}{(-1)}^k\frac{V_k({\xi }^{-1})}{{\nu }^k},$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\sim$: Poincaré asymptotic expansion, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $k$: nonnegative integer, $x$: real variable, $\nu$: complex parameter, $V_k(p)$: polynomial coefficient and $\xi$

A&S Ref:

9.10.40

Permalink:

http://dlmf.nist.gov/10.69.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.69 and Ch.10

…

8: 28.10 Integral Equations

… ►

§28.10(i) Equations with Elementary Kernels

… ►

§28.10(ii) Equations with Bessel-Function Kernels

…

9: 10.68 Modulus and Phase Functions

… ►

10.68.2 $$N_{\nu }\left(x\right){\mathrm{e}}^{\mathrm{i}{\varphi }_{\nu }\left(x\right)}={\ker }_{\nu }x+\mathrm{i}{\mathrm{kei}}_{\nu }x,$$

ⓘ

Symbols:

${\mathrm{kei}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $N_{\nu }\left(x\right)$: modulus of derivatives of Bessel functions, ${\varphi }_{\nu }\left(x\right)$: phase of derivatives of Bessel functions, $x$: real variable and $\nu$: complex parameter

Permalink:

http://dlmf.nist.gov/10.68.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.68(i), §10.68 and Ch.10

…

10: 10.65 Power Series

… ►

10.65.3 $${\ker }_{n}x=\frac{1}{2}{(\frac{1}{2}x)}^{-n}\sum _{k=0}^{n-1}\frac{(n-k-1)!}{k!}\cos \left(\frac{3}{4}n\pi +\frac{1}{2}k\pi \right){(\frac{1}{4}{x}^2)}^k-\ln \left(\frac{1}{2}x\right){\mathrm{ber}}_{n}x+\frac{1}{4}\pi {\mathrm{bei}}_{n}x+\frac{1}{2}{(\frac{1}{2}x)}^n\sum _{k=0}^{\mathrm{\infty }}\frac{\psi \left(k+1\right)+\psi \left(n+k+1\right)}{k!(n+k)!}\cos \left(\frac{3}{4}n\pi +\frac{1}{2}k\pi \right){(\frac{1}{4}{x}^2)}^k,$$

ⓘ

Symbols:

${\mathrm{bei}}_{\nu }\left(x\right)$: Kelvin function, ${\mathrm{ber}}_{\nu }\left(x\right)$: Kelvin function, ${\ker }_{\nu }\left(x\right)$: Kelvin function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\psi \left(z\right)$: psi (or digamma) function, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $n$: integer, $k$: nonnegative integer and $x$: real variable

A&S Ref:

9.9.11

Permalink:

http://dlmf.nist.gov/10.65.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.65(ii), §10.65 and Ch.10

…