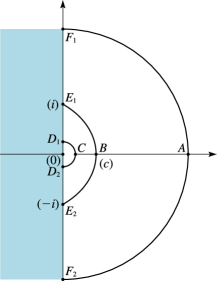10 Bessel Functions Modified Bessel Functions 10.40 Asymptotic Expansions for Large Argument 10.42 Zeros

§10.41 Asymptotic Expansions for Large Order

Keywords:: modified Bessel functions
Referenced by:: §10.57
Permalink:: http://dlmf.nist.gov/10.41

§10.41(i) Asymptotic Forms
§10.41(ii) Uniform Expansions for Real Variable
§10.41(iii) Uniform Expansions for Complex Variable
§10.41(iv) Double Asymptotic Properties
§10.41(v) Double Asymptotic Properties (Continued)

§10.41(i) Asymptotic Forms

Notes:: Combine (10.19.1), (10.19.2) with (10.27.6), (10.27.8).
Keywords:: modified Bessel functions
Permalink:: http://dlmf.nist.gov/10.41.i

If $\nu\to\infty$ through positive real values with $z(\neq 0)$ fixed, then

10.41.1 $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)\sim\frac{1}{\sqrt{2\pi\nu}}\left% (\frac{ez}{2\nu}\right)^{\nu},$

Symbols:: : base of exponential function, $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\sim$ : asymptotic equality, : complex variable and $\nu$ : complex parameter
Permalink:: http://dlmf.nist.gov/10.41.E1
Encodings:: TeX, pMML, png

10.41.2 $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)\sim\sqrt{\frac{\pi}{2\nu}}\left(% \frac{ez}{2\nu}\right)^{{-\nu}}.$

Symbols:: : base of exponential function, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\sim$ : asymptotic equality, : complex variable and $\nu$ : complex parameter
Permalink:: http://dlmf.nist.gov/10.41.E2
Encodings:: TeX, pMML, png

§10.41(ii) Uniform Expansions for Real Variable

Notes:: See Olver (1997b, pp. 374–378).
Keywords:: derivatives, modified Bessel functions
Referenced by:: §10.19(ii), §10.20(i), §10.41(v), §10.69, §10.69, §10.75(v)
Permalink:: http://dlmf.nist.gov/10.41.ii

As $\nu\to\infty$ through positive real values,

10.41.3 $\mathop{I_{{\nu}}\/}\nolimits\!\left(\nu z\right)\sim\frac{e^{{\nu\eta}}}{(2% \pi\nu)^{{\frac{1}{2}}}(1+z^{2})^{{\frac{1}{4}}}}\sum_{{k=0}}^{\infty}\frac{U_% {k}(p)}{\nu^{k}},$

Symbols:: : base of exponential function, $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\eta$ and $U_{k}(p)$ : polynomials
A&S Ref:: 9.7.7
Referenced by:: §10.41(iii), §10.41(iv)
Permalink:: http://dlmf.nist.gov/10.41.E3
Encodings:: TeX, pMML, png

10.41.4 $\mathop{K_{{\nu}}\/}\nolimits\!\left(\nu z\right)\sim\left(\frac{\pi}{2\nu}% \right)^{{\frac{1}{2}}}\frac{e^{{-\nu\eta}}}{(1+z^{2})^{{\frac{1}{4}}}}\sum_{{% k=0}}^{\infty}(-1)^{k}\frac{U_{k}(p)}{\nu^{k}},$

Symbols:: : base of exponential function, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\eta$ and $U_{k}(p)$ : polynomials
A&S Ref:: 9.7.8
Permalink:: http://dlmf.nist.gov/10.41.E4
Encodings:: TeX, pMML, png

10.41.5 ${\mathop{I_{{\nu}}\/}\nolimits^{{\prime}}}\!\left(\nu z\right)\sim\frac{(1+z^{% 2})^{{\frac{1}{4}}}e^{{\nu\eta}}}{(2\pi\nu)^{{\frac{1}{2}}}z}\sum_{{k=0}}^{% \infty}\frac{V_{k}(p)}{\nu^{k}},$

Symbols:: : base of exponential function, $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\eta$ and $V_{k}(p)$ : polynomials
A&S Ref:: 9.7.9
Referenced by:: §10.41(iv)
Permalink:: http://dlmf.nist.gov/10.41.E5
Encodings:: TeX, pMML, png

10.41.6 ${\mathop{K_{{\nu}}\/}\nolimits^{{\prime}}}\!\left(\nu z\right)\sim-\left(\frac% {\pi}{2\nu}\right)^{{\frac{1}{2}}}\frac{(1+z^{2})^{{\frac{1}{4}}}e^{{-\nu\eta}% }}{z}\sum_{{k=0}}^{\infty}(-1)^{k}\frac{V_{k}(p)}{\nu^{k}},$

Symbols:: : base of exponential function, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\sim$ : asymptotic equality, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\eta$ and $V_{k}(p)$ : polynomials
A&S Ref:: 9.7.10
Referenced by:: §10.41(iii), §10.41(iv)
Permalink:: http://dlmf.nist.gov/10.41.E6
Encodings:: TeX, pMML, png

uniformly for $0<z<\infty$ . Here

10.41.7 $\eta=(1+z^{2})^{{\frac{1}{2}}}+\mathop{\ln\/}\nolimits\frac{z}{1+(1+z^{2})^{{% \frac{1}{2}}}},$

Symbols:: $\mathop{\ln\/}\nolimits z$ : principal branch of logarithm function, : complex variable and $\eta$
A&S Ref:: 9.7.11
Permalink:: http://dlmf.nist.gov/10.41.E7
Encodings:: TeX, pMML, png

10.41.8 $p=(1+z^{2})^{{-\frac{1}{2}}},$

Symbols:: : complex variable
A&S Ref:: 9.7.11
Referenced by:: §10.41(iii)
Permalink:: http://dlmf.nist.gov/10.41.E8
Encodings:: TeX, pMML, png

where the branches assume their principal values. Also, $U_{k}(p)$ and $V_{k}(p)$ are polynomials in of degree , given by $U_{0}(p)=V_{0}(p)=1$ , and

10.41.9

$U_{{k+1}}(p)=\tfrac{1}{2}p^{2}(1-p^{2})U_{k}^{{\prime}}(p)+\frac{1}{8}\int_{0}% ^{p}(1-5t^{2})U_{k}(t)dt,$

$V_{{k+1}}(p)=U_{{k+1}}(p)-\tfrac{1}{2}p(1-p^{2})U_{k}(p)-p^{2}(1-p^{2})U_{k}^{% {\prime}}(p),$ $k=0,1,2,\ldots$ .

Symbols:: : differential of , $\int$ : integral, : nonnegative integer, $U_{k}(p)$ : polynomials and $V_{k}(p)$ : polynomials
A&S Ref:: 9.3.10, 9.3.14
Permalink:: http://dlmf.nist.gov/10.41.E9
Encodings:: TeX, TeX, pMML, pMML, png, png

For ,

10.41.10

$U_{1}(p)=\tfrac{1}{24}(3p-5p^{3}),$

$U_{2}(p)=\tfrac{1}{1152}(81p^{2}-462p^{4}+385p^{6}),$

$U_{3}(p)=\tfrac{1}{4\;14720}\*(30375p^{3}-3\;69603p^{5}+7\;65765p^{7}-4\;25425% p^{9}),$

Symbols:: $U_{k}(p)$ : polynomials
A&S Ref:: 9.3.9
Permalink:: http://dlmf.nist.gov/10.41.E10
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

10.41.11

$V_{1}(p)=\tfrac{1}{24}(-9p+7p^{3}),$

$V_{2}(p)=\tfrac{1}{1152}(-135p^{2}+594p^{4}-455p^{6}),$

$V_{3}(p)=\tfrac{1}{4\;14720}\*(-42525p^{3}+4\;51737p^{5}-8\;83575p^{7}+4\;7547% 5p^{9}).$

Symbols:: $V_{k}(p)$ : polynomials
A&S Ref:: 9.3.13
Permalink:: http://dlmf.nist.gov/10.41.E11
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

For $U_{4}(p)$ , $U_{5}(p)$ , $U_{6}(p)$ , see Bickley et al. (1952, p. xxxv).

For numerical tables of $\eta=\eta(z)$ and the coefficients $U_{k}(p)$ , $V_{k}(p)$ , see Olver (1962, pp. 43–51).

§10.41(iii) Uniform Expansions for Complex Variable

Keywords:: derivatives, modified Bessel functions
Referenced by:: §10.69
Permalink:: http://dlmf.nist.gov/10.41.iii

The expansions (10.41.3)–(10.41.6) also hold uniformly in the sector $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{1}{2}\pi-\delta$ $(<\tfrac{1}{2}\pi)$ , with the branches of the fractional powers in (10.41.3)–(10.41.8) extended by continuity from the positive real -axis.

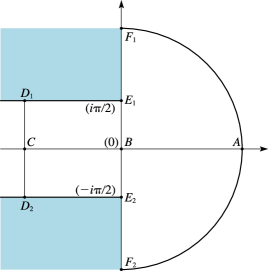
Figures 10.41.1 and 10.41.2 show corresponding points of the mapping of the -plane and the $\eta$ -plane. The curve $E_{1}BE_{2}$ in the -plane is the upper boundary of the domain $\mathbf{K}$ depicted in Figure 10.20.3 and rotated through an angle $-\tfrac{1}{2}\pi$ . Thus is the point , where is given by (10.20.18).

For derivations of the results in this subsection, and also error bounds, see Olver (1997b, pp. 374–378). For extensions of the regions of validity in the -plane and extensions to complex values of $\nu$ see Olver (1997b, pp. 378–382).

Figure 10.41.1:

-plane.

Symbols:: : nonnegative integer, : complex variable, $F_{k}$ : points, : point, : point, : point, $D_{k}$ : points and $E_{k}$ : points
Referenced by:: §10.41(iii)
Permalink:: http://dlmf.nist.gov/10.41.F1
Encodings:: pdf, png

Figure 10.41.2: $\eta$ -plane.

Symbols:: $\eta$
Referenced by:: §10.41(iii)
Permalink:: http://dlmf.nist.gov/10.41.F2
Encodings:: pdf, png

For expansions in inverse factorial series see Dunster et al. (1993).

§10.41(iv) Double Asymptotic Properties

Keywords:: asymptotic approximations and expansions, modified Bessel functions
Referenced by:: §10.69, §12.10(vi), Methodology
Permalink:: http://dlmf.nist.gov/10.41.iv

The series (10.41.3)–(10.41.6) can also be regarded as generalized asymptotic expansions for large . Thus as $z\to\infty$ with $\ell$ $(\geq 1)$ and $\nu$ both fixed,

10.41.12 $\mathop{I_{{\nu}}\/}\nolimits\!\left(\nu z\right)=\frac{e^{{\nu\eta}}}{(2\pi% \nu)^{{\frac{1}{2}}}(1+z^{2})^{{\frac{1}{4}}}}\left(\sum_{{k=0}}^{{\ell-1}}% \frac{U_{k}(p)}{\nu^{k}}+\mathop{O\/}\nolimits\left(\frac{1}{z^{\ell}}\right)% \right),$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{1}{2}\pi-\delta$ ,

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : base of exponential function, $\mathop{I_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\delta$ : small positive constant, $\eta$ , and $U_{k}(p)$ : polynomials
Referenced by:: §10.41(iv)
Permalink:: http://dlmf.nist.gov/10.41.E12
Encodings:: TeX, pMML, png

10.41.13 $\mathop{K_{{\nu}}\/}\nolimits\!\left(\nu z\right)=\left(\frac{\pi}{2\nu}\right% )^{{\frac{1}{2}}}\frac{e^{{-\nu\eta}}}{(1+z^{2})^{{\frac{1}{4}}}}\*\left(\sum_% {{k=0}}^{{\ell-1}}(-1)^{k}\frac{U_{k}(p)}{\nu^{k}}+\mathop{O\/}\nolimits\left(% \frac{1}{z^{\ell}}\right)\right),$ $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\tfrac{3}{2}\pi-\delta$ .

Symbols:: $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : base of exponential function, $\mathop{K_{{\nu}}\/}\nolimits\!\left(z\right)$ : modified Bessel function, $\mathop{\mathrm{ph}\/}\nolimits$ : phase, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $\delta$ : small positive constant, $\eta$ , and $U_{k}(p)$ : polynomials
Referenced by:: §10.41(iv), §10.41(iv)
Permalink:: http://dlmf.nist.gov/10.41.E13
Encodings:: TeX, pMML, png

Similarly for (10.41.5) and (10.41.6).

In the case of (10.41.13) with positive real values of the result is a consequence of the error bounds given in Olver (1997b, pp. 377–378). Then by expanding the quantities $\eta$ , $(1+z^{2})^{{-\frac{1}{4}}}$ , and $U_{k}(p)$ , $k=0,1,\ldots,\ell-1$ , and rearranging, we arrive at an expansion of the right-hand side of (10.41.13) in powers of $z^{{-1}}$ . Moreover, because of the uniqueness property of asymptotic expansions (§2.1(iii)) this expansion must agree with (10.40.2), with replaced by $\nu z$ , up to and including the term in $z^{{-(\ell-1)}}$ . It also enjoys the same sector of validity.

To establish (10.41.12) we substitute into (10.34.3), with and replaced by $\nu z$ , by means of (10.41.13) observing that when is large the effect of replacing by $ze^{{\pm\pi i}}$ is to replace $\eta$ , $(1+z^{2})^{{\frac{1}{4}}}$ , and by $-\eta$ , $\pm i(1+z^{2})^{{\frac{1}{4}}}$ , and , respectively.

§10.41(v) Double Asymptotic Properties (Continued)

Keywords:: Bessel functions, Hankel functions, asymptotic approximations and expansions, modified Bessel functions
Referenced by:: §10.20(iii), §10.74(i), ¶ ‣ §12.10(vii), Methodology
Permalink:: http://dlmf.nist.gov/10.41.v

Similar analysis can be developed for the uniform asymptotic expansions in terms of Airy functions given in §10.20. We first prove that for the expansions (10.20.6) for the Hankel functions $\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(\nu z\right)$ and $\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits\!\left(\nu z\right)$ the -asymptotic property applies when $z\to\pm i\infty$ , respectively. This is a consequence of the error bounds associated with these expansions. We then extend the validity of this property from $z\to\pm i\infty$ to $z\to\infty$ in the sector $-\pi+\delta\leq\mathop{\mathrm{ph}\/}\nolimits z\leq 2\pi-\delta$ in the case of $\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(\nu z\right)$ , and to $z\to\infty$ in the sector $-2\pi+\delta\leq\mathop{\mathrm{ph}\/}\nolimits z\leq\pi-\delta$ in the case of $\mathop{{H^{{(2)}}_{{\nu}}}\/}\nolimits\!\left(\nu z\right)$ . This is done by re-expansion with the aid of (10.20.10), (10.20.11), and §10.41(ii), followed by comparison with (10.17.5) and (10.17.6), with replaced by $\nu z$ . Lastly, we substitute into (10.4.4), again with replaced by $\nu z$ . The final results are:

10.41.14 $\mathop{J_{{\nu}}\/}\nolimits\!\left(\nu z\right)=\left(\frac{4\zeta}{1-z^{2}}% \right)^{{\frac{1}{4}}}\left(\frac{\mathop{\mathrm{Ai}\/}\nolimits\!\left(\nu^% {{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{1}{3}}}}\left(\sum_{{k=0}}^{\ell}% \frac{A_{k}(\zeta)}{\nu^{{2k}}}+\mathop{O\/}\nolimits\left(\frac{1}{\zeta^{{3% \ell+3}}}\right)\right)+\frac{{\mathop{\mathrm{Ai}\/}\nolimits^{{\prime}}}\!% \left(\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{5}{3}}}}\left(\sum_{{k=0}}^% {{\ell-1}}\frac{B_{k}(\zeta)}{\nu^{{2k}}}+\mathop{O\/}\nolimits\left(\frac{1}{% \zeta^{{3\ell+1}}}\right)\right)\right),$

Symbols:: $\mathop{\mathrm{Ai}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{J_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the first kind, $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $A_{k}(\zeta)$ : coefficients and $B_{k}(\zeta)$ : coefficients
Referenced by:: §10.41(v)
Permalink:: http://dlmf.nist.gov/10.41.E14
Encodings:: TeX, pMML, png

10.41.15 $\mathop{Y_{{\nu}}\/}\nolimits\!\left(\nu z\right)=-\left(\frac{4\zeta}{1-z^{2}% }\right)^{{\frac{1}{4}}}\left(\frac{\mathop{\mathrm{Bi}\/}\nolimits\!\left(\nu% ^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{1}{3}}}}\left(\sum_{{k=0}}^{\ell}% \frac{A_{k}(\zeta)}{\nu^{{2k}}}+\mathop{O\/}\nolimits\left(\frac{1}{\zeta^{{3% \ell+3}}}\right)\right)+\frac{{\mathop{\mathrm{Bi}\/}\nolimits^{{\prime}}}\!% \left(\nu^{{\frac{2}{3}}}\zeta\right)}{\nu^{{\frac{5}{3}}}}\left(\sum_{{k=0}}^% {{\ell-1}}\frac{B_{k}(\zeta)}{\nu^{{2k}}}+\mathop{O\/}\nolimits\left(\frac{1}{% \zeta^{{3\ell+1}}}\right)\right)\right),$

Symbols:: $\mathop{\mathrm{Bi}\/}\nolimits\!\left(z\right)$ : Airy function, $\mathop{Y_{{\nu}}\/}\nolimits\!\left(z\right)$ : Bessel function of the second kind, $\mathop{O\/}\nolimits\!\left(x\right)$ : order not exceeding, : nonnegative integer, : complex variable, $\nu$ : complex parameter, $A_{k}(\zeta)$ : coefficients and $B_{k}(\zeta)$ : coefficients
Referenced by:: §10.41(v)
Permalink:: http://dlmf.nist.gov/10.41.E15
Encodings:: TeX, pMML, png

as $z\to\infty$ in $|\mathop{\mathrm{ph}\/}\nolimits z|\leq\pi-\delta$ , or equivalently as $\zeta\to\infty$ in $|\mathop{\mathrm{ph}\/}\nolimits(-\zeta)|\leq\tfrac{2}{3}\pi-\delta$ , for fixed $\ell$ $(\geq 0)$ and fixed $\nu$ .

It needs to be noted that the results (10.41.14) and (10.41.15) do not apply when $z\to 0+$ or equivalently $\zeta\to+\infty$ . This is because $A_{k}(\zeta)$ and $\zeta^{{-\frac{1}{2}}}B_{k}(\zeta),k=0,1,\ldots$ , do not form an asymptotic scale (§2.1(v)) as $\zeta\to+\infty$ ; see Olver (1997b, pp. 422–425).

© 2010–2013 NIST / Privacy Policy / Disclaimer / Feedback; Version 1.0.6; Release date 2013-05-06 Math-Image version (See MathML) . A Printed Companionis available. 10.40 Asymptotic Expansions for Large Argument 10.42 Zeros