exponential function

SearchAdvancedHelp

(0.017 seconds)

21—30 of 414 matching pages

21: 8.24 Physical Applications

§8.24 Physical Applications

… ►The function $\gamma (a,x)$ appears in: discussions of power-law relaxation times in complex physical systems (Sornette (1998)); logarithmic oscillations in relaxation times for proteins (Metzler et al. (1999)); Gaussian orbitals and exponential (Slater) orbitals in quantum chemistry (Shavitt (1963), Shavitt and Karplus (1965)); population biology and ecological systems (Camacho et al. (2002)). … ►The function $E_p\left(x\right)$, with $p>0$, appears in theories of transport and radiative equilibrium (Hopf (1934), Kourganoff (1952), Altaç (1996)). ►With more general values of $p$, $E_p\left(x\right)$ supplies fundamental auxiliary functions that are used in the computation of molecular electronic integrals in quantum chemistry (Harris (2002), Shavitt (1963)), and also wave acoustics of overlapping sound beams (Ding (2000)).

22: 13.18 Relations to Other Functions

… ►

13.18.3 $$M_{\kappa ,-\kappa -\frac{1}{2}}\left(z\right)={\mathrm{e}}^{\frac{1}{2}z}{z}^{-\kappa }.$$

ⓘ

Symbols:

$M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.18.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(i), §13.18 and Ch.13

… ►When $\frac{1}{2}-\kappa \pm \mu$ is an integer the Whittaker functions can be expressed as incomplete gamma functions (or generalized exponential integrals). … ►

13.18.4 $$M_{\mu -\frac{1}{2},\mu }\left(z\right)=2\mu {\mathrm{e}}^{\frac{1}{2}z}{z}^{\frac{1}{2}-\mu }\gamma (2\mu ,z),$$

ⓘ

Symbols:

$M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $\gamma (a,z)$: incomplete gamma function and $z$: complex variable

Referenced by:

§8.5

Permalink:

http://dlmf.nist.gov/13.18.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(ii), §13.18 and Ch.13

►

13.18.5 $$W_{\mu -\frac{1}{2},\mu }\left(z\right)={\mathrm{e}}^{\frac{1}{2}z}{z}^{\frac{1}{2}-\mu }\mathrm{\Gamma }(2\mu ,z).$$

ⓘ

Symbols:

$W_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $\mathrm{\Gamma }(a,z)$: incomplete gamma function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.18.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(ii), §13.18 and Ch.13

… ►

13.18.6 $$M_{-\frac{1}{4},\frac{1}{4}}\left(z^2\right)=\frac{1}{2}{\mathrm{e}}^{\frac{1}{2}{z}^2}\sqrt{\pi z}\mathrm{erf}\left(z\right),$$

ⓘ

Symbols:

$M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{erf}z$: error function, $\mathrm{e}$: base of natural logarithm and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.18.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(ii), §13.18 and Ch.13

…

23: 5.6 Inequalities

… ►

5.6.1

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $x$: real variable

Referenced by:

§5.6(i)

Permalink:

http://dlmf.nist.gov/5.6.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §5.6(i), §5.6 and Ch.5

… ►

5.6.5 $$\exp \left((1-s)\psi \left(x+s^{1/2}\right)\right)\le \frac{\mathrm{\Gamma }\left(x+1\right)}{\mathrm{\Gamma }\left(x+s\right)}\le \exp \left((1-s)\psi \left(x+\frac{1}{2}(s+1)\right)\right),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\psi \left(z\right)$: psi (or digamma) function, $\exp z$: exponential function, $s$: real or complex variable and $x$: real variable

Referenced by:

§5.6(i)

Permalink:

http://dlmf.nist.gov/5.6.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §5.6(i), §5.6(i), §5.6 and Ch.5

… ►

5.6.9 $$|\mathrm{\Gamma }\left(z\right)|\le {(2\pi )}^{1/2}{|z|}^{x-(1/2)}{\mathrm{e}}^{-\pi |y|/2}\exp \left(\frac{1}{6}{|z|}^{-1}\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function, $\mathrm{e}$: base of natural logarithm, $x$: real variable, $y$: real variable and $z$: complex variable

Referenced by:

§5.6(ii)

Permalink:

http://dlmf.nist.gov/5.6.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §5.6(ii), §5.6 and Ch.5

24: 4.9 Continued Fractions

… ►

§4.9(ii) Exponentials

… ►For other continued fractions involving the exponential function see Lorentzen and Waadeland (1992, pp. 563–564). …

25: 18.32 OP’s with Respect to Freud Weights

… ►

18.32.1 $$w(x)=\exp \left(-Q(x)\right),$$ ,

ⓘ

Symbols:

$\exp z$: exponential function, $w(x)$: weight function and $x$: real variable

Referenced by:

§18.32

Permalink:

http://dlmf.nist.gov/18.32.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §18.32 and Ch.18

… ►

18.32.2 $$w(x)={\left|x\right|}^{\alpha }\exp \left(-Q(x)\right),$$ $x\in ℝ$, $\alpha >-1$,

ⓘ

Symbols:

$\in$: element of, $\exp z$: exponential function, $ℝ$: real line, $w(x)$: weight function and $x$: real variable

Referenced by:

§18.32, Erratum (V1.2.0) Section 18.32

Permalink:

http://dlmf.nist.gov/18.32.E2

Encodings:

pMML, png, TeX

Addition (effective with 1.2.0):

This equation was added.

See also:

Annotations for §18.32 and Ch.18

…

26: 36.2 Catastrophes and Canonical Integrals

… ►

36.2.6 $${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)=2\sqrt{\pi /3}\exp \left(\mathrm{i}\left(\frac{4}{27}{z}^3+\frac{1}{3}xz-\frac{1}{4}\pi \right)\right){\int }_{\mathrm{\infty }\exp \left(-7\pi \mathrm{i}/12\right)}^{\mathrm{\infty }\exp \left(\pi \mathrm{i}/12\right)}\exp \left(\mathrm{i}\left(u^6+2z{u}^4+(z^2+x)u^2+\frac{y^2}{12u^2}\right)\right)du,$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, $\exp z$: exponential function, $\mathrm{i}$: imaginary unit, $\int$: integral, $y$: real parameter, $z$: real parameter and $x$: real parameter

Referenced by:

§36.2(i), §36.2(ii), §36.5(iii)

Permalink:

http://dlmf.nist.gov/36.2.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §36.2(i), §36.2(i), §36.2 and Ch.36

… ►

36.2.12 $${\mathrm{\Psi }}_0=\sqrt{\pi }\exp \left(\mathrm{i}\frac{\pi }{4}\right).$$

ⓘ

Symbols:

${\mathrm{\Psi }}_K\left(𝐱\right)$: canonical integral function, $\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function and $\mathrm{i}$: imaginary unit

Referenced by:

§36.2(ii)

Permalink:

http://dlmf.nist.gov/36.2.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §36.2(ii), §36.2 and Ch.36

… ►

36.2.15

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\mathrm{\Psi }}_K\left(𝐱\right)$: canonical integral function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\exp z$: exponential function, $\mathrm{i}$: imaginary unit and $K$: codimension

Referenced by:

§36.2(ii)

Permalink:

http://dlmf.nist.gov/36.2.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §36.2(ii), §36.2 and Ch.36

… ►

36.2.28 $${\mathrm{\Psi }}^{(\mathrm{E})}\left(0,0,z\right)=\overline{{\mathrm{\Psi }}^{(\mathrm{E})}\left(0,0,-z\right)}=2\pi \sqrt{\frac{\pi z}{27}}\exp \left(\frac{2}{27}\mathrm{i}{z}^3\right)\left(J_{-1/6}\left(\frac{2}{27}{z}^3\right)+\mathrm{i}{J}_{1/6}\left(\frac{2}{27}{z}^3\right)\right),$$ $z\ge 0$,

ⓘ

Symbols:

$J_{\nu }\left(z\right)$: Bessel function of the first kind, $\pi$: the ratio of the circumference of a circle to its diameter, $\overline{z}$: complex conjugate, ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, $\exp z$: exponential function, $\mathrm{i}$: imaginary unit and $z$: real parameter

Referenced by:

Erratum (V1.0.5) for Chapters 8, 20, 36

Permalink:

http://dlmf.nist.gov/36.2.E28

Encodings:

pMML, png, TeX

Addition (effective with 1.0.5):

This equation has been added. For the proof see Berry and Howls (2010).

See also:

Annotations for §36.2(iv), §36.2 and Ch.36

►

36.2.29 $${\mathrm{\Psi }}^{(\mathrm{H})}\left(0,0,z\right)=\overline{{\mathrm{\Psi }}^{(\mathrm{H})}\left(0,0,-z\right)}=\frac{2^{1/3}}{\sqrt{3}}\exp \left(\frac{1}{27}\mathrm{i}{z}^3\right){\mathrm{\Psi }}^{(\mathrm{E})}\left(0,0,-\frac{z}{2^{2/3}}\right),$$ .

ⓘ

Symbols:

$\overline{z}$: complex conjugate, ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, $\exp z$: exponential function, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit and $z$: real parameter

Referenced by:

Erratum (V1.0.5) for Chapters 8, 20, 36

Permalink:

http://dlmf.nist.gov/36.2.E29

Encodings:

pMML, png, TeX

Addition (effective with 1.0.5):

This equation has been added. For the proof see Berry and Howls (2010).

See also:

Annotations for §36.2(iv), §36.2 and Ch.36

27: 10.56 Generating Functions

… ►

10.56.5 $$\frac{\exp \left(-\sqrt{z^2+2\mathrm{i}zt}\right)}{z}=\frac{{\mathrm{e}}^{-z}}{z}+\frac{2}{\pi }\sum _{n=1}^{\mathrm{\infty }}\frac{{(-\mathrm{i}t)}^n}{n!}{𝗄}_{n-1}\left(z\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.56, Ch.10

Permalink:

http://dlmf.nist.gov/10.56.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

28: 4.8 Identities

… ►

4.8.8 $$\mathrm{Ln}\left(\exp z\right)=z+2k\pi \mathrm{i},$$ $k\in \mathbb{Z}$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\in$: element of, $\exp z$: exponential function, $\mathrm{i}$: imaginary unit, $\mathbb{Z}$: set of all integers, $\mathrm{Ln}z$: general logarithm function, $k$: integer and $z$: complex variable

A&S Ref:

4.2.2

Permalink:

http://dlmf.nist.gov/4.8.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §4.8(i), §4.8 and Ch.4

►

4.8.9 $$\ln \left(\exp z\right)=z,$$ $-\pi \le \mathrm{\Im }z\le \pi$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function, $\mathrm{\Im }$: imaginary part, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

4.2.3

Permalink:

http://dlmf.nist.gov/4.8.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §4.8(i), §4.8 and Ch.4

►

4.8.10 $$\exp \left(\ln z\right)=\exp \left(\mathrm{Ln}z\right)=z.$$

ⓘ

Symbols:

$\exp z$: exponential function, $\mathrm{Ln}z$: general logarithm function, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

4.2.4

Referenced by:

(25.10.2), §4.8(i)

Permalink:

http://dlmf.nist.gov/4.8.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §4.8(i), §4.8 and Ch.4

… ►

§4.8(ii) Powers

…

29: 10.62 Graphs

§10.62 Graphs

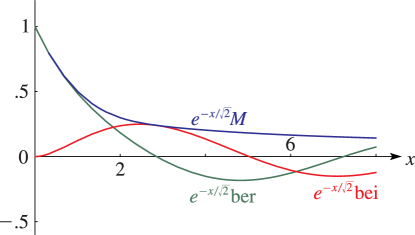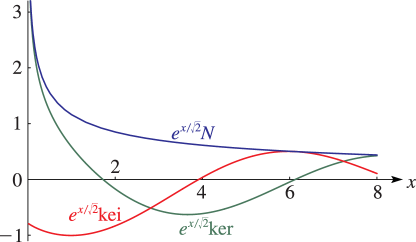►For the modulus functions $M\left(x\right)$ and $N\left(x\right)$ see §10.68(i) with $\nu =0$. … ►

►►

Figure 10.62.3: ${\mathrm{e}}^{-x/\sqrt{2}}\mathrm{ber}x$, ${\mathrm{e}}^{-x/\sqrt{2}}\mathrm{bei}x$, ${\mathrm{e}}^{-x/\sqrt{2}}M\left(x\right)$, $0\le x\le 8$. Magnify

►

►►

Figure 10.62.4: ${\mathrm{e}}^{x/\sqrt{2}}\ker x$, ${\mathrm{e}}^{x/\sqrt{2}}\mathrm{kei}x$, ${\mathrm{e}}^{x/\sqrt{2}}N\left(x\right)$, $0\le x\le 8$. Magnify

30: 7.11 Relations to Other Functions

… ►

Incomplete Gamma Functions and Generalized Exponential Integral

… ►

7.11.3 $$\mathrm{erfc}z=\frac{z}{\sqrt{\pi }}{E}_{\frac{1}{2}}\left(z^2\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{erfc}z$: complementary error function, $E_p\left(z\right)$: generalized exponential integral and $z$: complex variable

Referenced by:

§7.12(i)

Permalink:

http://dlmf.nist.gov/7.11.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §7.11, §7.11 and Ch.7

… ►

7.11.4 $$\mathrm{erf}z=\frac{2z}{\sqrt{\pi }}M(\frac{1}{2},\frac{3}{2},-z^2)=\frac{2z}{\sqrt{\pi }}{\mathrm{e}}^{-z^2}M(1,\frac{3}{2},z^2),$$

ⓘ

Symbols:

$M(a,b,z)$: $={}_1{}^{}F_1^{}(a;b;z)$ Kummer confluent hypergeometric function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{erf}z$: error function, $\mathrm{e}$: base of natural logarithm and $z$: complex variable

A&S Ref:

7.1.21

Permalink:

http://dlmf.nist.gov/7.11.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §7.11, §7.11 and Ch.7

►

7.11.5 $$\mathrm{erfc}z=\frac{1}{\sqrt{\pi }}{\mathrm{e}}^{-z^2}U(\frac{1}{2},\frac{1}{2},z^2)=\frac{z}{\sqrt{\pi }}{\mathrm{e}}^{-z^2}U(1,\frac{3}{2},z^2).$$

ⓘ

Symbols:

$U(a,b,z)$: Kummer confluent hypergeometric function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{erfc}z$: complementary error function, $\mathrm{e}$: base of natural logarithm and $z$: complex variable

Referenced by:

§7.11

Permalink:

http://dlmf.nist.gov/7.11.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §7.11, §7.11 and Ch.7

►

7.11.6 $$C\left(z\right)+\mathrm{i}S\left(z\right)=zM(\frac{1}{2},\frac{3}{2},\frac{1}{2}\pi \mathrm{i}{z}^2)=z{\mathrm{e}}^{\pi \mathrm{i}{z}^2/2}M(1,\frac{3}{2},-\frac{1}{2}\pi \mathrm{i}{z}^2).$$

ⓘ

Symbols:

$C\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $M(a,b,z)$: $={}_1{}^{}F_1^{}(a;b;z)$ Kummer confluent hypergeometric function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit and $z$: complex variable

Permalink:

http://dlmf.nist.gov/7.11.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §7.11, §7.11 and Ch.7

…