Euler%E2%80%93Fermat%20theorem

SearchAdvancedHelp

(0.002 seconds)

21—30 of 503 matching pages

21: Bibliography K

… ►

A proof of the $q$-Macdonald-Morris conjecture for $B{C}_n$ . Mem. Amer. Math. Soc. 108 (516), pp. vi+80.

ⓘ

External Links:

ISSN 0065-9266, MathReview (Eric M. Opdam), ZentralBlatt

Referenced by:

§17.14.

Encodings:

BibTeX

… ►

Linear convergence and the bisection algorithm. Amer. Math. Monthly 93 (1), pp. 48–51.

ⓘ

External Links:

ISSN 0002-9890, FullText, MathReview (J. G. Herriot), ZentralBlatt

Referenced by:

§3.8(iii).

Encodings:

BibTeX

… ►

A general addition theorem for spheroidal wave functions. SIAM J. Math. Anal. 4 (1), pp. 149–160.

ⓘ

External Links:

Document, MathReview (J. Meixner), ZentralBlatt

Referenced by:

§30.10.

Encodings:

BibTeX

… ►

Computation of tangent, Euler, and Bernoulli numbers. Math. Comp. 21 (100), pp. 663–688.

ⓘ

External Links:

FullText, MathReview, ZentralBlatt

Referenced by:

§24.15(ii), §24.19(i).

Encodings:

BibTeX

… ►

A new proof of a Paley-Wiener type theorem for the Jacobi transform. Ark. Mat. 13, pp. 145–159.

ⓘ

External Links:

Document, MathReview (G. Gasper), ZentralBlatt

Referenced by:

§18.10(i).

Encodings:

BibTeX

…

22: 24.20 Tables

§24.20 Tables

… ►Wagstaff (1978) gives complete prime factorizations of $N_n$ and $E_n$ for $n=20(2)60$ and $n=8(2)42$, respectively. …

23: 12.12 Integrals

… ►

12.12.1 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{1}{4}{t}^2}{t}^{\mu -1}U(a,t)dt=\frac{\sqrt{\pi }{2}^{-\frac{1}{2}(\mu +a+\frac{1}{2})}\mathrm{\Gamma }\left(\mu \right)}{\mathrm{\Gamma }\left(\frac{1}{2}(\mu +a+\frac{3}{2})\right)},$$ $\mathrm{\Re }\mu >0$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

►

12.12.2 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{3}{4}{t}^2}{t}^{-a-\frac{3}{2}}U(a,t)dt=2^{\frac{1}{4}+\frac{1}{2}a}\mathrm{\Gamma }\left(-a-\frac{1}{2}\right)\cos \left((\frac{1}{4}a+\frac{1}{8})\pi \right),$$ ,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

►

12.12.3 $${\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\frac{1}{4}{t}^2}{t}^{-a-\frac{1}{2}}{(x^2+t^2)}^{-1}U(a,t)dt=\sqrt{\pi /2}\mathrm{\Gamma }\left(\frac{1}{2}-a\right)x^{-a-\frac{3}{2}}{\mathrm{e}}^{\frac{1}{4}{x}^2}U(-a,x),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $x$: real variable and $a$: real or complex parameter

Permalink:

http://dlmf.nist.gov/12.12.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12 and Ch.12

… ►

12.12.4 $${(U(a,z))}^2+{(\overline{U}(a,z))}^2=\frac{2^{\frac{3}{2}}}{\pi }\mathrm{\Gamma }\left(\frac{1}{2}-a\right){\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{2at+\frac{1}{2}{z}^2\tanh t}}{\sqrt{\sinh \left(2t\right)}}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $\int$: integral, $U(a,z)$: parabolic cylinder function, $\overline{U}(a,x)$: parabolic cylinder function, $\mathrm{\Re }$: real part, $z$: complex variable and $a$: real or complex parameter

Notes:

See Durand (1975).

Referenced by:

§12.12

Permalink:

http://dlmf.nist.gov/12.12.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §12.12, §12.12 and Ch.12

… ►For compendia of integrals see Erdélyi et al. (1953b, v. 2, pp. 121–122), Erdélyi et al. (1954a, b, v. 1, pp. 60–61, 115, 210–211, and 336; v. 2, pp. 76–80, 115, 151, 171, and 395–398), Gradshteyn and Ryzhik (2000, §7.7), Magnus et al. (1966, pp. 330–331), Marichev (1983, pp. 190–191), Oberhettinger (1974, pp. 144–145), Oberhettinger (1990, pp. 106–108 and 192), Oberhettinger and Badii (1973, pp. 181–185), Prudnikov et al. (1986b, pp. 36–37, 155–168, 243–246, 289–290, 327–328, 419–420, and 619), Prudnikov et al. (1992a, §3.11), and Prudnikov et al. (1992b, §3.11). …

24: 5.5 Functional Relations

… ►

5.5.1 $$\mathrm{\Gamma }\left(z+1\right)=z\mathrm{\Gamma }\left(z\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function and $z$: complex variable

A&S Ref:

6.1.15

Referenced by:

§15.4(ii), §15.4(iii), (25.11.27), (25.5.6), §5.4(i)

Permalink:

http://dlmf.nist.gov/5.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §5.5(i), §5.5 and Ch.5

… ►

5.5.3 $$\mathrm{\Gamma }\left(z\right)\mathrm{\Gamma }\left(1-z\right)=\pi /\sin \left(\pi z\right),$$ $z\ne 0,\pm 1,\mathrm{\dots }$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\sin z$: sine function and $z$: complex variable

A&S Ref:

6.1.17 (without the condition on $z$.)

Referenced by:

§10.19(i), §15.4(ii), §15.8(ii), (25.9.2), §5.21, (9.10.18), (9.12.15)

Permalink:

http://dlmf.nist.gov/5.5.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §5.5(ii), §5.5 and Ch.5

… ►

5.5.5 $$\mathrm{\Gamma }\left(2z\right)={\pi }^{-1/2}{2}^{2z-1}\mathrm{\Gamma }\left(z\right)\mathrm{\Gamma }\left(z+\frac{1}{2}\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter and $z$: complex variable

A&S Ref:

6.1.18

Referenced by:

§14.19(ii), §15.4(i), §15.4(iii), (25.9.2), §5.5(iii)

Permalink:

http://dlmf.nist.gov/5.5.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §5.5(iii), §5.5(iii), §5.5 and Ch.5

… ►

§5.5(iv) Bohr–Mollerup Theorem

►If a positive function $f(x)$ on $(0,\mathrm{\infty })$ satisfies $f(x+1)=xf(x)$, $f(1)=1$, and $\ln f(x)$ is convex (see §1.4(viii)), then $f(x)=\mathrm{\Gamma }\left(x\right)$.

25: 27.4 Euler Products and Dirichlet Series

§27.4 Euler Products and Dirichlet Series

►The fundamental theorem of arithmetic is linked to analysis through the concept of the Euler product. …In this case the infinite product on the right (extended over all primes $p$) is also absolutely convergent and is called the Euler product of the series. If $f(n)$ is completely multiplicative, then each factor in the product is a geometric series and the Euler product becomes … ►Euler products are used to find series that generate many functions of multiplicative number theory. …

26: 27.8 Dirichlet Characters

… ►For any character $\chi (modk)$, $\chi \left(n\right)\ne 0$ if and only if $\left(n,k\right)=1$, in which case the Euler–Fermat theorem (27.2.8) implies ${\left(\chi \left(n\right)\right)}^{\varphi \left(k\right)}=1$. There are exactly $\varphi \left(k\right)$ different characters (mod $k$), which can be labeled as ${\chi }_1,\mathrm{\dots },{\chi }_{\varphi \left(k\right)}$. … ►

27.8.6

ⓘ

Symbols:

$\chi \left(n\right)$: Dirichlet character, $\varphi \left(n\right)$: Euler’s totient, $\overline{z}$: complex conjugate, $\equiv$: modular equivalence, $k$: positive integer, $m$: positive integer and $n$: positive integer

Permalink:

http://dlmf.nist.gov/27.8.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §27.8 and Ch.27

…

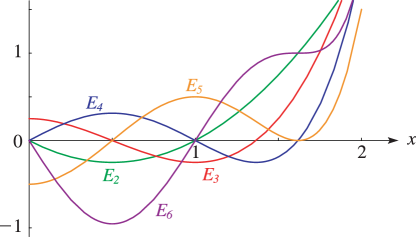
27: 24.3 Graphs

… ►

►►

Figure 24.3.2: Euler polynomials $E_n\left(x\right)$, $n=2,3,\mathrm{\dots },6$. Magnify

28: 5.11 Asymptotic Expansions

… ►The scaled gamma function ${\mathrm{\Gamma }}^{\ast }\left(z\right)$ is defined in (5.11.3) and its main property is ${\mathrm{\Gamma }}^{\ast }\left(z\right)\sim 1$ as $z\to \mathrm{\infty }$ in the sector $|\mathrm{ph}z|\le \pi -\delta$. Wrench (1968) gives exact values of $g_k$ up to $g_{20}$. … ►

5.11.12 $$\frac{\mathrm{\Gamma }\left(z+a\right)}{\mathrm{\Gamma }\left(z+b\right)}\sim z^{a-b},$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\sim$: asymptotic equality, $z$: complex variable, $a$: real or complex variable and $b$: real or complex variable

Referenced by:

§5.11(i)

Permalink:

http://dlmf.nist.gov/5.11.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §5.11(iii), §5.11 and Ch.5

►

5.11.13 $$\frac{\mathrm{\Gamma }\left(z+a\right)}{\mathrm{\Gamma }\left(z+b\right)}\sim z^{a-b}\sum _{k=0}^{\mathrm{\infty }}\frac{G_k(a,b)}{z^k},$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\sim$: Poincaré asymptotic expansion, $k$: nonnegative integer, $z$: complex variable, $a$: real or complex variable, $b$: real or complex variable and $G_k(a,b)$: coefficients

A&S Ref:

6.1.47

Permalink:

http://dlmf.nist.gov/5.11.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §5.11(iii), §5.11 and Ch.5

… ►

5.11.19 $$\frac{\mathrm{\Gamma }\left(z+a\right)\mathrm{\Gamma }\left(z+b\right)}{\mathrm{\Gamma }\left(z+c\right)}\sim \sum _{k=0}^{\mathrm{\infty }}{(-1)}^k\frac{{\left(c-a\right)}_k{\left(c-b\right)}_k}{k!}\mathrm{\Gamma }\left(a+b-c+z-k\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\sim$: Poincaré asymptotic expansion, $!$: factorial (as in $n!$), $k$: nonnegative integer, $z$: complex variable, $a$: real or complex variable and $b$: real or complex variable

Referenced by:

§5.11(i), §5.11(iii)

Permalink:

http://dlmf.nist.gov/5.11.E19

Encodings:

pMML, png, TeX

See also:

Annotations for §5.11(iii), §5.11 and Ch.5

…

29: 8.15 Sums

… ►

8.15.1 $$\gamma (a,\lambda x)={\lambda }^a\sum _{k=0}^{\mathrm{\infty }}\gamma (a+k,x)\frac{{(1-\lambda )}^k}{k!}.$$

ⓘ

Symbols:

$!$: factorial (as in $n!$), $\gamma (a,z)$: incomplete gamma function, $x$: real variable, $a$: parameter and $k$: nonnegative integer

Permalink:

http://dlmf.nist.gov/8.15.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §8.15 and Ch.8

►

8.15.2 $$a\sum _{k=1}^{\mathrm{\infty }}\left(\frac{{\mathrm{e}}^{2\pi \mathrm{i}k(z+h)}}{{\left(2\pi \mathrm{i}k\right)}^{a+1}}\mathrm{\Gamma }(a,2\pi \mathrm{i}kz)+\frac{{\mathrm{e}}^{-2\pi \mathrm{i}k(z+h)}}{{\left(-2\pi \mathrm{i}k\right)}^{a+1}}\mathrm{\Gamma }(a,-2\pi \mathrm{i}kz)\right)=\zeta (-a,z+h)+\frac{z^{a+1}}{a+1}+\left(h-\frac{1}{2}\right)z^a,$$ $h\in [0,1]$.

ⓘ

Symbols:

$\zeta (s,a)$: Hurwitz zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $[a,b]$: closed interval, $\in$: element of, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{\Gamma }(a,z)$: incomplete gamma function, $z$: complex variable, $a$: parameter and $k$: nonnegative integer

Proof sketch:

Start with and $z>0$. For $\mathrm{\Gamma }(a,\pm 2\pi \mathrm{i}kz)$ take integral representation (8.2.2) and use the substitution $t=\pm 2\pi \mathrm{i}kz(1+\tau )$. The sum and the integral can be interchanged, and the sum can be evaluated via (4.6.1). Use integration by parts. This will result in $\left(h-\frac{1}{2}\right)z^a$ plus two integrals with infinitely many poles. The residue theorem (§1.10(iv)) will give us an infinite series which can be identified via (25.11.1). For other values of $a$ and $z$ use analytic continuation.

Referenced by:

§25.11(x), §25.11(x), §8.15, Erratum (V1.1.3) for Additions

Permalink:

http://dlmf.nist.gov/8.15.E2

Encodings:

pMML, png, TeX

Addition (effective with 1.1.3):

This equation was added.

See also:

Annotations for §8.15 and Ch.8

…

30: 10.44 Sums

… ►

§10.44(i) Multiplication Theorem

… ►

§10.44(ii) Addition Theorems

►

Neumann’s Addition Theorem

… ►

Graf’s and Gegenbauer’s Addition Theorems

… ►where $\gamma$ is Euler’s constant and $\psi ={\mathrm{\Gamma }}^{\prime }/\mathrm{\Gamma }$ (§5.2). …