哪里能办理阿联酋身份证KYC认证资料〖办证V信ATV1819〗4Cd

SearchAdvancedHelp

(0.003 seconds)

11—20 of 524 matching pages

11: Bibliography T

… ►

Zonal Polynomials. Institute of Mathematical Statistics Lecture Notes—Monograph Series, 4, Institute of Mathematical Statistics, Hayward, CA.

ⓘ

External Links:

ISBN 0-940600-05-6, FullText, MathReview (A. W. Davis), ZentralBlatt

Referenced by:

§35.4(i), §35.9.

Encodings:

BibTeX

… ►

The asymptotic expansion of the incomplete gamma functions. SIAM J. Math. Anal. 10 (4), pp. 757–766.

ⓘ

External Links:

ISSN 0036-1410, Document, MathReview (E. Riekstiņš), ZentralBlatt

Referenced by:

§8.12.

Encodings:

BibTeX

… ►

Atlas for Computing Mathematical Functions: An Illustrated Guide for Practitioners. John Wiley & Sons Inc., New York.

ⓘ

Notes:

With CD-ROM containing a large collection of mathematical function software written in Fortran 90 and Mathematica (an edition with the same software in C and Mathematica exists also). The functions are computed for real variables only. Maximum accuracy 12D.

External Links:

ISBN 0-471-18171-4, MathReview, ZentralBlatt

Referenced by:

§19.36(ii), § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index, § ‣ Software Cross Index.

Encodings:

BibTeX

… ►

Sul comportamento asintotico dell’$n$-esimo polinomio di Laguerre nell’intorno dell’ascissa $4n$ . Comment. Math. Helv. 22, pp. 150–167.

ⓘ

External Links:

ISSN 0010-2571, Document, MathReview (G. Szegő), ZentralBlatt

Referenced by:

§18.16(iv).

Encodings:

BibTeX

… ►

Theory of the Fresnel integral. USSR Comput. Math. and Math. Phys. 9 (4), pp. 271–279.

ⓘ

Notes:

Translation of the paper in Zh. Vychisl. Mat. Mat. Fiz., Vol. 9, No. 4, 938-944, 1969

External Links:

Document, ZentralBlatt

Referenced by:

§7.13(iv).

Encodings:

BibTeX

12: 22.17 Moduli Outside the Interval [0,1]

… ►

22.17.7 $$\mathrm{cn}(z,\mathrm{i}k)=\mathrm{cd}(z/k_1^{\prime },k_1),$$

ⓘ

Symbols:

$\mathrm{cd}(z,k)$: Jacobian elliptic function, $\mathrm{cn}(z,k)$: Jacobian elliptic function, $\mathrm{i}$: imaginary unit, $z$: complex, $k$: modulus, $k_1$: change of variable and $k_1^{\prime }$: change of variable

A&S Ref:

16.10.3 (modified)

Permalink:

http://dlmf.nist.gov/22.17.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §22.17(i), §22.17 and Ch.22

…

13: Errata

… ►

22.9.8 $$s_{1,3}^{(4)}{s}_{2,3}^{(4)}+s_{2,3}^{(4)}{s}_{3,3}^{(4)}+s_{3,3}^{(4)}{s}_{1,3}^{(4)}=\frac{{\kappa }^2-1}{k^2}$$

22.9.9 $$c_{1,3}^{(4)}{c}_{2,3}^{(4)}+c_{2,3}^{(4)}{c}_{3,3}^{(4)}+c_{3,3}^{(4)}{c}_{1,3}^{(4)}=-\frac{\kappa (\kappa +2)}{{(1+\kappa )}^2}$$

22.9.10 $$d_{1,3}^{(2)}{d}_{2,3}^{(2)}+d_{2,3}^{(2)}{d}_{3,3}^{(2)}+d_{3,3}^{(2)}{d}_{1,3}^{(2)}=d_{1,3}^{(4)}{d}_{2,3}^{(4)}+d_{2,3}^{(4)}{d}_{3,3}^{(4)}+d_{3,3}^{(4)}{d}_{1,3}^{(4)}=\kappa (\kappa +2)$$

Originally all the functions $s_{m,p}^{(4)}$, $c_{m,p}^{(4)}$ , $d_{m,p}^{(2)}$ and $d_{m,p}^{(4)}$ in Equations (22.9.8), (22.9.9) and (22.9.10) were written incorrectly with $p=2$. These functions have been corrected so that they are written with $p=3$. In the sentence just below (22.9.10), the expression $s_{m,2}^{(4)}{s}_{n,2}^{(4)}$ has been corrected to read $s_{m,p}^{(4)}{s}_{n,p}^{(4)}$.

Reported by Juan Miguel Nieto on 2019-11-07

… ►

Originally a minus sign was missing in the entries for $\mathrm{cd}u$ and $\mathrm{dc}u$ in the second column (headed $z+K+i{K}^{\prime }$). The correct entries are $-k^{-1}\mathrm{ns}z$ and $-k\mathrm{sn}z$. Note: These entries appear online but not in the published print edition. More specifically, Table 22.4.3 in the published print edition is restricted to the three Jacobian elliptic functions $\mathrm{sn},\mathrm{cn},\mathrm{dn}$, whereas Table 22.4.3 covers all 12 Jacobian elliptic functions.

	$u$
	$z+K$	$z+K+\mathrm{i}{K}^{\prime }$	$z+\mathrm{i}{K}^{\prime }$	$z+2K$	$z+2K+2\mathrm{i}{K}^{\prime }$	$z+2\mathrm{i}{K}^{\prime }$
$\mathrm{⋮}$
$\mathrm{cd}u$	$-\mathrm{sn}z$	$-k^{-1}\mathrm{ns}z$	$k^{-1}\mathrm{dc}z$	$-\mathrm{cd}z$	$-\mathrm{cd}z$	$\mathrm{cd}z$
$\mathrm{⋮}$
$\mathrm{dc}u$	$-\mathrm{ns}z$	$-k\mathrm{sn}z$	$k\mathrm{cd}z$	$-\mathrm{dc}z$	$-\mathrm{dc}z$	$\mathrm{dc}z$
$\mathrm{⋮}$

Reported 2014-02-28 by Svante Janson.

… ►

13.18.7 $$W_{-\frac{1}{4},\pm \frac{1}{4}}\left(z^2\right)={\mathrm{e}}^{\frac{1}{2}{z}^2}\sqrt{\pi z}\mathrm{erfc}\left(z\right)$$

Originally the left-hand side was given correctly as $W_{-\frac{1}{4},-\frac{1}{4}}\left(z^2\right)$; the equation is true also for $W_{-\frac{1}{4},+\frac{1}{4}}\left(z^2\right)$.

… ►

Originally the ordinate labels 2 and 4 in this figure were placed too high.

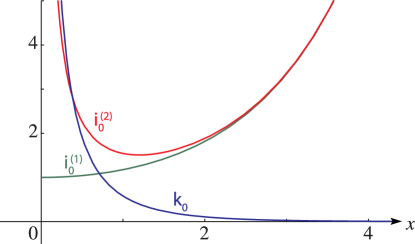
Reported 2010-11-08 by Wolfgang Ehrhardt.

… ►

Originally the limiting form for $\mathrm{sc}(z,k)$ in the last line of this table was incorrect ($\cosh z$, instead of $\sinh z$).

$\mathrm{sn}(z,k)$ $\to$	$\tanh z$	$\mathrm{cd}(z,k)$ $\to$	$1$	$\mathrm{dc}(z,k)$ $\to$	$1$	$\mathrm{ns}(z,k)$ $\to$	$\coth z$
$\mathrm{cn}(z,k)$ $\to$	$\mathrm{sech}z$	$\mathrm{sd}(z,k)$ $\to$	$\sinh z$	$\mathrm{nc}(z,k)$ $\to$	$\cosh z$	$\mathrm{ds}(z,k)$ $\to$	$\mathrm{csch}z$
$\mathrm{dn}(z,k)$ $\to$	$\mathrm{sech}z$	$\mathrm{nd}(z,k)$ $\to$	$\cosh z$	$\mathrm{sc}(z,k)$ $\to$	$\sinh z$	$\mathrm{cs}(z,k)$ $\to$	$\mathrm{csch}z$

Reported 2010-11-23.

…

14: 22.5 Special Values

… ►

Table 22.5.1: Jacobian elliptic function values, together with derivatives or residues, for special values of the variable.

► ►►►

	$z$
…
$\mathrm{cd}z$	$1,0$	$0,-1$	$\mathrm{\infty },-k^{-1}$	$k^{-1},0$	$-1,0$	$-1,0$	$1,0$
…

►

… ►

Table 22.5.3: Limiting forms of Jacobian elliptic functions as $k\to 0$.

► ►►

$\mathrm{sn}(z,k)$ $\to$	$\sin z$	$\mathrm{cd}(z,k)$ $\to$	$\cos z$	$\mathrm{dc}(z,k)$ $\to$	$\sec z$	$\mathrm{ns}(z,k)$ $\to$	$\csc z$
…

►

►

Table 22.5.4: Limiting forms of Jacobian elliptic functions as $k\to 1$.

► ►►

$\mathrm{sn}(z,k)$ $\to$	$\tanh z$	$\mathrm{cd}(z,k)$ $\to$	$1$	$\mathrm{dc}(z,k)$ $\to$	$1$	$\mathrm{ns}(z,k)$ $\to$	$\coth z$
…

►

…

15: Bibliography L

… ►

A Numerical Library in Java for Scientists & Engineers. Chapman & Hall/CRC, Boca Raton, FL.

ⓘ

Notes:

With 1 CD-ROM (Windows, Macintosh and Unix) containing a large general purpose mathematical software collection written in Java including a collection of special function classes. The functions are computed for real variables only. (See Lau (1995) for C version).

External Links:

ISBN 1-58488-430-4, MathReview Entry, ZentralBlatt

Referenced by:

H. T. Lau (1995).

Encodings:

BibTeX

… ►

A partition function connected with the modulus five. Duke Math. J. 8 (4), pp. 631–655.

ⓘ

External Links:

Document, MathReview (R. D. James), ZentralBlatt

Referenced by:

§17.18.

Encodings:

BibTeX

… ►

Zur Theorie der Gaußschen Summen. Math. Ann. 57 (4), pp. 554–567 (German).

ⓘ

External Links:

ISSN 0025-5831, Document, MathReview Entry, ZentralBlatt

Referenced by:

§20.11(i).

Encodings:

BibTeX

… ►

Uniform asymptotic expansions of symmetric elliptic integrals. Constr. Approx. 17 (4), pp. 535–559.

ⓘ

External Links:

ISSN 0176-4276, Document, MathReview (Valdir A. Menegatto), ZentralBlatt

Referenced by:

§19.27(vi).

Encodings:

BibTeX

… ►

Solutions of the fifth Painlevé equation. Differ. Uravn. 4 (8), pp. 1413–1420 (Russian).

ⓘ

Notes:

In Russian. English translation: Differential Equations 4(8), pp. 732–735

External Links:

MathReview (C. E. Langenhop), ZentralBlatt

Referenced by:

§32.10(v), §32.8(v).

Encodings:

BibTeX

…

16: 22.1 Special Notation

… ►The functions treated in this chapter are the three principal Jacobian elliptic functions $\mathrm{sn}(z,k)$, $\mathrm{cn}(z,k)$, $\mathrm{dn}(z,k)$; the nine subsidiary Jacobian elliptic functions $\mathrm{cd}(z,k)$, $\mathrm{sd}(z,k)$, $\mathrm{nd}(z,k)$, $\mathrm{dc}(z,k)$, $\mathrm{nc}(z,k)$, $\mathrm{sc}(z,k)$, $\mathrm{ns}(z,k)$, $\mathrm{ds}(z,k)$, $\mathrm{cs}(z,k)$; the amplitude function $\mathrm{am}(x,k)$; Jacobi’s epsilon and zeta functions $ℰ(x,k)$ and $\mathrm{Z}\left(x|k\right)$. …

17: Bibliography B

… ►

A new method for investigating Euler sums. Ramanujan J. 4 (4), pp. 397–419.

ⓘ

External Links:

ISSN 1382-4090, Document, MathReview (Bruce C. Berndt), ZentralBlatt

Referenced by:

(25.6.16), (25.6.17), (25.6.18), (25.6.19), (25.6.20), §25.6(iii), §25.6(iii), §25.6.

Encodings:

BibTeX

… ►

Asymptotic methods in enumeration. SIAM Rev. 16 (4), pp. 485–515.

ⓘ

External Links:

Document, MathReview (Bernard Harris), ZentralBlatt

Referenced by:

Ch.2.

Encodings:

BibTeX

… ►

A uniform asymptotic formula for orthogonal polynomials associated with $\exp (-x^4)$ . J. Approx. Theory 98, pp. 146–166.

ⓘ

External Links:

ISSN 0021-9045, Document, MathReview (V. L. Deshpande), ZentralBlatt

Referenced by:

§18.32.

Encodings:

BibTeX

… ►

Constant mean curvature surfaces and integrable equations. Uspekhi Mat. Nauk 46 (4(280)), pp. 3–42, 192 (Russian).

ⓘ

Notes:

In Russian. English translation: Russian Math. Surveys, 46(1991), no. 4, pp. 1–45

External Links:

ISSN 0042-1316, MathReview (P. E. Markov), ZentralBlatt

Referenced by:

§32.11(iv).

Encodings:

BibTeX

… ►

A Course in Computational Number Theory. Key College Publishing, Emeryville, CA.

ⓘ

Notes:

With 1 CD-ROM (Windows, Macintosh and UNIX) containing a collection of Mathematica programs for computations in number theory.

External Links:

ISBN 1-930190-10-7, MathReview (Samuel S. Wagstaff, Jr.), ZentralBlatt

Referenced by:

§27.12, §27.19, §27.21, 2nd item, Profile David M. Bressoud.

Encodings:

BibTeX

…

18: 4 Elementary Functions

Chapter 4 Elementary Functions

…

19: 22.9 Cyclic Identities

… ►These identities are cyclic in the sense that each of the indices $m,n$ in the first product of, for example, the form $s_{m,p}^{(4)}{s}_{n,p}^{(4)}$ are simultaneously permuted in the cyclic order: $m\to m+1\to m+2\to \mathrm{\cdots }p\to 1\to 2\to \mathrm{\cdots }m-1$; $n\to n+1\to n+2\to \mathrm{\cdots }p\to 1\to 2\to \mathrm{\cdots }n-1$. … ►

22.9.17 $$d_{1,4}^{(2)}{d}_{2,4}^{(2)}{d}_{3,4}^{(2)}\pm d_{2,4}^{(2)}{d}_{3,4}^{(2)}{d}_{4,4}^{(2)}+d_{3,4}^{(2)}{d}_{4,4}^{(2)}{d}_{1,4}^{(2)}\pm d_{4,4}^{(2)}{d}_{1,4}^{(2)}{d}_{2,4}^{(2)}=k^{\prime }\left(\pm d_{1,4}^{(2)}+d_{2,4}^{(2)}\pm d_{3,4}^{(2)}+d_{4,4}^{(2)}\right),$$

ⓘ

Symbols:

$k^{\prime }$: complementary modulus and $d_{m,p}^{(r)}$: cyclic quantity

Permalink:

http://dlmf.nist.gov/22.9.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §22.9(iii), §22.9(iii), §22.9 and Ch.22

►

22.9.18 $${\left(d_{1,4}^{(2)}\right)}^2{d}_{3,4}^{(2)}\pm {\left(d_{2,4}^{(2)}\right)}^2{d}_{4,4}^{(2)}+{\left(d_{3,4}^{(2)}\right)}^2{d}_{1,4}^{(2)}\pm {\left(d_{4,4}^{(2)}\right)}^2{d}_{2,4}^{(2)}=k^{\prime }\left(d_{1,4}^{(2)}\pm d_{2,4}^{(2)}+d_{3,4}^{(2)}\pm d_{4,4}^{(2)}\right),$$

ⓘ

Symbols:

$k^{\prime }$: complementary modulus and $d_{m,p}^{(r)}$: cyclic quantity

Permalink:

http://dlmf.nist.gov/22.9.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §22.9(iii), §22.9(iii), §22.9 and Ch.22

… ►

§22.9(iv) Typical Identities of Rank 4

… ►

22.9.23 $$s_{1,3}^{(4)}{d}_{1,3}^{(4)}{c}_{2,3}^{(4)}{c}_{3,3}^{(4)}+s_{2,3}^{(4)}{d}_{2,3}^{(4)}{c}_{3,3}^{(4)}{c}_{1,3}^{(4)}+s_{3,3}^{(4)}{d}_{3,3}^{(4)}{c}_{1,3}^{(4)}{c}_{2,3}^{(4)}=\frac{{\kappa }^2}{1-{\kappa }^2}\left(s_{1,3}^{(4)}{d}_{1,3}^{(4)}+s_{2,3}^{(4)}{d}_{2,3}^{(4)}+s_{2,3}^{(4)}{d}_{2,3}^{(4)}\right).$$

ⓘ

Symbols:

$s_{m,p}^{(r)}$: cyclic quantity, $c_{m,p}^{(r)}$: cyclic quantity, $d_{m,p}^{(r)}$: cyclic quantity and $\kappa$: change of variable

Permalink:

http://dlmf.nist.gov/22.9.E23

Encodings:

pMML, png, TeX

See also:

Annotations for §22.9(iv), §22.9(iv), §22.9 and Ch.22

…

20: 22.12 Expansions in Other Trigonometric Series and Doubly-Infinite Partial Fractions: Eisenstein Series

… ►

22.12.5 $$2Kk\mathrm{cd}(2Kt,k)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\pi }{\sin \left(\pi (t+\frac{1}{2}-(n+\frac{1}{2})\tau )\right)}=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\left(\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{{(-1)}^m}{t+\frac{1}{2}-m-(n+\frac{1}{2})\tau }\right),$$

ⓘ

Symbols:

$\mathrm{cd}(z,k)$: Jacobian elliptic function, $\pi$: the ratio of the circumference of a circle to its diameter, $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $\sin z$: sine function, $k$: modulus and $\tau$: ratio

Referenced by:

§22.12

Permalink:

http://dlmf.nist.gov/22.12.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §22.12 and Ch.22

…