spheroidal wave functions

SearchAdvancedHelp

(0.003 seconds)

1—10 of 37 matching pages

1: 30.1 Special Notation

… ►The main functions treated in this chapter are the eigenvalues ${\lambda }_n^m\left({\gamma }^2\right)$ and the spheroidal wave functions ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$, ${\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2)$, ${\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)$, and $S_n^{m(j)}(z,\gamma )$, $j=1,2,3,4$. …Meixner and Schäfke (1954) use $\mathrm{ps}$, $\mathrm{qs}$, $\mathrm{Ps}$, $\mathrm{Qs}$ for $\mathrm{𝖯𝗌}$, $\mathrm{𝖰𝗌}$, $\mathrm{𝑃𝑠}$, $\mathrm{𝑄𝑠}$, respectively. ►

Other Notations

►Flammer (1957) and Abramowitz and Stegun (1964) use ${\lambda }_{mn}(\gamma )$ for ${\lambda }_n^m\left({\gamma }^2\right)+{\gamma }^2$, $R_{mn}^{(j)}(\gamma ,z)$ for $S_n^{m(j)}(z,\gamma )$, and …

2: 30.11 Radial Spheroidal Wave Functions

§30.11 Radial Spheroidal Wave Functions

►

§30.11(i) Definitions

… ►

Connection Formulas

… ►

►►

Figure 30.11.4: $S_n^{1(1)}(\mathrm{i}y,2\mathrm{i})$, $n=1,2$, $0\le y\le 10$. Magnify

… ►

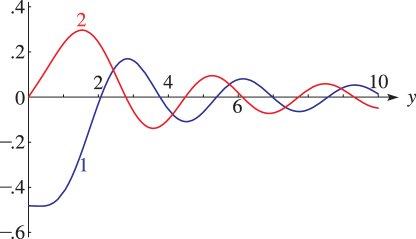§30.11(v) Connection with the $\mathrm{𝑃𝑠}$ and $\mathrm{𝑄𝑠}$ Functions

…

3: 30.10 Series and Integrals

… ►

4: 30 Spheroidal Wave Functions

Chapter 30 Spheroidal Wave Functions

…

5: 30.12 Generalized and Coulomb Spheroidal Functions

§30.12 Generalized and Coulomb Spheroidal Functions

►Generalized spheroidal wave functions and Coulomb spheroidal functions are solutions of the differential equation …

6: 30.5 Functions of the Second Kind

§30.5 Functions of the Second Kind

… ►

30.5.1 $${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2),$$ $n=m,m+1,m+2,\mathrm{\dots }$.

ⓘ

Symbols:

${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.5.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §30.5 and Ch.30

… ►

30.5.2 $${\mathrm{𝖰𝗌}}_n^m(-x,{\gamma }^2)={(-1)}^{n-m+1}{\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2),$$

ⓘ

Symbols:

${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.5.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §30.5 and Ch.30

… ►

30.5.3 $${\mathrm{𝖰𝗌}}_n^m(x,0)={𝖰}_n^m\left(x\right);$$

ⓘ

Symbols:

: Ferrers function of the second kind, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer and $n\ge m$: integer degree

Permalink:

http://dlmf.nist.gov/30.5.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §30.5 and Ch.30

… ►

30.5.4 $$𝒲\left\{{\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2),{\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)\right\}=\frac{(n+m)!}{(1-x^2)(n-m)!}{A}_n^m({\gamma }^2)A_n^{-m}({\gamma }^2)(\ne 0),$$

ⓘ

Symbols:

$𝒲$: Wronskian, $!$: factorial (as in $n!$), ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree, $A_n^m({\gamma }^2)$ and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.5.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §30.5 and Ch.30

…

7: 30.6 Functions of Complex Argument

§30.6 Functions of Complex Argument

►The solutions … ►

30.6.4 $${\mathrm{𝑃𝑠}}_n^m(x\pm \mathrm{i}0,{\gamma }^2)={(\mp \mathrm{i})}^m{\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2),$$

ⓘ

Symbols:

$\mathrm{i}$: imaginary unit, ${\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2)$: spheroidal wave function of complex argument, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.6.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §30.6, §30.6 and Ch.30

►

30.6.5 $${\mathrm{𝑄𝑠}}_n^m(x\pm \mathrm{i}0,{\gamma }^2)={(\mp \mathrm{i})}^m\left({\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)\mp \frac{1}{2}\mathrm{i}\pi {\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{i}$: imaginary unit, ${\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)$: spheroidal wave function of complex argument, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.6.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §30.6, §30.6 and Ch.30

… ►

8: 30.4 Functions of the First Kind

§30.4 Functions of the First Kind

►

§30.4(i) Definitions

… ►If $\gamma =0$, ${\mathrm{𝖯𝗌}}_n^m(x,0)$ reduces to the Ferrers function ${𝖯}_n^m\left(x\right)$: … ►

§30.4(ii) Elementary Properties

… ►

§30.4(iv) Orthogonality

…

9: Hans Volkmer

… ►Hans Volkmer is the author of DLMF Chapters 29 Lamé Functions, 30 Spheroidal Wave Functions. … ►

30 Spheroidal Wave Functions

…

10: 30.15 Signal Analysis

§30.15 Signal Analysis

►

§30.15(i) Scaled Spheroidal Wave Functions

… ►

§30.15(ii) Integral Equation

… ► … ►