radial spheroidal wave functions

SearchAdvancedHelp

(0.004 seconds)

1—10 of 13 matching pages

1: 30.11 Radial Spheroidal Wave Functions

§30.11 Radial Spheroidal Wave Functions

►

§30.11(i) Definitions

… ►

Connection Formulas

… ►

►►

Figure 30.11.4: $S_n^{1(1)}(\mathrm{i}y,2\mathrm{i})$, $n=1,2$, $0\le y\le 10$. Magnify

… ►

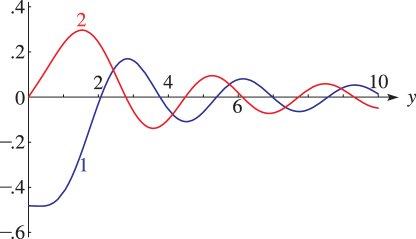§30.11(v) Connection with the $\mathrm{𝑃𝑠}$ and $\mathrm{𝑄𝑠}$ Functions

…

2: 30.16 Methods of Computation

… ►

§30.16(iii) Radial Spheroidal Wave Functions

…

3: 30.17 Tables

§30.17 Tables

…

4: 30.14 Wave Equation in Oblate Spheroidal Coordinates

… ►

30.14.8 $$w_1(\xi )=a_1{S}_n^{m(1)}(\mathrm{i}\xi ,\gamma )+b_1{S}_n^{m(2)}(\mathrm{i}\xi ,\gamma ).$$

ⓘ

Symbols:

$\mathrm{i}$: imaginary unit, $S_n^{m(j)}(z,\gamma )$: radial spheroidal wave function, $m$: nonnegative integer, $n\ge m$: integer degree, $b_j$: coefficients, $a_j$: coefficients, $\xi$: oblate spheroidal coordinate, $w_j$: solution to DE and ${\gamma }^2={\kappa }^2{c}^2$: parameter

Referenced by:

§30.14(v)

Permalink:

http://dlmf.nist.gov/30.14.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §30.14(iv), §30.14 and Ch.30

… ►

§30.14(v) The Interior Dirichlet Problem for Oblate Ellipsoids

… ►

30.14.9 $$S_n^{m(1)}(\mathrm{i}{\xi }_0,\gamma )=0.$$

ⓘ

Symbols:

$\mathrm{i}$: imaginary unit, $S_n^{m(j)}(z,\gamma )$: radial spheroidal wave function, $m$: nonnegative integer, $n\ge m$: integer degree, $\xi$: oblate spheroidal coordinate and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.14.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §30.14(v), §30.14 and Ch.30

…

5: 30.1 Special Notation

… ►The main functions treated in this chapter are the eigenvalues ${\lambda }_n^m\left({\gamma }^2\right)$ and the spheroidal wave functions ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$, ${\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2)$, ${\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)$, and $S_n^{m(j)}(z,\gamma )$, $j=1,2,3,4$. … ►Flammer (1957) and Abramowitz and Stegun (1964) use ${\lambda }_{mn}(\gamma )$ for ${\lambda }_n^m\left({\gamma }^2\right)+{\gamma }^2$, $R_{mn}^{(j)}(\gamma ,z)$ for $S_n^{m(j)}(z,\gamma )$, and …

6: 30.13 Wave Equation in Prolate Spheroidal Coordinates

… ►

30.13.14 $$w_1(\xi )=a_1{S}_n^{m(1)}(\xi ,\gamma )+b_1{S}_n^{m(2)}(\xi ,\gamma ).$$

ⓘ

Symbols:

$S_n^{m(j)}(z,\gamma )$: radial spheroidal wave function, $m$: nonnegative integer, $n\ge m$: integer degree, $\xi$: prolate spheroidal coordinate, $b_j$: coefficients, $w_j$: solution to DE, ${\gamma }^2={\kappa }^2{c}^2$: parameter and $a_j$: coefficients

Referenced by:

§30.13(v)

Permalink:

http://dlmf.nist.gov/30.13.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §30.13(iv), §30.13 and Ch.30

… ►

30.13.15 $$S_n^{m(1)}({\xi }_0,\gamma )=0.$$

ⓘ

Symbols:

$S_n^{m(j)}(z,\gamma )$: radial spheroidal wave function, $m$: nonnegative integer, $n\ge m$: integer degree, $\xi$: prolate spheroidal coordinate and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.13.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §30.13(v), §30.13 and Ch.30

…

7: Bibliography H

… ►

Tables of Radial Spheroidal Wave Functions, Vols. 1-3, Prolate, $m=0,1,2$; Vols. 4-6, Oblate, $m=0,1,2$ . Technical report Naval Research Laboratory, Washington, D.C..

ⓘ

Notes:

NRL Reports 7088-7093

External Links:

ZentralBlatt

Referenced by:

3rd item.

Encodings:

BibTeX

…

8: Bibliography B

… ►

Prolate radial spheroidal wave functions. Comput. Phys. Comm. 30 (2), pp. 177–185.

ⓘ

External Links:

Document, Code

Referenced by:

1st item.

Encodings:

BibTeX

…

9: Bibliography C

… ►

Product formulas and convolutions for angular and radial spheroidal wave functions. Trans. Amer. Math. Soc. 338 (2), pp. 695–710.

ⓘ

External Links:

ISSN 0002-9947, FullText, MathReview (Jean-Claude Lucquiaud), ZentralBlatt

Referenced by:

§30.10, §30.11(vi).

Encodings:

BibTeX

…

10: Bibliography V

… ►

Calculation of spheroidal wave functions. J. Acoust. Soc. Amer. 51, pp. 414–416.

ⓘ

External Links:

Document, ZentralBlatt

Referenced by:

§30.16(ii), §30.18(iii).

Encodings:

BibTeX

►

A Fortran computer program for calculating the oblate spheroidal radial functions of the first and second kind and their first derivatives. NRL Report No. 6959 Naval Res. Lab.  Washingtion, D.C..

ⓘ

Referenced by:

§30.18(iii).

Encodings:

BibTeX

… ►

Accurate calculation of prolate spheroidal radial functions of the first kind and their first derivatives. Quart. Appl. Math. 60 (3), pp. 589–599.

ⓘ

Notes:

For software, see Van Buren (website)

External Links:

ISSN 0033-569X, MathReview (Alan M. Cohen), ZentralBlatt

Referenced by:

§30.16(iii).

Encodings:

BibTeX

►

Improved calculation of prolate spheroidal radial functions of the second kind and their first derivatives. Quart. Appl. Math. 62 (3), pp. 493–507.

ⓘ

Notes:

For software, see Van Buren (website)

External Links:

ISSN 0033-569X, FullText, MathReview (Javier Segura), ZentralBlatt

Referenced by:

§30.16(iii), §30.16(iii).

Encodings:

BibTeX

… ►

Mathieu and Spheroidal Wave Functions: Fortran Programs for their Accurate Calculation

ⓘ

External Links:

Home Page

Referenced by:

§ ‣ Software Cross Index, § ‣ Software Cross Index, A. L. Van Buren and J. E. Boisvert (2002), A. L. Van Buren and J. E. Boisvert (2004), A. L. Van Buren and J. E. Boisvert (2007).

Encodings:

BibTeX

…