23 Weierstrass Elliptic and Modular FunctionsWeierstrass Elliptic Functions23.3 Differential Equations23.5 Special Lattices
§23.4 Graphics
Contents
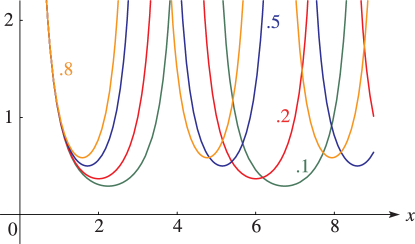
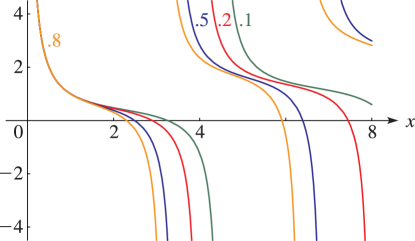
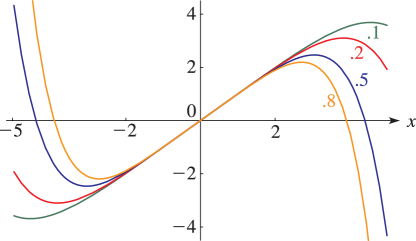
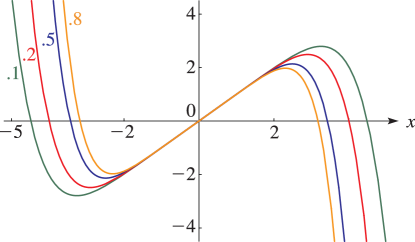
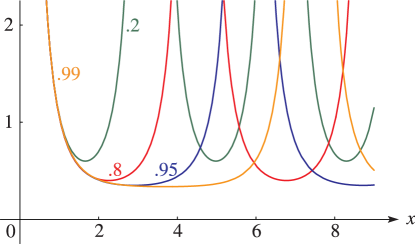
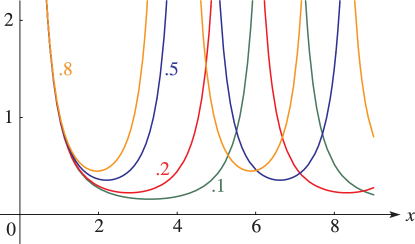
§23.4(i) Real Variables
Line graphs of the Weierstrass functions , , and , illustrating the lemniscatic and equianharmonic cases. (The figures in this subsection may be compared with the figures in §22.3(i).)
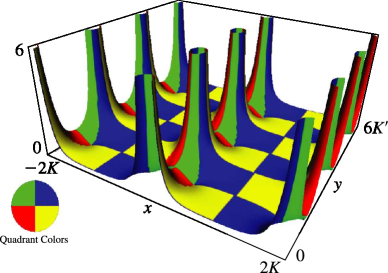
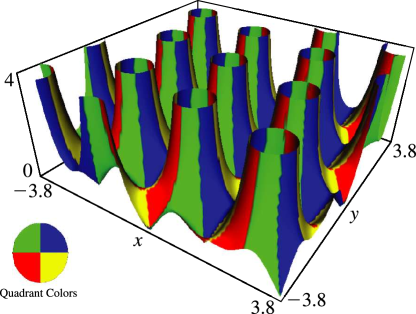
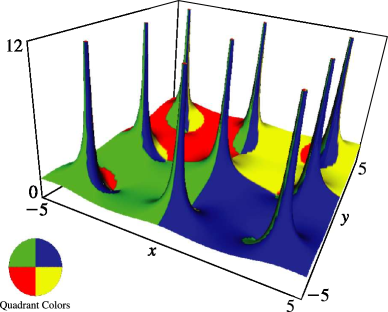
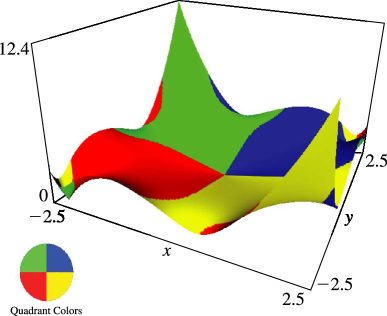
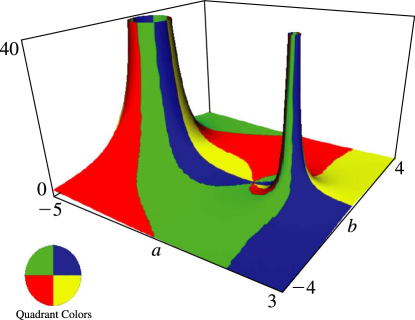
§23.4(ii) Complex Variables
Surfaces for the Weierstrass functions , , and . Height corresponds to the absolute value of the function and color to the phase. See also About Color Map. (The figures in this subsection may be compared with the figures in §22.3(iii).)