principal branches (or values)

SearchAdvancedHelp

(0.003 seconds)

21—30 of 178 matching pages

21: 32.11 Asymptotic Approximations for Real Variables

… ►

32.11.8 $$d^2=-{\pi }^{-1}\ln \left(1-k^2\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\ln z$: principal branch of logarithm function, $k$: real and $d$: constant

Permalink:

http://dlmf.nist.gov/32.11.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §32.11(ii), §32.11 and Ch.32

… ►

32.11.17 $$d^2={\pi }^{-1}\ln \left(1+k^2\right),$$ $\mathrm{sign}\left(k\right)={(-1)}^n$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\ln z$: principal branch of logarithm function, $\mathrm{sign}x$: sign of, $n$: integer, $k$: real and $d$: constant

Permalink:

http://dlmf.nist.gov/32.11.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §32.11(iii), §32.11 and Ch.32

… ►

32.11.20 $$\psi (x)=\frac{2}{3}\sqrt{2}{x}^{3/2}-\frac{3}{2}{\rho }^2\ln x.$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $x$: real, $\rho$: real constant and $\psi (z)$: function

Permalink:

http://dlmf.nist.gov/32.11.E20

Encodings:

pMML, png, TeX

See also:

Annotations for §32.11(iii), §32.11 and Ch.32

… ►

32.11.34 $$\varphi (x)=\frac{1}{3}\sqrt{3}{x}^2-\frac{4}{3}{d}^2\sqrt{3}\ln \left(\sqrt{2}|x|\right),$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $x$: real, $\varphi (z)$: function and $d$: constant

Permalink:

http://dlmf.nist.gov/32.11.E34

Encodings:

pMML, png, TeX

See also:

Annotations for §32.11(v), §32.11 and Ch.32

… ►

32.11.35 $$d^2=-\frac{1}{4}\sqrt{3}{\pi }^{-1}\ln \left(1-{|\mu |}^2\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\ln z$: principal branch of logarithm function, $d$: constant and $\mu$

Permalink:

http://dlmf.nist.gov/32.11.E35

Encodings:

pMML, png, TeX

See also:

Annotations for §32.11(v), §32.11 and Ch.32

…

22: 25.8 Sums

… ►

25.8.4 $$\sum _{k=1}^{\mathrm{\infty }}\frac{{(-1)}^k}{k}(\zeta \left(nk\right)-1)=\ln \left(\prod _{j=0}^{n-1}\mathrm{\Gamma }\left(2-{\mathrm{e}}^{(2j+1)\pi \mathrm{i}/n}\right)\right),$$ $n=2,3,4,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\zeta \left(s\right)$: Riemann zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\ln z$: principal branch of logarithm function, $k$: nonnegative integer and $n$: nonnegative integer

Keywords:

infinite series

Source:

Adamchik and Srivastava (1998, (2.7), p. 135)

Permalink:

http://dlmf.nist.gov/25.8.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §25.8 and Ch.25

… ►

25.8.7 $$\sum _{k=2}^{\mathrm{\infty }}\frac{\zeta \left(k\right)}{k}{z}^k=-\gamma z+\ln \mathrm{\Gamma }\left(1-z\right),$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\gamma$: Euler’s constant, $\zeta \left(s\right)$: Riemann zeta function, $\ln z$: principal branch of logarithm function, $k$: nonnegative integer and $z$: complex variable

Keywords:

infinite series

Proof sketch:

Derivable from (25.8.5) by dividing by $z$ and integrating.

Permalink:

http://dlmf.nist.gov/25.8.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §25.8 and Ch.25

►

25.8.8 $$\sum _{k=1}^{\mathrm{\infty }}\frac{\zeta \left(2k\right)}{k}{z}^{2k}=\ln \left(\frac{\pi z}{\sin \left(\pi z\right)}\right),$$ .

ⓘ

Symbols:

$\zeta \left(s\right)$: Riemann zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\ln z$: principal branch of logarithm function, $\sin z$: sine function, $k$: nonnegative integer and $z$: complex variable

Keywords:

infinite series

Proof sketch:

Derivable from (25.8.6) by dividing by $z$ and integrating.

Permalink:

http://dlmf.nist.gov/25.8.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §25.8 and Ch.25

►

25.8.9 $$\sum _{k=1}^{\mathrm{\infty }}\frac{\zeta \left(2k\right)}{(2k+1)2^{2k}}=\frac{1}{2}-\frac{1}{2}\ln 2.$$

ⓘ

Symbols:

$\zeta \left(s\right)$: Riemann zeta function, $\ln z$: principal branch of logarithm function and $k$: nonnegative integer

Keywords:

infinite series

Source:

Srivastava and Choi (2001, (467), p. 212)

Permalink:

http://dlmf.nist.gov/25.8.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §25.8 and Ch.25

…

23: 6.8 Inequalities

… ►

6.8.1

ⓘ

Symbols:

$\mathrm{e}$: base of natural logarithm, $E_1\left(z\right)$: exponential integral, $\ln z$: principal branch of logarithm function and $x$: real variable

A&S Ref:

5.1.20

Referenced by:

§6.8

Permalink:

http://dlmf.nist.gov/6.8.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §6.8 and Ch.6

…

24: 4.13 Lambert $W$-Function

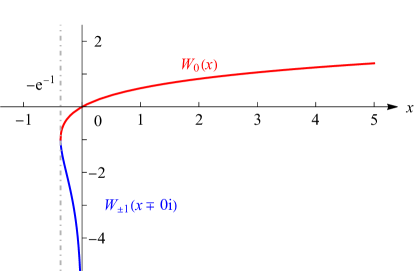
… ►We call the increasing solution for which $W\left(z\right)\ge W\left(-{\mathrm{e}}^{-1}\right)=-1$ the principal branch and denote it by $W_0\left(z\right)$. … ►

►►

Figure 4.13.1: Branches $W_0\left(x\right)$, $W_{\pm 1}\left(x\mp 0\mathrm{i}\right)$ of the Lambert $W$-function. Magnify

… ►

4.13.1_1 $$W_k\left(z\right)={\ln }_k(z)-\ln \left({\ln }_k(z)\right)+o\left(1\right),$$ $\left|z\right|\to \mathrm{\infty }$,

ⓘ

Symbols:

$W\left(z\right)$: Lambert $W$-function, $o\left(x\right)$: order less than, $\ln z$: principal branch of logarithm function, $k$: integer and $z$: complex variable

Notes:

See Corless et al. (1996, §4).

Permalink:

http://dlmf.nist.gov/4.13.E1_1

Encodings:

pMML, png, TeX

Addition (effective with 1.1.7):

This equation was added.

See also:

Annotations for §4.13 and Ch.4

… ►

4.13.1_2 $$\omega \left(z\right)+\ln \left(\omega \left(z\right)\right)=z,$$

ⓘ

Symbols:

$\omega \left(z\right)$: Wright $\omega$-function, $\ln z$: principal branch of logarithm function and $z$: complex variable

Referenced by:

(4.13.3), §4.13, Erratum (V1.1.7) for Expansion

Permalink:

http://dlmf.nist.gov/4.13.E1_2

Encodings:

pMML, png, TeX

Rearrangement (effective with 1.1.7):

This equation, which was originally (4.13.3), was moved here, and the symbol for $\omega$ was originally $U$.

See also:

Annotations for §4.13 and Ch.4

… ►

4.13.16 $$W_0\left(z\right)=\frac{1}{\pi }{\int }_0^{\pi }\ln \left(1+z\frac{\sin t}{t}{\mathrm{e}}^{t\cot t}\right)dt.$$

ⓘ

Symbols:

$W\left(z\right)$: Lambert $W$-function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cot z$: cotangent function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\ln z$: principal branch of logarithm function, $\sin z$: sine function and $z$: complex variable

Notes:

See Mező (2020, formula (3)).

Permalink:

http://dlmf.nist.gov/4.13.E16

Encodings:

pMML, png, TeX

Addition (effective with 1.1.7):

This equation was added.

See also:

Annotations for §4.13 and Ch.4

…

25: 10.31 Power Series

… ►

10.31.1 $$K_n\left(z\right)=\frac{1}{2}{(\frac{1}{2}z)}^{-n}\sum _{k=0}^{n-1}\frac{(n-k-1)!}{k!}{(-\frac{1}{4}{z}^2)}^k+{(-1)}^{n+1}\ln \left(\frac{1}{2}z\right)I_n\left(z\right)+{(-1)}^n\frac{1}{2}{(\frac{1}{2}z)}^n\sum _{k=0}^{\mathrm{\infty }}\left(\psi \left(k+1\right)+\psi \left(n+k+1\right)\right)\frac{{(\frac{1}{4}{z}^2)}^k}{k!(n+k)!},$$

ⓘ

Symbols:

$\psi \left(z\right)$: psi (or digamma) function, $!$: factorial (as in $n!$), $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\ln z$: principal branch of logarithm function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

9.6.11

Referenced by:

§10.30(i), §10.65(ii)

Permalink:

http://dlmf.nist.gov/10.31.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.31 and Ch.10

… ►

10.31.2 $$K_0\left(z\right)=-\left(\ln \left(\frac{1}{2}z\right)+\gamma \right)I_0\left(z\right)+\frac{\frac{1}{4}{z}^2}{{(1!)}^2}+(1+\frac{1}{2})\frac{{(\frac{1}{4}{z}^2)}^2}{{(2!)}^2}+(1+\frac{1}{2}+\frac{1}{3})\frac{{(\frac{1}{4}{z}^2)}^3}{{(3!)}^2}+\mathrm{\cdots }.$$

ⓘ

Symbols:

$\gamma$: Euler’s constant, $!$: factorial (as in $n!$), $I_{\nu }\left(z\right)$: modified Bessel function of the first kind, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\ln z$: principal branch of logarithm function and $z$: complex variable

A&S Ref:

9.6.13

Referenced by:

§10.45

Permalink:

http://dlmf.nist.gov/10.31.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.31 and Ch.10

…

26: 19.27 Asymptotic Approximations and Expansions

… ►

19.27.2 $$R_F(x,y,z)=\frac{1}{2\sqrt{z}}\left(\ln \frac{8z}{a+g}\right)\left(1+O\left(\frac{a}{z}\right)\right),$$ $a/z\to 0$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_F(x,y,z)$: symmetric elliptic integral of first kind, $\ln z$: principal branch of logarithm function, $a$ and $g$

Referenced by:

§19.20(iii), §19.27(ii)

Permalink:

http://dlmf.nist.gov/19.27.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §19.27(ii), §19.27 and Ch.19

… ►

19.27.4 $$R_G(x,y,z)=\frac{\sqrt{z}}{2}\left(1+O\left(\frac{a}{z}\ln \frac{z}{a}\right)\right),$$ $a/z\to 0$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_G(x,y,z)$: symmetric elliptic integral of second kind, $\ln z$: principal branch of logarithm function and $a$

Permalink:

http://dlmf.nist.gov/19.27.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §19.27(iii), §19.27 and Ch.19

… ►

19.27.6 $$R_G(0,y,z)=\frac{\sqrt{z}}{2}+\frac{y}{8\sqrt{z}}\left(\ln \left(\frac{16z}{y}\right)-1\right)\left(1+O\left(\frac{y}{z}\right)\right),$$ $y/z\to 0$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_G(x,y,z)$: symmetric elliptic integral of second kind and $\ln z$: principal branch of logarithm function

Permalink:

http://dlmf.nist.gov/19.27.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §19.27(iii), §19.27 and Ch.19

… ►

19.27.7 $$R_D(x,y,z)=\frac{3}{2z^{3/2}}\left(\ln \left(\frac{8z}{a+g}\right)-2\right)\left(1+O\left(\frac{a}{z}\right)\right),$$ $a/z\to 0$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_D(x,y,z)$: elliptic integral symmetric in only two variables, $\ln z$: principal branch of logarithm function, $a$ and $g$

Referenced by:

§19.20(iv)

Permalink:

http://dlmf.nist.gov/19.27.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §19.27(iv), §19.27 and Ch.19

… ►

19.27.9 $$R_D(x,y,z)=\frac{3}{\sqrt{xz}(\sqrt{y}+\sqrt{z})}\left(1+O\left(\frac{b}{x}\ln \frac{x}{b}\right)\right),$$ $b/x\to 0$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_D(x,y,z)$: elliptic integral symmetric in only two variables, $\ln z$: principal branch of logarithm function and $b$

Permalink:

http://dlmf.nist.gov/19.27.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §19.27(iv), §19.27 and Ch.19

…

27: 4.45 Methods of Computation

… ►

4.45.2 $$\ln x=2^m\ln \left(1+y\right).$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $m$: integer, $x$: real variable and $y$: real variable

Permalink:

http://dlmf.nist.gov/4.45.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.45(i), §4.45(i), §4.45 and Ch.4

… ►

4.45.3 $$\ln x=\ln \xi +m\ln 10.$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, $m$: integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/4.45.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.45(i), §4.45(i), §4.45 and Ch.4

… ►

4.45.15 $$\ln z=\ln |z|+\mathrm{i}\mathrm{ph}z,$$ $-\pi \le \mathrm{ph}z\le \pi$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{i}$: imaginary unit, $\ln z$: principal branch of logarithm function, $\mathrm{ph}$: phase and $z$: complex variable

Permalink:

http://dlmf.nist.gov/4.45.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §4.45(ii), §4.45 and Ch.4

… ►For $x\in [-1/\mathrm{e},\mathrm{\infty })$ the principal branch $\mathrm{Wp}\left(x\right)$ can be computed by solving the defining equation $W{\mathrm{e}}^W=x$ numerically, for example, by Newton’s rule (§3.8(ii)). …

28: 19.12 Asymptotic Approximations

… ►

19.12.1 $$K\left(k\right)=\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\left(\frac{1}{2}\right)}_m}{m!m!}k_{}^{\prime }{}_{}{}^{2m}\left(\ln \left(\frac{1}{k^{\prime }}\right)+d(m)\right),$$ ,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $K\left(k\right)$: Legendre’s complete elliptic integral of the first kind, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $m$: nonnegative integer, $k$: real or complex modulus, $k^{\prime }$: complementary modulus and $d(m)$: function

Referenced by:

§19.12

Permalink:

http://dlmf.nist.gov/19.12.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

►

19.12.2 $$E\left(k\right)=1+\frac{1}{2}\sum _{m=0}^{\mathrm{\infty }}\frac{{\left(\frac{1}{2}\right)}_m{\left(\frac{3}{2}\right)}_m}{{\left(2\right)}_{m}m!}k_{}^{\prime }{}_{}{}^{2m+2}\left(\ln \left(\frac{1}{k^{\prime }}\right)+d(m)-\frac{1}{(2m+1)(2m+2)}\right),$$ ,

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $E\left(k\right)$: Legendre’s complete elliptic integral of the second kind, $!$: factorial (as in $n!$), $\ln z$: principal branch of logarithm function, $m$: nonnegative integer, $k$: real or complex modulus, $k^{\prime }$: complementary modulus and $d(m)$: function

Referenced by:

§19.12

Permalink:

http://dlmf.nist.gov/19.12.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

… ►

19.12.4 $$(1-{\alpha }^2)\mathrm{\Pi }({\alpha }^2,k)=\left(\ln \frac{4}{k^{\prime }}\right)\left(1+O\left(k_{}^{\prime }{}_{}{}^2\right)\right)-{\alpha }^2{R}_C(1,1-{\alpha }^2),$$ ,

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_C(x,y)$: Carlson’s combination of inverse circular and inverse hyperbolic functions, $\mathrm{\Pi }({\alpha }^2,k)$: Legendre’s complete elliptic integral of the third kind, $\ln z$: principal branch of logarithm function, $k$: real or complex modulus, $k^{\prime }$: complementary modulus and ${\alpha }^2$: real or complex parameter

Referenced by:

§19.12

Permalink:

http://dlmf.nist.gov/19.12.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

►

19.12.5 $$(1-{\alpha }^2)\mathrm{\Pi }({\alpha }^2,k)=\left(\ln \left(\frac{4}{k^{\prime }}\right)-R_C(1,1-{\alpha }^{-2})\right)\left(1+O\left(k_{}^{\prime }{}_{}{}^2\right)\right),$$ .

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_C(x,y)$: Carlson’s combination of inverse circular and inverse hyperbolic functions, $\mathrm{\Pi }({\alpha }^2,k)$: Legendre’s complete elliptic integral of the third kind, $\ln z$: principal branch of logarithm function, $k$: real or complex modulus, $k^{\prime }$: complementary modulus and ${\alpha }^2$: real or complex parameter

Referenced by:

§19.12

Permalink:

http://dlmf.nist.gov/19.12.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

… ►

19.12.7 $$R_C(x,y)=\frac{1}{2\sqrt{x}}\left(\left(1+\frac{y}{2x}\right)\ln \left(\frac{4x}{y}\right)-\frac{y}{2x}\right)(1+O\left(y^2/x^2\right)),$$ $y/x\to 0$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $R_C(x,y)$: Carlson’s combination of inverse circular and inverse hyperbolic functions and $\ln z$: principal branch of logarithm function

Referenced by:

§19.12, §19.2(iv)

Permalink:

http://dlmf.nist.gov/19.12.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §19.12 and Ch.19

29: 25.12 Polylogarithms

… ►Other notations and names for ${\mathrm{Li}}_2\left(z\right)$ include $S_2(z)$ (Kölbig et al. (1970)), Spence function $\mathrm{Sp}(z)$ (’t Hooft and Veltman (1979)), and ${\mathrm{L}}_2(z)$ (Maximon (2003)). … ►The principal branch has a cut along the interval $[1,\mathrm{\infty })$ and agrees with (25.12.1) when $|z|\le 1$; see also §4.2(i). The remainder of the equations in this subsection apply to principal branches. … ►

25.12.6 $${\mathrm{Li}}_2\left(x\right)+{\mathrm{Li}}_2\left(1-x\right)=\frac{1}{6}{\pi }^2-(\ln x)\ln \left(1-x\right),$$ .

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{Li}}_2\left(z\right)$: dilogarithm, $\ln z$: principal branch of logarithm function and $x$: real variable

Keywords:

connection formula

Source:

Maximon (2003, (3.3), p. 2808)

Permalink:

http://dlmf.nist.gov/25.12.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §25.12(i), §25.12 and Ch.25

… ►

25.12.9 $$\sum _{n=1}^{\mathrm{\infty }}\frac{\sin \left(n\theta \right)}{n^2}=-{\int }_0^{\theta }\ln \left(2\sin \left(\frac{1}{2}x\right)\right)dx.$$

ⓘ

Symbols:

$dx$: differential of $x$ , $\int$: integral, $\ln z$: principal branch of logarithm function, $\sin z$: sine function, $n$: nonnegative integer, $x$: real variable and $\theta$: phase

Keywords:

definite integral, infinite series

Source:

Maximon (2003, (8.7), (8.8), p. 2813)

A&S Ref:

27.8.6 (integration of first series)

Referenced by:

1st item

Permalink:

http://dlmf.nist.gov/25.12.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §25.12(i), §25.12 and Ch.25

…

30: 4.26 Integrals

… ►

4.26.3 $$\int \tan xdx=-\ln \left(\cos x\right),$$ .

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\int$: integral, $\ln z$: principal branch of logarithm function, $\tan z$: tangent function and $x$: real variable

A&S Ref:

4.3.115

Permalink:

http://dlmf.nist.gov/4.26.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.26(ii), §4.26 and Ch.4

►

4.26.4 $$\int \csc xdx=\ln \left(\tan \frac{1}{2}x\right),$$ .

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\csc z$: cosecant function, $dx$: differential of $x$ , $\int$: integral, $\ln z$: principal branch of logarithm function, $\tan z$: tangent function and $x$: real variable

A&S Ref:

4.3.116

Permalink:

http://dlmf.nist.gov/4.26.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.26(ii), §4.26 and Ch.4

… ►

4.26.6 $$\int \cot xdx=\ln \left(\sin x\right),$$ .

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cot z$: cotangent function, $dx$: differential of $x$ , $\int$: integral, $\ln z$: principal branch of logarithm function, $\sin z$: sine function and $x$: real variable

A&S Ref:

4.3.118

Permalink:

http://dlmf.nist.gov/4.26.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.26(ii), §4.26 and Ch.4

… ►

4.26.16 $$\int \arctan xdx=x\arctan x-\frac{1}{2}\ln \left(1+x^2\right),$$ ,

ⓘ

Symbols:

$dx$: differential of $x$ , $\int$: integral, $\arctan z$: arctangent function, $\ln z$: principal branch of logarithm function and $x$: real variable

A&S Ref:

4.4.60 (modified)

Permalink:

http://dlmf.nist.gov/4.26.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §4.26(iv), §4.26 and Ch.4

►

4.26.17 $$\int \mathrm{arccsc}xdx=x\mathrm{arccsc}x+\ln \left(x+{(x^2-1)}^{1/2}\right),$$ ,

ⓘ

Symbols:

$dx$: differential of $x$ , $\int$: integral, $\mathrm{arccsc}z$: arccosecant function, $\ln z$: principal branch of logarithm function and $x$: real variable

A&S Ref:

4.4.61 (is stated differently.)

Permalink:

http://dlmf.nist.gov/4.26.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §4.26(iv), §4.26 and Ch.4

…