Racah%20polynomials
(0.001 seconds)
21—30 of 316 matching pages
21: 6.20 Approximations
Cody and Thacher (1968) provides minimax rational approximations for , with accuracies up to 20S.
Cody and Thacher (1969) provides minimax rational approximations for , with accuracies up to 20S.
MacLeod (1996b) provides rational approximations for the sine and cosine integrals and for the auxiliary functions and , with accuracies up to 20S.
22: 24.18 Physical Applications
§24.18 Physical Applications
►Bernoulli polynomials appear in statistical physics (Ordóñez and Driebe (1996)), in discussions of Casimir forces (Li et al. (1991)), and in a study of quark-gluon plasma (Meisinger et al. (2002)). ►Euler polynomials also appear in statistical physics as well as in semi-classical approximations to quantum probability distributions (Ballentine and McRae (1998)).23: 7.24 Approximations
Hastings (1955) gives several minimax polynomial and rational approximations for , and the auxiliary functions and .
Cody (1969) provides minimax rational approximations for and . The maximum relative precision is about 20S.
Cody et al. (1970) gives minimax rational approximations to Dawson’s integral (maximum relative precision 20S–22S).
24: 32.8 Rational Solutions
25: 25.20 Approximations
Cody et al. (1971) gives rational approximations for in the form of quotients of polynomials or quotients of Chebyshev series. The ranges covered are , , , . Precision is varied, with a maximum of 20S.
26: Bibliography K
27: 24.3 Graphs
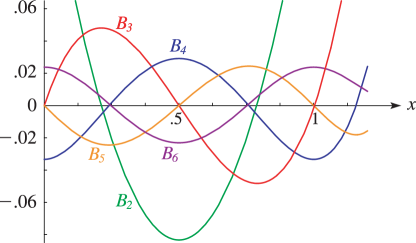 ►
►
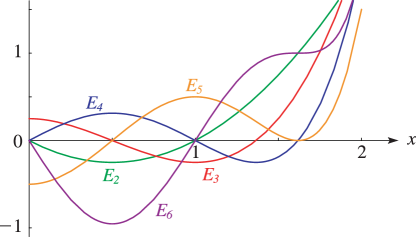 ►
►
28: 18.4 Graphics
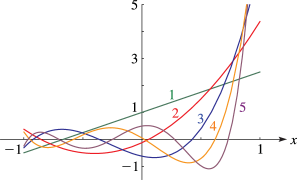 ►
►
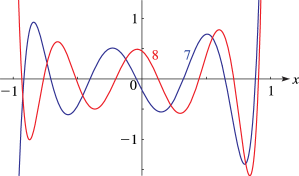 ►
►
 ►
►
 ►
►
 ►
►
