Legendre functions on the cut

SearchAdvancedHelp

(0.003 seconds)

1—10 of 19 matching pages

1: 14.1 Special Notation

… ►The main functions treated in this chapter are the Legendre functions ${𝖯}_{\nu }\left(x\right)$, ${𝖰}_{\nu }\left(x\right)$, $P_{\nu }\left(z\right)$, $Q_{\nu }\left(z\right)$; Ferrers functions ${𝖯}_{\nu }^{\mu }\left(x\right)$, ${𝖰}_{\nu }^{\mu }\left(x\right)$ (also known as the Legendre functions on the cut); associated Legendre functions $P_{\nu }^{\mu }\left(z\right)$, $Q_{\nu }^{\mu }\left(z\right)$, ${𝑸}_{\nu }^{\mu }\left(z\right)$; conical functions ${𝖯}_{-\frac{1}{2}+\mathrm{i}\tau }^{\mu }\left(x\right)$, ${𝖰}_{-\frac{1}{2}+\mathrm{i}\tau }^{\mu }\left(x\right)$, ${\widehat{𝖰}}_{-\frac{1}{2}+\mathrm{i}\tau }^{\mu }\left(x\right)$, $P_{-\frac{1}{2}+\mathrm{i}\tau }^{\mu }\left(x\right)$, $Q_{-\frac{1}{2}+\mathrm{i}\tau }^{\mu }\left(x\right)$ (also known as Mehler functions). …

2: 14.23 Values on the Cut

§14.23 Values on the Cut

…

3: Bibliography O

… ►

Associated Legendre functions on the cut. J. Comput. Phys. 51 (3), pp. 502–518.

ⓘ

Notes:

Includes single, double precision Fortran code.

External Links:

GAMS (module DXNRMP; package SLATEC), ISSN 0021-9991, Document, MathReview (G. P. Bhattacharjee), ZentralBlatt

Referenced by:

§14.32, 7th item.

Encodings:

BibTeX

…

4: Mathematical Introduction

… ►Other examples are: (a) the notation for the Ferrers functions—also known as associated Legendre functions on the cut—for which existing notations can easily be confused with those for other associated Legendre functions (§14.1); (b) the spherical Bessel functions for which existing notations are unsymmetric and inelegant (§§10.47(i) and 10.47(ii)); and (c) elliptic integrals for which both Legendre’s forms and the more recent symmetric forms are treated fully (Chapter 19). …

5: Bibliography S

… ►

Evaluation of associated Legendre functions off the cut and parabolic cylinder functions. Electron. Trans. Numer. Anal. 9, pp. 137–146.

ⓘ

Notes:

Orthogonal polynomials: numerical and symbolic algorithms (Leganés, 1998)

External Links:

ISSN 1068-9613, FullText, MathReview (Adam Marlewski), ZentralBlatt

Referenced by:

§14.30(i), 3rd item.

Encodings:

BibTeX

…

6: 14.27 Zeros

§14.27 Zeros

► $P_{\nu }^{\mu }\left(x\pm \mathrm{i}0\right)$ (either side of the cut) has exactly one zero in the interval $(-\mathrm{\infty },-1)$ if either of the following sets of conditions holds: …For all other values of the parameters $P_{\nu }^{\mu }\left(x\pm \mathrm{i}0\right)$ has no zeros in the interval $(-\mathrm{\infty },-1)$. ►For complex zeros of $P_{\nu }^{\mu }\left(z\right)$ see Hobson (1931, §§233, 234, and 238).

7: 14.22 Graphics

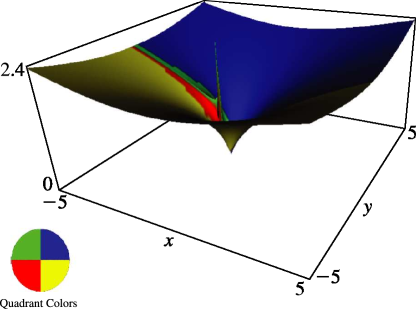
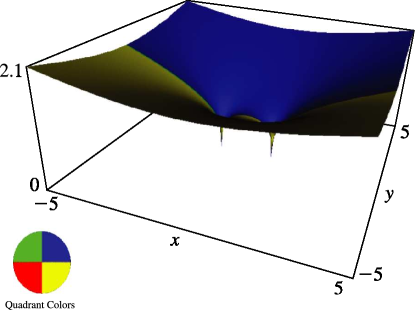
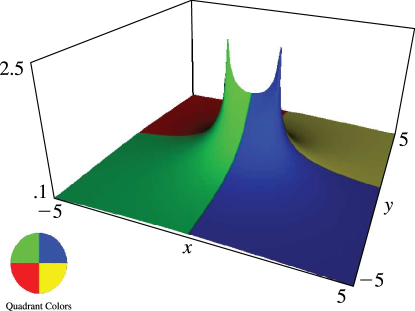
§14.22 Graphics

►In the graphics shown in this section, height corresponds to the absolute value of the function and color to the phase. … ►

►

►

Figure 14.22.1: $P_{1/2}^0\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. There is a cut along the real axis from $-\mathrm{\infty }$ to $-1$. Magnify 3D Help

►

►

►

Figure 14.22.2: $P_{1/2}^{-1/2}\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. There is a cut along the real axis from $-\mathrm{\infty }$ to $1$. Magnify 3D Help

… ►

►

►

Figure 14.22.4: ${𝑸}_0^0\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. … Magnify 3D Help

8: 30.5 Functions of the Second Kind

… ►

30.5.3 $${\mathrm{𝖰𝗌}}_n^m(x,0)={𝖰}_n^m\left(x\right);$$

ⓘ

Symbols:

: Ferrers function of the second kind, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer and $n\ge m$: integer degree

Permalink:

http://dlmf.nist.gov/30.5.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §30.5 and Ch.30

…

9: 30.4 Functions of the First Kind

… ►If $\gamma =0$, ${\mathrm{𝖯𝗌}}_n^m(x,0)$ reduces to the Ferrers function ${𝖯}_n^m\left(x\right)$: ►

30.4.2 $${\mathrm{𝖯𝗌}}_n^m(x,0)={𝖯}_n^m\left(x\right);$$

ⓘ

Symbols:

: Ferrers function of the first kind, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, $x$: real variable, $m$: nonnegative integer and $n\ge m$: integer degree

Referenced by:

§30.4(iv)

Permalink:

http://dlmf.nist.gov/30.4.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §30.4(i), §30.4 and Ch.30

…

10: 30.8 Expansions in Series of Ferrers Functions

… ►

30.8.1 $${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)=\sum _{k=-R}^{\mathrm{\infty }}{(-1)}^k{a}_{n,k}^m({\gamma }^2){𝖯}_{n+2k}^m\left(x\right),$$

ⓘ

Symbols:

: Ferrers function of the first kind, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $R=\lfloor (n-m)/2\rfloor$: limit and $a_{n,k}^m({\gamma }^2)$: coefficients

A&S Ref:

21.7.1 (in different form)

Referenced by:

§30.16(ii), §30.16(ii)

Permalink:

http://dlmf.nist.gov/30.8.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §30.8(i), §30.8 and Ch.30

… ►

30.8.2 $$a_{n,k}^m({\gamma }^2)={(-1)}^k\left(n+2k+\frac{1}{2}\right)\frac{(n-m+2k)!}{(n+m+2k)!}{\int }_{-1}^1{\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2){𝖯}_{n+2k}^m\left(x\right)dx.$$

ⓘ

Defines:

$a_{n,k}^m({\gamma }^2)$: coefficients (locally)

Symbols:

: Ferrers function of the first kind, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Referenced by:

§30.11(i)

Permalink:

http://dlmf.nist.gov/30.8.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §30.8(i), §30.8 and Ch.30

… ►

30.8.9 $${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)=\sum _{k=-\mathrm{\infty }}^{-N-1}{(-1)}^{k}a_{}^{\prime }{}_{n,k}{}^m({\gamma }^2){𝖯}_{n+2k}^m\left(x\right)+\sum _{k=-N}^{\mathrm{\infty }}{(-1)}^k{a}_{n,k}^m({\gamma }^2){𝖰}_{n+2k}^m\left(x\right),$$

ⓘ

Symbols:

: Ferrers function of the first kind, : Ferrers function of the second kind, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $a_{n,k}^m({\gamma }^2)$: coefficients and $N$: upper limit

A&S Ref:

21.7.21 (in different form)

Permalink:

http://dlmf.nist.gov/30.8.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §30.8(ii), §30.8 and Ch.30

…