Bernoulli polynomials

SearchAdvancedHelp

(0.002 seconds)

1—10 of 51 matching pages

1: 24.1 Special Notation

… ►

Bernoulli Numbers and Polynomials

►The origin of the notation $B_n$, $B_n\left(x\right)$, is not clear. …

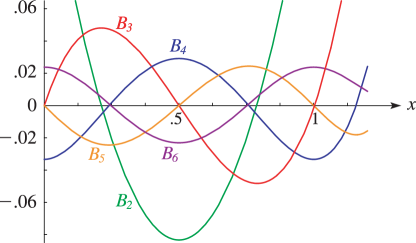
2: 24.3 Graphs

… ►

►►

Figure 24.3.1: Bernoulli polynomials $B_n\left(x\right)$, $n=2,3,\mathrm{\dots },6$. Magnify

…

3: 24.16 Generalizations

… ►For $\mathrm{\ell }=0,1,2,\mathrm{\dots }$, Bernoulli and Euler polynomials of order $\mathrm{\ell }$ are defined respectively by … ►

$B_n^{(\mathrm{\ell })}=B_n^{(\mathrm{\ell })}\left(0\right),$

… ►For extensions of $B_n^{(\mathrm{\ell })}\left(x\right)$ to complex values of $x$, $n$, and $\mathrm{\ell }$, and also for uniform asymptotic expansions for large $x$ and large $n$, see Temme (1995b) and López and Temme (1999b, 2010b). … ►

24.16.6 $$n!b_n=-\frac{1}{n-1}{B}_n^{(n-1)},$$ $n=2,3,\mathrm{\dots }$.

ⓘ

Symbols:

$!$: factorial (as in $n!$), $B_n^{(\mathrm{\ell })}\left(x\right)$: generalized Bernoulli polynomials, $n$: integer and $b_n$

Referenced by:

§24.16(i)

Permalink:

http://dlmf.nist.gov/24.16.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §24.16(i), §24.16(i), §24.16 and Ch.24

… ► $B_n^{(x)}$ is a polynomial in $x$ of degree $n$. …

4: 24.4 Basic Properties

… ►

24.4.1 $$B_n\left(x+1\right)-B_n\left(x\right)=n{x}^{n-1},$$

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $n$: integer and $x$: real or complex

A&S Ref:

23.1.6

Referenced by:

(13.8.16), §24.13(i)

Permalink:

http://dlmf.nist.gov/24.4.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §24.4(i), §24.4 and Ch.24

… ►

24.4.3 $$B_n\left(1-x\right)={(-1)}^n{B}_n\left(x\right),$$

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $n$: integer and $x$: real or complex

A&S Ref:

23.1.8

Permalink:

http://dlmf.nist.gov/24.4.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §24.4(ii), §24.4 and Ch.24

… ►

24.4.5 $${(-1)}^n{B}_n\left(-x\right)=B_n\left(x\right)+n{x}^{n-1},$$

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $n$: integer and $x$: real or complex

A&S Ref:

23.1.9

Permalink:

http://dlmf.nist.gov/24.4.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §24.4(ii), §24.4 and Ch.24

… ►

24.4.21 $$B_n\left(x\right)=2^{n-1}\left(B_n\left(\frac{1}{2}x\right)+B_n\left(\frac{1}{2}x+\frac{1}{2}\right)\right),$$

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $n$: integer and $x$: real or complex

Permalink:

http://dlmf.nist.gov/24.4.E21

Encodings:

pMML, png, TeX

See also:

Annotations for §24.4(v), §24.4(v), §24.4 and Ch.24

… ►

§24.4(vii) Derivatives

…

5: 24.18 Physical Applications

§24.18 Physical Applications

►Bernoulli polynomials appear in statistical physics (Ordóñez and Driebe (1996)), in discussions of Casimir forces (Li et al. (1991)), and in a study of quark-gluon plasma (Meisinger et al. (2002)). …

6: 25.1 Special Notation

… ► ►►►►

$k,m,n$	nonnegative integers.
…
$B_n,B_n\left(x\right)$	Bernoulli number and polynomial (§24.2(i)).
${\tilde{B}}_n\left(x\right)$	periodic Bernoulli function $B_n\left(x-\lfloor x\rfloor \right)$.
…

…

7: 24.13 Integrals

… ►

§24.13(i) Bernoulli Polynomials

►

24.13.1 $$\int B_n\left(t\right)dt=\frac{B_{n+1}\left(t\right)}{n+1}+\text{const.},$$

ⓘ

Symbols:

$B_n\left(x\right)$: Bernoulli polynomials, $dx$: differential of $x$ , $\int$: integral, $n$: integer and $t$: real or complex

A&S Ref:

23.1.11

Referenced by:

§24.13(i)

Permalink:

http://dlmf.nist.gov/24.13.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §24.13(i), §24.13 and Ch.24

… ►

24.13.6 $${\int }_0^1{B}_n\left(t\right)B_m\left(t\right)dt=\frac{{(-1)}^{n-1}m!n!}{(m+n)!}{B}_{m+n}.$$

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $B_n\left(x\right)$: Bernoulli polynomials, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, $m$: integer, $n$: integer and $t$: real or complex

A&S Ref:

23.1.12

Referenced by:

§24.13(i)

Permalink:

http://dlmf.nist.gov/24.13.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §24.13(i), §24.13 and Ch.24

►For integrals of the form ${\int }_0^x{B}_n\left(t\right)B_m\left(t\right)dt$ and ${\int }_0^x{B}_n\left(t\right)B_m\left(t\right)B_k\left(t\right)dt$ see Agoh and Dilcher (2011). … ►

§24.13(iii) Compendia

…

8: 24.21 Software

… ►

§24.21(ii) $B_n$, $B_n\left(x\right)$, $E_n$, and $E_n\left(x\right)$

…

9: 24.2 Definitions and Generating Functions

… ►

24.2.4 $$B_n=B_n\left(0\right),$$

ⓘ

Symbols:

$B_n$: Bernoulli numbers, $B_n\left(x\right)$: Bernoulli polynomials and $n$: integer

A&S Ref:

23.1.2

Referenced by:

(25.11.7)

Permalink:

http://dlmf.nist.gov/24.2.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §24.2(i), §24.2 and Ch.24

… ►

${\tilde{B}}_n\left(x\right)=B_n\left(x\right)$ ,

… ►

${\tilde{B}}_n\left(x+1\right)={\tilde{B}}_n\left(x\right),$

… ►

Table 24.2.2: Bernoulli and Euler polynomials.

► ►►

$n$	$B_n\left(x\right)$	$E_n\left(x\right)$
…

►

…

10: 24.17 Mathematical Applications

§24.17 Mathematical Applications

… ►

24.17.5

ⓘ

Symbols:

$B_n$: Bernoulli numbers, ${\tilde{B}}_n\left(x\right)$: periodic Bernoulli functions, $n$: integer, $x$: real or complex and $M_n(x)$: function

Permalink:

http://dlmf.nist.gov/24.17.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §24.17(ii), §24.17(ii), §24.17 and Ch.24

… ►

24.17.8 $$F(x)={\tilde{B}}_n\left(x\right)-2^{-n}{B}_n$$

ⓘ

Symbols:

$B_n$: Bernoulli numbers, ${\tilde{B}}_n\left(x\right)$: periodic Bernoulli functions, $n$: integer and $x$: real or complex

Permalink:

http://dlmf.nist.gov/24.17.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §24.17(ii), §24.17(ii), §24.17 and Ch.24

… ►

§24.17(iii) Number Theory

… ►