Bernoulli
(0.001 seconds)
1—10 of 66 matching pages
1: 24.1 Special Notation
2: 24.18 Physical Applications
§24.18 Physical Applications
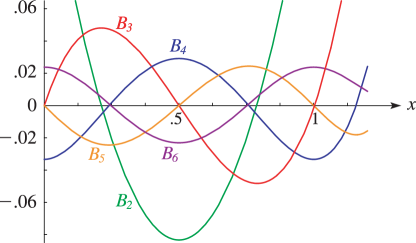
►Bernoulli polynomials appear in statistical physics (Ordóñez and Driebe (1996)), in discussions of Casimir forces (Li et al. (1991)), and in a study of quark-gluon plasma (Meisinger et al. (2002)). …3: 24.3 Graphs
4: 24.4 Basic Properties
…
►
§24.4(ii) Symmetry
… ►§24.4(v) Multiplication Formulas
►Raabe’s Theorem
… ►§24.4(vii) Derivatives
… ►§24.4(ix) Relations to Other Functions
…5: 24.16 Generalizations
§24.16 Generalizations
… ►Bernoulli Numbers of the Second Kind
… ►Degenerate Bernoulli Numbers
… ►§24.16(ii) Character Analogs
… ►§24.16(iii) Other Generalizations
…6: 24.19 Methods of Computation
…
►
•
…
§24.19(i) Bernoulli and Euler Numbers and Polynomials
… ►For algorithms for computing , , , and see Spanier and Oldham (1987, pp. 37, 41, 171, and 179–180). ►§24.19(ii) Values of Modulo
… ►We list here three methods, arranged in increasing order of efficiency. ►Tanner and Wagstaff (1987) derives a congruence for Bernoulli numbers in terms of sums of powers. See also §24.10(iii).
7: 24.14 Sums
§24.14 Sums
►§24.14(i) Quadratic Recurrence Relations
… ►
24.14.2
…
►
§24.14(ii) Higher-Order Recurrence Relations
… ►For other sums involving Bernoulli and Euler numbers and polynomials see Hansen (1975, pp. 331–347) and Prudnikov et al. (1990, pp. 383–386).8: 24.13 Integrals
…
►
§24.13(i) Bernoulli Polynomials
… ►
24.13.4
…
►
24.13.6
►For integrals of the form and see Agoh and Dilcher (2011).
…
►