zonal spherical harmonics

SearchAdvancedHelp

(0.001 seconds)

11—20 of 110 matching pages

11: 35.9 Applications

… ►In chemistry, Wei and Eichinger (1993) expresses the probability density functions of macromolecules in terms of generalized hypergeometric functions of matrix argument, and develop asymptotic approximations for these density functions. ►In the nascent area of applications of zonal polynomials to the limiting probability distributions of symmetric random matrices, one of the most comprehensive accounts is Rains (1998).

12: 29.18 Mathematical Applications

… ►(29.18.5) is the differential equation of spherical Bessel functions (§10.47(i)), and (29.18.6), (29.18.7) agree with the Lamé equation (29.2.1). … ►

§29.18(iii) Spherical and Ellipsoidal Harmonics

…

13: 10.73 Physical Applications

… ► … ►

§10.73(ii) Spherical Bessel Functions

►The functions ${𝗃}_n\left(x\right)$, ${𝗒}_n\left(x\right)$, ${𝗁}_n^{(1)}\left(x\right)$, and ${𝗁}_n^{(2)}\left(x\right)$ arise in the solution (again by separation of variables) of the Helmholtz equation in spherical coordinates $\rho ,\theta ,\varphi$ (§1.5(ii)): …With the spherical harmonic $Y_{\mathrm{\ell },m}\left(\theta ,\varphi \right)$ defined as in §14.30(i), the solutions are of the form $f=g_{\mathrm{\ell }}(k\rho )Y_{\mathrm{\ell },m}\left(\theta ,\varphi \right)$ with $g_{\mathrm{\ell }}={𝗃}_{\mathrm{\ell }}$, ${𝗒}_{\mathrm{\ell }}$, ${𝗁}_{\mathrm{\ell }}^{(1)}$, or ${𝗁}_{\mathrm{\ell }}^{(2)}$, depending on the boundary conditions. Accordingly, the spherical Bessel functions appear in all problems in three dimensions with spherical symmetry involving the scattering of electromagnetic radiation. …

14: 1.17 Integral and Series Representations of the Dirac Delta

… ►

Bessel Functions and Spherical Bessel Functions (§§10.2(ii), 10.47(ii))

… ►

1.17.14 $$\delta \left(x-a\right)=\frac{2xa}{\pi }{\int }_0^{\mathrm{\infty }}{t}^2{𝗃}_{\mathrm{\ell }}\left(xt\right){𝗃}_{\mathrm{\ell }}\left(at\right)dt,$$ $x>0$, $a>0$.

ⓘ

Symbols:

$\delta \left(x-a\right)$: Dirac delta (or Dirac delta function), $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral and ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind

Referenced by:

§1.17(ii), §1.18(vi)

Permalink:

http://dlmf.nist.gov/1.17.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §1.17(ii), §1.17(ii), §1.17 and Ch.1

… ►

1.17.22 $$\delta \left(x-a\right)=\sum _{k=0}^{\mathrm{\infty }}(k+\frac{1}{2})P_k\left(x\right)P_k\left(a\right).$$

ⓘ

Symbols:

$\delta \left(x-a\right)$: Dirac delta (or Dirac delta function), $P_n\left(x\right)$: Legendre polynomial and $k$: integer

Referenced by:

§1.17(iii), §1.17(iv), §14.18(iii)

Permalink:

http://dlmf.nist.gov/1.17.E22

Encodings:

pMML, png, TeX

See also:

Annotations for §1.17(iii), §1.17(iii), §1.17 and Ch.1

… ►

Spherical Harmonics (§14.30)

►

1.17.25 $$\delta \left(\cos {\theta }_1-\cos {\theta }_2\right)\delta \left({\varphi }_1-{\varphi }_2\right)=\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{Y}_{\mathrm{\ell },m}({\theta }_1,{\varphi }_1)\overline{Y_{\mathrm{\ell },m}({\theta }_2,{\varphi }_2)}.$$

ⓘ

Symbols:

$\delta \left(x-a\right)$: Dirac delta (or Dirac delta function), $\overline{z}$: complex conjugate, $\cos z$: cosine function, $Y_{l,m}(\theta ,\varphi )$: spherical harmonic and $m$: nonnegative integer

Referenced by:

§1.17(iii)

Permalink:

http://dlmf.nist.gov/1.17.E25

Encodings:

pMML, png, TeX

Notational Change (effective with 1.0.19):

As a notational clarification, the second sphericalharmonic in the sum over $\mathrm{\ell }$ has been explicity marked up as a complex conjugate.

See also:

Annotations for §1.17(iii), §1.17(iii), §1.17 and Ch.1

…

15: 10.55 Continued Fractions

§10.55 Continued Fractions

►For continued fractions for ${𝗃}_{n+1}\left(z\right)/{𝗃}_n\left(z\right)$ and ${𝗂}_{n+1}^{(1)}\left(z\right)/{𝗂}_n^{(1)}\left(z\right)$ see Cuyt et al. (2008, pp. 350, 353, 362, 363, 367–369).

16: Bibliography L

… ►

Exact operator solution of the Calogero-Sutherland model. Comm. Math. Phys. 178 (2), pp. 425–452.

ⓘ

Notes:

For a Maple implementation of the algorithm given in this paper for Jack and zonal polynomials see Zeilberger (website).

External Links:

ISSN 0010-3616, Link, MathReview (Kazuhiro Hikami), ZentralBlatt

Referenced by:

§35.12.

Encodings:

BibTeX

… ►

Numerical evaluation of integrals containing a spherical Bessel function by product integration. J. Math. Phys. 22 (7), pp. 1399–1413.

ⓘ

External Links:

ISSN 0022-2488, Document, MathReview (C. W. Clenshaw), ZentralBlatt

Referenced by:

§10.74(vii).

Encodings:

BibTeX

… ►

Optimal cylindrical and spherical Bessel transforms satisfying bound state boundary conditions. Comput. Phys. Comm. 99 (2-3), pp. 297–306.

ⓘ

Notes:

Single-precision Fortran, maximum accuracy 8S.

External Links:

ISSN 0010-4655, Document, Code, ZentralBlatt

Referenced by:

4th item.

Encodings:

BibTeX

… ►

Computations of spheroidal harmonics with complex arguments: A review with an algorithm. Phys. Rev. E 58 (5), pp. 6792–6806.

ⓘ

Notes:

Mathematica package for eigenvalues and solutions of the spheroidal wave equations

External Links:

Code(SpheroidF), Document

Referenced by:

2nd item, 3rd item.

Encodings:

BibTeX

…

17: 10.48 Graphs

§10.48 Graphs

… ►

►►

Figure 10.48.5: ${𝗂}_0^{(1)}\left(x\right)$, ${𝗂}_0^{(2)}\left(x\right)$, ${𝗄}_0\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.6: ${𝗂}_1^{(1)}\left(x\right),{𝗂}_1^{(2)}\left(x\right),{𝗄}_1\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.7: ${𝗂}_5^{(1)}\left(x\right)$, ${𝗂}_5^{(2)}\left(x\right)$, ${𝗄}_5\left(x\right)$, $0\le x\le 8$. Magnify

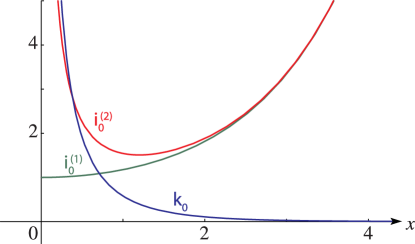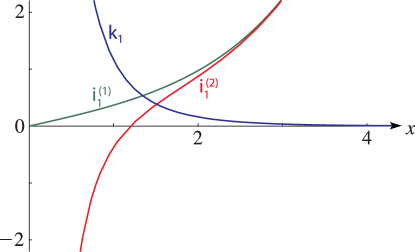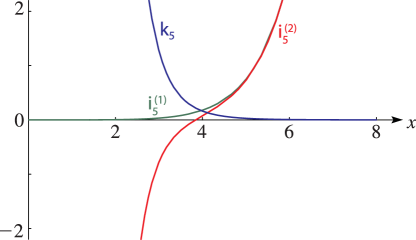18: Bibliography Z

… ►

Doron Zeilberger’s Maple Packages and Programs Department of Mathematics, Rutgers University, New Jersey.

ⓘ

Notes:

Includes hypergeometric and $q$-hypergeometric summation, solution of difference equations (for example, by Petkovšek’s algorithm), combinatorial algorithms, and (package LUC) evaluation of zonal polynomials.

External Links:

Home Page

Referenced by:

§ ‣ Software Cross Index, § ‣ Software Cross Index, L. Lapointe and L. Vinet (1996).

Encodings:

BibTeX

… ►

Tables and formulae for the spherical functions $P_{-1/2+i\tau }^m(z)$ . Translated by E. L. Albasiny, Pergamon Press, Oxford.

ⓘ

Notes:

Translation of Žurina and Karmazina, Tablitsy i formuly dlya sfericheskikh funktsii $P_{-1/2+i\tau }^m(z)$ , Vyčisl. Centr Akad Nauk SSSR, Moscow. 1962

External Links:

MathReview, ZentralBlatt

Referenced by:

§14.20(vii).

Encodings:

BibTeX

…

19: 10.52 Limiting Forms

§10.52 Limiting Forms

… ►

10.52.1 $${𝗃}_n\left(z\right),{𝗂}_n^{(1)}\left(z\right)\sim z^n/(2n+1)!!,$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $!!$: double factorial, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.4

Permalink:

http://dlmf.nist.gov/10.52.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

►

10.52.2 $$-{𝗒}_n\left(z\right),\mathrm{i}{𝗁}_n^{(1)}\left(z\right),-\mathrm{i}{𝗁}_n^{(2)}\left(z\right),{(-1)}^n{𝗂}_n^{(2)}\left(z\right),(2/\pi ){𝗄}_n\left(z\right)\sim (2n-1)!!/z^{n+1}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!!$: double factorial, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, ${𝗁}_n^{(1)}\left(z\right)$: spherical Bessel function of the third kind, ${𝗁}_n^{(2)}\left(z\right)$: spherical Bessel function of the third kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.5

Permalink:

http://dlmf.nist.gov/10.52.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

… ►

${𝗁}_n^{(1)}\left(z\right)\sim {\mathrm{i}}^{-n-1}{z}^{-1}{\mathrm{e}}^{\mathrm{i}z},$

… ►

10.52.5 $${𝗂}_n^{(1)}\left(z\right)\sim {𝗂}_n^{(2)}\left(z\right)\sim \frac{1}{2}{z}^{-1}{\mathrm{e}}^z,$$ ,

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{ph}$: phase, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $z$: complex variable and $\delta$: small positive constant

Permalink:

http://dlmf.nist.gov/10.52.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

…

20: 10.50 Wronskians and Cross-Products

§10.50 Wronskians and Cross-Products

… ►

$$𝒲\left\{{𝗁}_n^{(1)}\left(z\right),{𝗁}_n^{(2)}\left(z\right)\right\}=-2\mathrm{i}{z}^{-2}.$$

►

$$𝒲\left\{{𝗂}_n^{(1)}\left(z\right),{𝗂}_n^{(2)}\left(z\right)\right\}={(-1)}^{n+1}{z}^{-2},$$

►

$$𝒲\left\{{𝗂}_n^{(1)}\left(z\right),{𝗄}_n\left(z\right)\right\}=𝒲\left\{{𝗂}_n^{(2)}\left(z\right),{𝗄}_n\left(z\right)\right\}=-\frac{1}{2}\pi z^{-2}.$$

… ►Results corresponding to (10.50.3) and (10.50.4) for ${𝗂}_n^{(1)}\left(z\right)$ and ${𝗂}_n^{(2)}\left(z\right)$ are obtainable via (10.47.12).