hyperbolic umbilic canonical integral

SearchAdvancedHelp

(0.005 seconds)

1—10 of 14 matching pages

1: 36.2 Catastrophes and Canonical Integrals

… ►

Canonical Integrals

… ►

${\mathrm{\Psi }}^{(\mathrm{H})}\left(\mathrm{𝟎}\right)=\frac{1}{3}{\mathrm{\Gamma }}^2\left(\frac{1}{3}\right)=2.39224.$

… ►

36.2.21 $${\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)=\frac{4{\pi }^2}{3^{2/3}}\mathrm{Ai}\left(\frac{x}{3^{1/3}}\right)\mathrm{Ai}\left(\frac{y}{3^{1/3}}\right).$$

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\pi$: the ratio of the circumference of a circle to its diameter, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $y$: real parameter and $x$: real parameter

Referenced by:

§36.2(ii)

Permalink:

http://dlmf.nist.gov/36.2.E21

Encodings:

pMML, png, TeX

See also:

Annotations for §36.2(ii), §36.2 and Ch.36

… ►

36.2.27 $${\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,z\right)={\mathrm{\Psi }}^{(\mathrm{H})}\left(y,x,z\right).$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.2.E27

Encodings:

pMML, png, TeX

See also:

Annotations for §36.2(iii), §36.2 and Ch.36

… ►

36.2.29 $${\mathrm{\Psi }}^{(\mathrm{H})}\left(0,0,z\right)=\overline{{\mathrm{\Psi }}^{(\mathrm{H})}\left(0,0,-z\right)}=\frac{2^{1/3}}{\sqrt{3}}\exp \left(\frac{1}{27}\mathrm{i}{z}^3\right){\mathrm{\Psi }}^{(\mathrm{E})}\left(0,0,-\frac{z}{2^{2/3}}\right),$$ .

ⓘ

Symbols:

$\overline{z}$: complex conjugate, ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, $\exp z$: exponential function, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit and $z$: real parameter

Referenced by:

Erratum (V1.0.5) for Chapters 8, 20, 36

Permalink:

http://dlmf.nist.gov/36.2.E29

Encodings:

pMML, png, TeX

Addition (effective with 1.0.5):

This equation has been added. For the proof see Berry and Howls (2010).

See also:

Annotations for §36.2(iv), §36.2 and Ch.36

2: 36.3 Visualizations of Canonical Integrals

… ►

…

Figure 36.3.9: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)|$. …

… ►

…

Figure 36.3.18: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)$. …

►

…

Figure 36.3.19: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,1\right)$. …

►

…

Figure 36.3.20: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,2\right)$. …

►

…

Figure 36.3.21: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,3\right)$. …

3: 36.10 Differential Equations

… ►In terms of the normal forms (36.2.2) and (36.2.3), the ${\mathrm{\Psi }}^{(\mathrm{U})}\left(𝐱\right)$ satisfy the following operator equations … ►

36.10.14 $$3\left(\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial x}^2}-\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial y}^2}\right)+2\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{E})}}{\partial x}-x{\mathrm{\Psi }}^{(\mathrm{E})}=0.$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$: elliptic umbilic canonical integral function, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Referenced by:

Erratum (V1.0.1) for Equation (36.10.14)

Permalink:

http://dlmf.nist.gov/36.10.E14

Encodings:

pMML, png, TeX

Errata (effective with 1.0.1):

Originally appeared with $\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}$, rather than $\frac{\partial {\mathrm{\Psi }}^{(\mathrm{E})}}{\partial x}$:

$$3\left(\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial x}^2}-\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial y}^2}\right)+2\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}-x{\mathrm{\Psi }}^{(\mathrm{E})}=0.$$

See also:

Annotations for §36.10(iii), §36.10 and Ch.36

►

36.10.15 $$3\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{H})}}{{\partial x}^2}+\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial y}-x{\mathrm{\Psi }}^{(\mathrm{H})}=0,$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.10.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §36.10(iii), §36.10 and Ch.36

►

36.10.16 $$3\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{H})}}{{\partial y}^2}+\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}-y{\mathrm{\Psi }}^{(\mathrm{H})}=0.$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.10.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §36.10(iii), §36.10 and Ch.36

… ►

36.10.18 $$\mathrm{i}\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial z}=\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x\partial y}.$$

ⓘ

Symbols:

${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $\frac{\partial f}{\partial x}$: partial derivative of $f$ with respect to $x$ , $\partial x$: partial differential of $x$ , $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.10.E18

Encodings:

pMML, png, TeX

See also:

Annotations for §36.10(iv), §36.10 and Ch.36

…

4: 36.1 Special Notation

… ►The main functions covered in this chapter are cuspoid catastrophes ${\mathrm{\Phi }}_K(t;𝐱)$; umbilic catastrophes with codimension three ${\mathrm{\Phi }}^{(\mathrm{E})}(s,t;𝐱)$, ${\mathrm{\Phi }}^{(\mathrm{H})}(s,t;𝐱)$; canonical integrals ${\mathrm{\Psi }}_K\left(𝐱\right)$, ${\mathrm{\Psi }}^{(\mathrm{E})}\left(𝐱\right)$, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$; diffraction catastrophes ${\mathrm{\Psi }}_K(𝐱;k)$, ${\mathrm{\Psi }}^{(\mathrm{E})}(𝐱;k)$, ${\mathrm{\Psi }}^{(\mathrm{H})}(𝐱;k)$ generated by the catastrophes. …

5: 36.9 Integral Identities

§36.9 Integral Identities

… ►

36.9.8 $${\left|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,z\right)\right|}^2=8{\pi }^2{\left(\frac{2}{9}\right)}^{1/3}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{Ai}\left({\left(\frac{4}{3}\right)}^{1/3}(x+zv+3u^2)\right)\mathrm{Ai}\left({\left(\frac{4}{3}\right)}^{1/3}(y+zu+3v^2)\right)dudv.$$

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\int$: integral, $y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.9.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §36.9 and Ch.36

…

6: 36.11 Leading-Order Asymptotics

§36.11 Leading-Order Asymptotics

… ►

36.11.8 $${\mathrm{\Psi }}^{(\mathrm{H})}\left(0,0,z\right)=\frac{2\pi }{z}\left(1-\frac{\mathrm{i}}{\sqrt{3}}\exp \left(\frac{1}{27}\mathrm{i}{z}^3\right)+o\left(1\right)\right),$$ $z\to \pm \mathrm{\infty }$.

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\exp z$: exponential function, ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $o\left(x\right)$: order less than and $z$: real parameter

Permalink:

http://dlmf.nist.gov/36.11.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §36.11, §36.11 and Ch.36

7: 36.8 Convergent Series Expansions

§36.8 Convergent Series Expansions

… ►

36.8.3 $$\frac{3^{2/3}}{4{\pi }^2}{\mathrm{\Psi }}^{(\mathrm{H})}\left(3^{1/3}𝐱\right)=\mathrm{Ai}\left(x\right)\mathrm{Ai}\left(y\right)\sum _{n=0}^{\mathrm{\infty }}{(-3^{-1/3}\mathrm{i}z)}^n\frac{c_n(x)c_n(y)}{n!}+\mathrm{Ai}\left(x\right){\mathrm{Ai}}^{\prime }\left(y\right)\sum _{n=2}^{\mathrm{\infty }}{(-3^{-1/3}\mathrm{i}z)}^n\frac{c_n(x)d_n(y)}{n!}+{\mathrm{Ai}}^{\prime }\left(x\right)\mathrm{Ai}\left(y\right)\sum _{n=2}^{\mathrm{\infty }}{(-3^{-1/3}\mathrm{i}z)}^n\frac{d_n(x)c_n(y)}{n!}+{\mathrm{Ai}}^{\prime }\left(x\right){\mathrm{Ai}}^{\prime }\left(y\right)\sum _{n=1}^{\mathrm{\infty }}{(-3^{-1/3}\mathrm{i}z)}^n\frac{d_n(x)d_n(y)}{n!},$$

ⓘ

Symbols:

$\mathrm{Ai}\left(z\right)$: Airy function, $\pi$: the ratio of the circumference of a circle to its diameter, $!$: factorial (as in $n!$), ${\mathrm{\Psi }}^{(\mathrm{H})}\left(𝐱\right)$: hyperbolic umbilic canonical integral function, $\mathrm{i}$: imaginary unit, $y$: real parameter, $z$: real parameter, $m$: integer, $x$: real parameter, $c_n(t)$: coefficients and $d_n(t)$: coefficients

Referenced by:

§36.8

Permalink:

http://dlmf.nist.gov/36.8.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §36.8 and Ch.36

…

8: Errata

… ►

Scales were corrected in all figures. The interval $-8.4\le \frac{x-y}{\sqrt{2}}\le 8.4$ was replaced by $-12.0\le \frac{x-y}{\sqrt{2}}\le 12.0$ and $-12.7\le \frac{x+y}{\sqrt{2}}\le 4.2$ replaced by $-18.0\le \frac{x+y}{\sqrt{2}}\le 6.0$. All plots and interactive visualizations were regenerated to improve image quality.

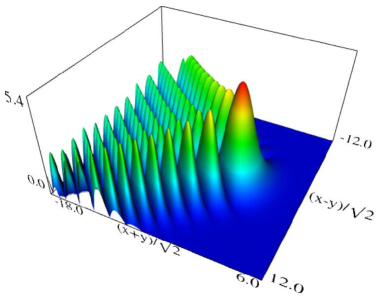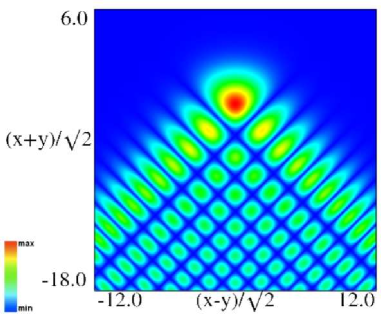
(a) Density plot.	(b) 3D plot.

Figure 36.3.9: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)|$.

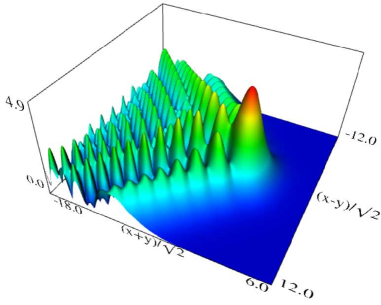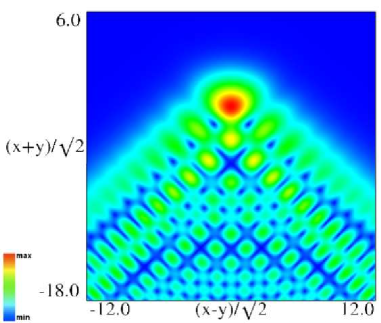
(a) Density plot.	(b) 3D plot.

Figure 36.3.10: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,1\right)|$.

(a) Density plot.	(b) 3D plot.

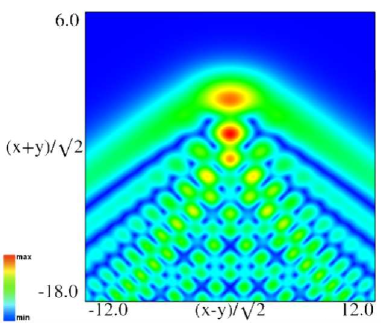
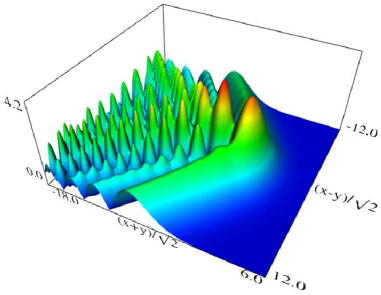
Figure 36.3.11: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,2\right)|$.

(a) Density plot.	(b) 3D plot.

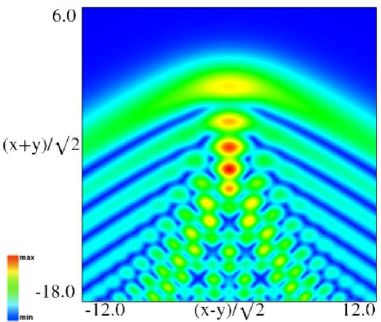
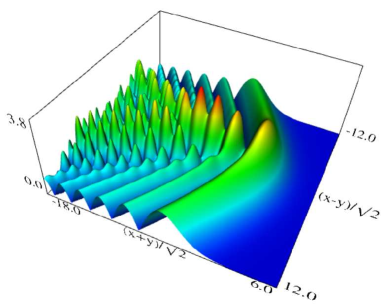
Figure 36.3.12: Modulus of hyperbolic umbilic canonical integral function $|{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,3\right)|$.

Reported 2016-09-12 by Dan Piponi.

►

The scaling error reported on 2016-09-12 by Dan Piponi also applied to contour and density plots for the phase of the hyperbolic umbilic canonical integrals. Scales were corrected in all figures. The interval $-8.4\le \frac{x-y}{\sqrt{2}}\le 8.4$ was replaced by $-12.0\le \frac{x-y}{\sqrt{2}}\le 12.0$ and $-12.7\le \frac{x+y}{\sqrt{2}}\le 4.2$ replaced by $-18.0\le \frac{x+y}{\sqrt{2}}\le 6.0$. All plots and interactive visualizations were regenerated to improve image quality.

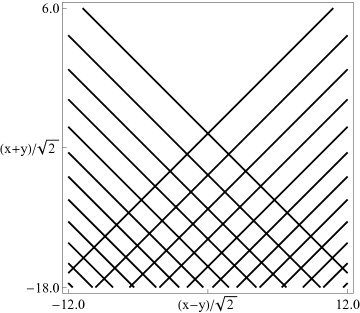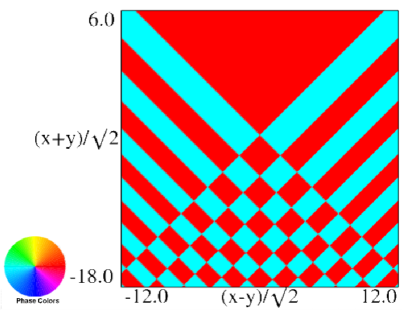(a) Contour plot.	(b) Density plot.

Figure 36.3.18: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,0\right)$.

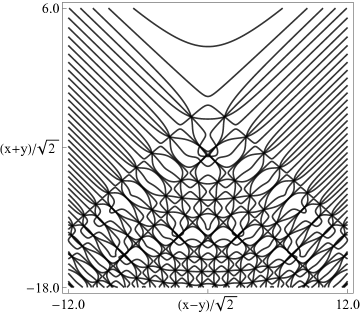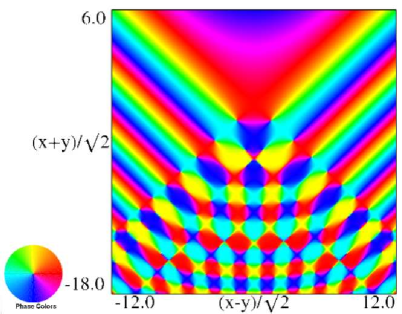(a) Contour plot.	(b) Density plot.

Figure 36.3.19: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,1\right)$.

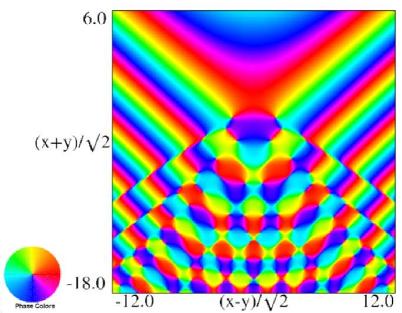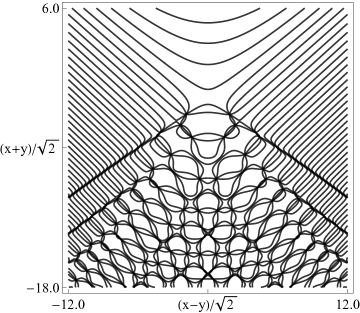
(a) Contour plot.	(b) Density plot.

Figure 36.3.20: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,2\right)$.

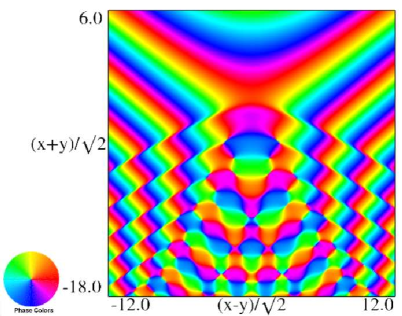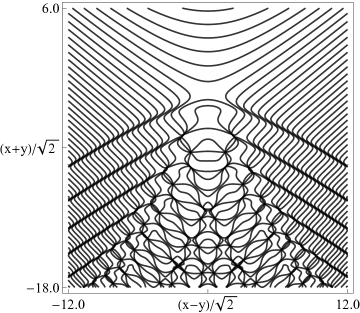
(a) Contour plot.	(b) Density plot.

Figure 36.3.21: Phase of hyperbolic umbilic canonical integral $\mathrm{ph}{\mathrm{\Psi }}^{(\mathrm{H})}\left(x,y,3\right)$.

Reported 2016-09-28.

… ►

36.10.14 $$3\left(\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial x}^2}-\frac{{\partial }^2{\mathrm{\Psi }}^{(\mathrm{E})}}{{\partial y}^2}\right)+2\mathrm{i}z\frac{\partial {\mathrm{\Psi }}^{(\mathrm{E})}}{\partial x}-x{\mathrm{\Psi }}^{(\mathrm{E})}=0$$

Originally this equation appeared with $\frac{\partial {\mathrm{\Psi }}^{(\mathrm{H})}}{\partial x}$ in the second term, rather than $\frac{\partial {\mathrm{\Psi }}^{(\mathrm{E})}}{\partial x}$.

Reported 2010-04-02.

…

9: 36.6 Scaling Relations

§36.6 Scaling Relations

…

10: 36.7 Zeros

… ►

§36.7(iv) Swallowtail and Hyperbolic Umbilic Canonical Integrals

►The zeros of these functions are curves in $𝐱=(x,y,z)$ space; see Nye (2007) for ${\mathrm{\Phi }}_3$ and Nye (2006) for ${\mathrm{\Phi }}^{(\mathrm{H})}$.