general%20lemniscatic%20case

SearchAdvancedHelp

(0.004 seconds)

11—20 of 556 matching pages

11: Staff

… ►

Daniel W. Lozier, General Editor, NIST (retired)

… ►

William P. Reinhardt, University of Washington, Chaps. 20, 22, 23

… ►

Peter L. Walker, American University of Sharjah, Chaps. 20, 22, 23

… ►

William P. Reinhardt, University of Washington, for Chaps. 20, 22, 23

… ►

Peter L. Walker, American University of Sharjah, for Chaps. 20, 22, 23

…

12: 23.4 Graphics

… ►

§23.4(i) Real Variables

►Line graphs of the Weierstrass functions $\mathrm{\wp }\left(x\right)$, $\zeta \left(x\right)$, and $\sigma \left(x\right)$, illustrating the lemniscatic and equianharmonic cases. … ►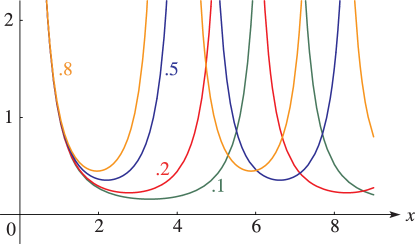

►►

Figure 23.4.1: $\mathrm{\wp }(x;g_2,0)$ for $0\le x\le 9$, $g_2$ = 0. …(Lemniscatic case.) Magnify

… ►

►►

Figure 23.4.3: $\zeta (x;g_2,0)$ for $0\le x\le 8$, $g_2$ = 0. …(Lemniscatic case.) Magnify

… ►

►►

Figure 23.4.5: $\sigma (x;g_2,0)$ for $-5\le x\le 5$, $g_2$ = 0. …(Lemniscatic case.) Magnify

…

13: 28.35 Tables

… ►

Blanch and Clemm (1965) includes values of ${\mathrm{Mc}}_n^{(2)}(x,\sqrt{q})$, $\mathrm{Mc}_n^{(2)}{}_{}{}^{\prime }(x,\sqrt{q})$ for $n=0(1)7$, $x=0(.02)1$; $n=8(1)15$, $x=0(.01)1$. Also ${\mathrm{Ms}}_n^{(2)}(x,\sqrt{q})$, $\mathrm{Ms}_n^{(2)}{}_{}{}^{\prime }(x,\sqrt{q})$ for $n=1(1)7$, $x=0(.02)1$; $n=8(1)15$, $x=0(.01)1$. In all cases $q=0(.05)1$. Precision is generally 7D. Approximate formulas and graphs are also included.

… ►

Ince (1932) includes eigenvalues $a_n$, $b_n$, and Fourier coefficients for $n=0$ or $1(1)6$, $q=0(1)10(2)20(4)40$; 7D. Also ${\mathrm{ce}}_n(x,q)$, ${\mathrm{se}}_n(x,q)$ for $q=0(1)10$, $x=1(1)90$, corresponding to the eigenvalues in the tables; 5D. Notation: $a_n={\mathrm{𝑏𝑒}}_n-2q$, $b_n={\mathrm{𝑏𝑜}}_n-2q$.

►

Kirkpatrick (1960) contains tables of the modified functions ${\mathrm{Ce}}_n(x,q)$, ${\mathrm{Se}}_{n+1}(x,q)$ for $n=0(1)5$, $q=1(1)20$, $x=0.1(.1)1$; 4D or 5D.

►

National Bureau of Standards (1967) includes the eigenvalues $a_n\left(q\right)$, $b_n\left(q\right)$ for $n=0(1)3$ with $q=0(.2)20(.5)37(1)100$, and $n=4(1)15$ with $q=0(2)100$; Fourier coefficients for ${\mathrm{ce}}_n(x,q)$ and ${\mathrm{se}}_n(x,q)$ for $n=0(1)15$, $n=1(1)15$, respectively, and various values of $q$ in the interval $[0,100]$; joining factors $g_{e,n}(\sqrt{q})$, $f_{e,n}(\sqrt{q})$ for $n=0(1)15$ with $q=0(.5\text{ to }10)100$ (but in a different notation). Also, eigenvalues for large values of $q$. Precision is generally 8D.

… ►

Zhang and Jin (1996, pp. 521–532) includes the eigenvalues $a_n\left(q\right)$, $b_{n+1}\left(q\right)$ for $n=0(1)4$, $q=0(1)50$; $n=0(1)20$ ($a$’s) or 19 ($b$’s), $q=1,3,5,10,15,25,50(50)200$. Fourier coefficients for ${\mathrm{ce}}_n(x,10)$, ${\mathrm{se}}_{n+1}(x,10)$, $n=0(1)7$. Mathieu functions ${\mathrm{ce}}_n(x,10)$, ${\mathrm{se}}_{n+1}(x,10)$, and their first $x$-derivatives for $n=0(1)4$, $x=0(5^{\circ }){90}^{\circ }$. Modified Mathieu functions ${\mathrm{Mc}}_n^{(j)}(x,\sqrt{10})$, ${\mathrm{Ms}}_{n+1}^{(j)}(x,\sqrt{10})$, and their first $x$-derivatives for $n=0(1)4$, $j=1,2$, $x=0(.2)4$. Precision is mostly 9S.

…

14: Foreword

… ►Particular attention is called to the generous support of the National Science Foundation, which made possible the participation of experts from academia and research institutes worldwide. … ►November 20, 2009 …

15: Publications

… ►

Using Numerical Grid Generation to Facilitate 3D Visualization of Complicated Mathematical Functions, Technical Report NISTIR 6413 (November 1999), National Institute of Standards and Technology.

… ►

From 2D to 3D: Numerical Grid Generation and the Visualization of Complex Surfaces, Proceedings of the 7th International Conference on Numerical Grid Generation in Computational Field Simulations, Whistler, British Columbia, Canada, September 25-28, 2000.

… ►

Boundary/Contour Fitted Grid Generation for Effective Visualizations in a Digital Library of Mathematical Functions, Proceedings of the 9th International Conference on Numerical Grid Generation in Computational Field Simulations, San Jose, June 11–18, 2005. pp. 61–71.

… ►

Methods of Relevance Ranking and Hit-content Generation in Math Search, Proceedings of Mathematical Knowledge Management (MKM2007), RISC, Hagenberg, Austria, June 27–30, 2007.

… ►

NIST’s Digital Library of Mathematial Functions, Physics Today 71, 2, 48 (2018), pp. 48–53.

16: 16.24 Physical Applications

§16.24 Physical Applications

►

§16.24(i) Random Walks

►Generalized hypergeometric functions and Appell functions appear in the evaluation of the so-called Watson integrals which characterize the simplest possible lattice walks. … ►

§16.24(iii) $\mathit{3}j$, $\mathit{6}j$, and $\mathit{9}j$ Symbols

… ►Lastly, special cases of the $\mathit{9}j$ symbols are ${}_5{}^{}F_4^{}$ functions with unit argument. …

17: 32.8 Rational Solutions

… ►More generally, … ►In the general case assume $\gamma \delta \ne 0$, so that as in §32.2(ii) we may set $\gamma =1$ and $\delta =-1$. … ►In general, ${\text{P}}_{\text{IV}}$ has rational solutions iff either … ►In the general case assume $\delta \ne 0$, so that as in §32.2(ii) we may set $\delta =-\frac{1}{2}$. … ►In the general case, ${\text{P}}_{\text{VI}}$ has rational solutions if …

18: 14.29 Generalizations

§14.29 Generalizations

… ►

14.29.1 $$\left(1-z^2\right)\frac{d^{2}w}{{dz}^2}-2z\frac{dw}{dz}+\left(\nu (\nu +1)-\frac{{\mu }_1^2}{2(1-z)}-\frac{{\mu }_2^2}{2(1+z)}\right)w=0$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $z$: complex variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.29

Permalink:

http://dlmf.nist.gov/14.29.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §14.29 and Ch.14

►are called Generalized Associated Legendre Functions. As in the case of (14.21.1), the solutions are hypergeometric functions, and (14.29.1) reduces to (14.21.1) when ${\mu }_1={\mu }_2=\mu$. … …

19: Bibliography N

… ►

On an integral transform involving a class of Mathieu functions. SIAM J. Math. Anal. 20 (6), pp. 1500–1513.

ⓘ

External Links:

ISSN 0036-1410, Document, MathReview (K. C. Gupta), ZentralBlatt

Referenced by:

§28.26(ii).

Encodings:

BibTeX

… ►

Reduction and evaluation of elliptic integrals. Math. Comp. 20 (94), pp. 223–231.

ⓘ

External Links:

FullText, MathReview (I. A. Stegun), ZentralBlatt

Referenced by:

§19.37(iv).

Encodings:

BibTeX

… ►

Generalization of Binet’s Gamma function formulas. Integral Transforms Spec. Funct. 24 (8), pp. 597–606.

ⓘ

External Links:

ISSN 1065-2469, Document, FullText, MathReview (Daniele Ritelli), ZentralBlatt

Referenced by:

§5.11(i), §5.11(i).

Encodings:

BibTeX

… ►

A table of integrals of the error functions. J. Res. Nat. Bur. Standards Sect B. 73B, pp. 1–20.

ⓘ

Notes:

See for additions and corrections same journal, Sect. B 75, 149–163 (1975)

External Links:

MathReview, ZentralBlatt

Referenced by:

§7.14(iii), §7.21, §7.7(iii).

Encodings:

BibTeX

… ►

The asymptotic behavior of the general real solution of the third Painlevé equation. Dokl. Akad. Nauk SSSR 283 (5), pp. 1161–1165 (Russian).

ⓘ

Notes:

In Russian. English translation: Sov. Math., Dokl. 30(1988), no. 8, pp. 666–668.

External Links:

ISSN 0002-3264, MathReview (Vojislav Marić), ZentralBlatt

Referenced by:

§32.11(iv).

Encodings:

BibTeX

…

20: 8.16 Generalizations

§8.16 Generalizations

►For a generalization of the incomplete gamma function, including asymptotic approximations, see Chaudhry and Zubair (1994, 2001) and Chaudhry et al. (1996). Other generalizations are considered in Guthmann (1991) and Paris (2003).