as functions of parameters

SearchAdvancedHelp

(0.015 seconds)

1—10 of 376 matching pages

1: 31.13 Asymptotic Approximations

§31.13 Asymptotic Approximations

…

2: 28.27 Addition Theorems

… ►Addition theorems provide important connections between Mathieu functions with different parameters and in different coordinate systems. …

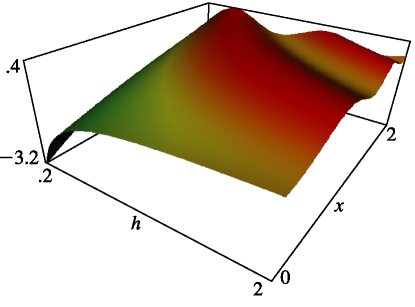
3: 28.21 Graphics

§28.21 Graphics

►

Radial Mathieu Functions: Surfaces

… ►

►

►

Figure 28.21.6: ${\mathrm{Ms}}_1^{(2)}(x,h)$ for $0.2\le h\le 2$, $0\le x\le 2$. Magnify 3D Help

4: 8.17 Incomplete Beta Functions

… ►

8.17.4 $$I_x(a,b)=1-I_{1-x}(b,a).$$

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter and $x$: variable

A&S Ref:

6.6.3 (Symmetry relation)

Referenced by:

§8.17(v), §8.18(i)

Permalink:

http://dlmf.nist.gov/8.17.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(i), §8.17 and Ch.8

… ►

8.17.13 $$(a+b)I_x(a,b)=a{I}_x(a+1,b)+b{I}_x(a,b+1),$$

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter and $x$: variable

A&S Ref:

6.6.7

Permalink:

http://dlmf.nist.gov/8.17.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(iv), §8.17 and Ch.8

… ►

8.17.16 $$a{I}_x(a+1,b)=(a+cx)I_x(a,b)-cx{I}_x(a-1,b),$$

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter, $x$: variable and $c$

Permalink:

http://dlmf.nist.gov/8.17.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(iv), §8.17 and Ch.8

… ►

8.17.20 $$I_x(a,b)=I_x(a+1,b)+\frac{x^a{(x^{\prime })}^b}{a\mathrm{B}(a,b)},$$

ⓘ

Symbols:

$\mathrm{B}(a,b)$: beta function, $I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter, $x$: variable and $x^{\prime }$

Permalink:

http://dlmf.nist.gov/8.17.E20

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(iv), §8.17 and Ch.8

►

8.17.21 $$I_x(a,b)=I_x(a,b+1)-\frac{x^a{(x^{\prime })}^b}{b\mathrm{B}(a,b)}.$$

ⓘ

Symbols:

$\mathrm{B}(a,b)$: beta function, $I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter, $x$: variable and $x^{\prime }$

Permalink:

http://dlmf.nist.gov/8.17.E21

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(iv), §8.17 and Ch.8

…

5: 16.22 Asymptotic Expansions

… ►For asymptotic expansions of Meijer $G$-functions with large parameters see Fields (1973, 1983).

6: 33.13 Complex Variable and Parameters

§33.13 Complex Variable and Parameters

… ►

33.13.1 $$C_{\mathrm{\ell }}\left(\eta \right)=2^{\mathrm{\ell }}{\mathrm{e}}^{\mathrm{i}{\sigma }_{\mathrm{\ell }}\left(\eta \right)-(\pi \eta /2)}\mathrm{\Gamma }\left(\mathrm{\ell }+1-\mathrm{i}\eta \right)/\mathrm{\Gamma }\left(2\mathrm{\ell }+2\right),$$

ⓘ

Symbols:

$C_{\mathrm{\ell }}\left(\eta \right)$: normalizing constant for Coulomb radial functions, ${\sigma }_{\mathrm{\ell }}\left(\eta \right)$: Coulomb phase shift, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{\ell }$: nonnegative integer and $\eta$: real parameter

Permalink:

http://dlmf.nist.gov/33.13.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §33.13 and Ch.33

… ►

33.13.2 $$R_{\mathrm{\ell }}=(2\mathrm{\ell }+1)C_{\mathrm{\ell }}\left(\eta \right)/C_{\mathrm{\ell }-1}\left(\eta \right).$$

ⓘ

Symbols:

$C_{\mathrm{\ell }}\left(\eta \right)$: normalizing constant for Coulomb radial functions, $\mathrm{\ell }$: nonnegative integer, $\eta$: real parameter and $R_{\mathrm{\ell }}$: factor

Permalink:

http://dlmf.nist.gov/33.13.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §33.13 and Ch.33

…

7: 33.22 Particle Scattering and Atomic and Molecular Spectra

… ►

$𝗄$ Scaling

… ►

$Z$ Scaling

… ►

$\mathrm{i}𝗄$ Scaling

… ►

§33.22(iii) Conversions Between Variables

… ►

§33.22(vii) Complex Variables and Parameters

…

8: 20.1 Special Notation

… ► ►►►

$m$, $n$	integers.
…
$q$ $(\in ℂ)$	the nome, $q={\mathrm{e}}^{\mathrm{i}\pi \tau }$, . Since $\tau$ is not a single-valued function of $q$, it is assumed that $\tau$ is known, even when $q$ is specified. Most applications concern the rectangular case $\mathrm{\Re }\tau =0$, $\mathrm{\Im }\tau >0$, so that and $\tau$ and $q$ are uniquely related.
…

…

9: Bibliography U

… ►

Integrals with a large parameter: Legendre functions of large degree and fixed order. Math. Proc. Cambridge Philos. Soc. 95 (2), pp. 367–380.

ⓘ

External Links:

ISSN 0305-0041, Document, MathReview (Roderick Wong), ZentralBlatt

Referenced by:

§14.26.

Encodings:

BibTeX

…

10: 31.1 Special Notation

… ►Sometimes the parameters are suppressed.