Pearcey integral

SearchAdvancedHelp

(0.002 seconds)

1—10 of 13 matching pages

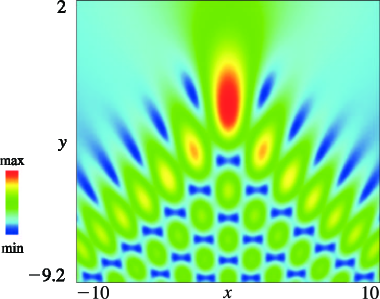
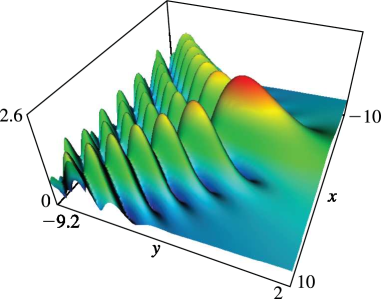
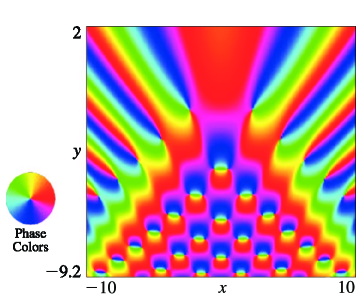
1: 36.2 Catastrophes and Canonical Integrals

… ► ${\mathrm{\Psi }}_2$ is the Pearcey integral (Pearcey (1946)): ►

36.2.14 $${\mathrm{\Psi }}_2\left(𝐱\right)=P(x_2,x_1)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\exp \left(\mathrm{i}(t^4+x_2{t}^2+x_{1}t)\right)dt.$$

ⓘ

Symbols:

${\mathrm{\Psi }}_K\left(𝐱\right)$: canonical integral function, $dx$: differential of $x$ , $\exp z$: exponential function, $\mathrm{i}$: imaginary unit, $\int$: integral, $t$: variable and $x_{\mathrm{i}}$: real parameter

Referenced by:

§36.12(i)

Permalink:

http://dlmf.nist.gov/36.2.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §36.2(ii), §36.2 and Ch.36

… ► …

2: 36.7 Zeros

… ► … ►

Table 36.7.1: Zeros of cusp diffraction catastrophe to 5D.

► ►►

Zeros $\left\{\genfrac{}{}{0.0pt}{}{x}{y}\right\}$ inside, and zeros $\left[\genfrac{}{}{0.0pt}{}{x}{y}\right]$ outside, the cusp $x^2=\frac{8}{27}{|y|}^3$.
…

►

…

3: 36.3 Visualizations of Canonical Integrals

… ►

► ►►

…

►

Figure 36.3.1: Modulus of Pearcey integral $|{\mathrm{\Psi }}_2\left(x,y\right)|$. Magnify 3D Help

… ►

► ►►

…

►

Figure 36.3.13: Phase of Pearcey integral $\mathrm{ph}{\mathrm{\Psi }}_2\left(x,y\right)$. Magnify

…

4: 36.6 Scaling Relations

§36.6 Scaling Relations

…

5: 36.9 Integral Identities

§36.9 Integral Identities

…

6: 36.5 Stokes Sets

… ►

§36.5(ii) Cuspoids

… ►

§36.5(iv) Visualizations

…

7: 36.11 Leading-Order Asymptotics

§36.11 Leading-Order Asymptotics

…

8: 36.8 Convergent Series Expansions

§36.8 Convergent Series Expansions

…

9: 36.12 Uniform Approximation of Integrals

… ►For example, the diffraction catastrophe ${\mathrm{\Psi }}_2(x,y;k)$ defined by (36.2.10), and corresponding to the Pearcey integral (36.2.14), can be approximated by the Airy function ${\mathrm{\Psi }}_1\left(\xi (x,y;k)\right)$ when $k$ is large, provided that $x$ and $y$ are not small. … ►For further information concerning integrals with several coalescing saddle points see Arnol’d et al. (1988), Berry and Howls (1993, 1994), Bleistein (1967), Duistermaat (1974), Ludwig (1966), Olde Daalhuis (2000), and Ursell (1972, 1980).

10: 36.10 Differential Equations

… ► $K=2$, cusp: …