Olver associated Legendre function

SearchAdvancedHelp

(0.016 seconds)

1—10 of 42 matching pages

1: 14.21 Definitions and Basic Properties

… ►

14.21.1 $$\left(1-z^2\right)\frac{d^{2}w}{{dz}^2}-2z\frac{dw}{dz}+\left(\nu (\nu +1)-\frac{{\mu }^2}{1-z^2}\right)w=0.$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $z$: complex variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.1.1

Referenced by:

§14.21(ii), §14.29, 2nd item

Permalink:

http://dlmf.nist.gov/14.21.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §14.21(i), §14.21 and Ch.14

…

2: 14.24 Analytic Continuation

… ►

14.24.1 $$P_{\nu }^{-\mu }\left(z{\mathrm{e}}^{s\pi \mathrm{i}}\right)={\mathrm{e}}^{s\nu \pi \mathrm{i}}{P}_{\nu }^{-\mu }\left(z\right)+\frac{2\mathrm{i}\sin \left(\left(\nu +\frac{1}{2}\right)s\pi \right){\mathrm{e}}^{-s\pi \mathrm{i}/2}}{\cos \left(\nu \pi \right)\mathrm{\Gamma }\left(\mu -\nu \right)}{𝑸}_{\nu }^{\mu }\left(z\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $z$: complex variable, $\mu$: general order, $\nu$: general degree and $s$: arbitrary integer

Referenced by:

§14.24, §14.24

Permalink:

http://dlmf.nist.gov/14.24.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §14.24 and Ch.14

►

14.24.2 $${𝑸}_{\nu }^{\mu }\left(z{\mathrm{e}}^{s\pi \mathrm{i}}\right)={(-1)}^s{\mathrm{e}}^{-s\nu \pi \mathrm{i}}{𝑸}_{\nu }^{\mu }\left(z\right),$$

ⓘ

Symbols:

${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable, $\mu$: general order, $\nu$: general degree and $s$: arbitrary integer

Referenced by:

§14.23, §14.24

Permalink:

http://dlmf.nist.gov/14.24.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §14.24 and Ch.14

… ►

14.24.4 $${𝑸}_{\nu ,s}^{\mu }\left(z\right)={\mathrm{e}}^{-s\mu \pi \mathrm{i}}{𝑸}_{\nu }^{\mu }\left(z\right)-\frac{\pi \mathrm{i}\sin \left(s\mu \pi \right)}{\sin \left(\mu \pi \right)\mathrm{\Gamma }\left(\nu -\mu +1\right)}{P}_{\nu }^{-\mu }\left(z\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $z$: complex variable, $\mu$: general order, $\nu$: general degree and $s$: arbitrary integer

Referenced by:

§14.24

Permalink:

http://dlmf.nist.gov/14.24.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §14.24 and Ch.14

…

3: 14.12 Integral Representations

… ►

14.12.9 $${𝑸}_n^m\left(x\right)=\frac{1}{n!}{\int }_0^u{\left(x-{\left(x^2-1\right)}^{1/2}\cosh t\right)}^n\cosh \left(mt\right)dt,$$

ⓘ

Symbols:

${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\cosh z$: hyperbolic cosine function, $\int$: integral, $x$: real variable, $m$: nonnegative integer, $n$: nonnegative integer and $u$

Permalink:

http://dlmf.nist.gov/14.12.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12 and Ch.14

… ►

14.12.11 $${𝑸}_n^m\left(x\right)=\frac{{\left(x^2-1\right)}^{m/2}}{2^{n+1}n!}{\int }_{-1}^1\frac{{\left(1-t^2\right)}^n}{{(x-t)}^{n+m+1}}dt,$$

ⓘ

Symbols:

${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, $x$: real variable, $m$: nonnegative integer and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/14.12.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12 and Ch.14

►

14.12.12 $${𝑸}_n^m\left(x\right)=\frac{1}{(n-m)!}{P}_n^m\left(x\right){\int }_x^{\mathrm{\infty }}\frac{dt}{\left(t^2-1\right){\left(P_n^m\left(t\right)\right)}^2},$$ $n\ge m$.

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, $x$: real variable, $m$: nonnegative integer and $n$: nonnegative integer

Referenced by:

§14.17(i)

Permalink:

http://dlmf.nist.gov/14.12.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12 and Ch.14

… ►

14.12.13 $${𝑸}_n\left(x\right)=\frac{1}{2(n!)}{\int }_{-1}^1\frac{P_n\left(t\right)}{x-t}dt.$$

ⓘ

Symbols:

$P_n\left(x\right)$: Legendre polynomial, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable and $n$: nonnegative integer

A&S Ref:

8.8.3 (modified)

Permalink:

http://dlmf.nist.gov/14.12.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12(ii), §14.12 and Ch.14

… ►

14.12.14 $${𝑸}_n\left(x\right)=\frac{1}{n!}{\int }_0^{\mathrm{\infty }}\frac{dt}{{\left(x+{(x^2-1)}^{1/2}\cosh t\right)}^{n+1}}.$$

ⓘ

Symbols:

$dx$: differential of $x$ , $!$: factorial (as in $n!$), $\cosh z$: hyperbolic cosine function, $\int$: integral, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/14.12.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12(ii), §14.12 and Ch.14

…

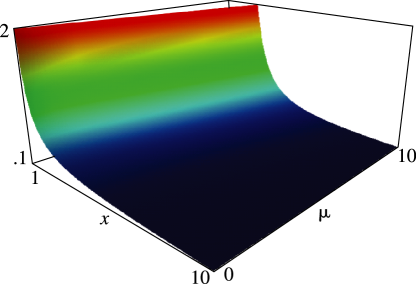
4: 14.4 Graphics

… ►

§14.4(i) Ferrers Functions: 2D Graphs

… ►

§14.4(ii) Ferrers Functions: 3D Surfaces

… ►

§14.4(iii) Associated Legendre Functions: 2D Graphs

… ►

§14.4(iv) Associated Legendre Functions: 3D Surfaces

… ►

►

►

Figure 14.4.32: ${𝑸}_0^{\mu }\left(x\right)$, $0\le \mu \le 10$, . Magnify 3D Help

5: 14.19 Toroidal (or Ring) Functions

… ►

14.19.3 $${𝑸}_{\nu -\frac{1}{2}}^{\mu }\left(\cosh \xi \right)=\frac{{\pi }^{1/2}{\left(1-{\mathrm{e}}^{-2\xi }\right)}^{\mu }}{{\mathrm{e}}^{(\nu +(1/2))\xi }}𝐅(\mu +\frac{1}{2},\nu +\mu +\frac{1}{2};\nu +1;{\mathrm{e}}^{-2\xi }).$$

ⓘ

Symbols:

${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\cosh z$: hyperbolic cosine function, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\mu$: general order, $\nu$: general degree and $\xi >0$: variable

Permalink:

http://dlmf.nist.gov/14.19.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §14.19(ii), §14.19 and Ch.14

… ►

14.19.5 $${𝑸}_{n-\frac{1}{2}}^m\left(\cosh \xi \right)=\frac{\mathrm{\Gamma }\left(n+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(n+m+\frac{1}{2}\right)\mathrm{\Gamma }\left(n-m+\frac{1}{2}\right)}{\int }_0^{\mathrm{\infty }}\frac{\cosh \left(mt\right)}{{(\cosh \xi +\cosh t\sinh \xi )}^{n+(1/2)}}dt,$$ .

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $dx$: differential of $x$ , $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\int$: integral, $m$: nonnegative integer, $n$: nonnegative integer and $\xi >0$: variable

A&S Ref:

8.11.4 (modified and corrected)

Permalink:

http://dlmf.nist.gov/14.19.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §14.19(iii), §14.19 and Ch.14

… ►

14.19.6 $${𝑸}_{-\frac{1}{2}}^{\mu }\left(\cosh \xi \right)+2\sum _{n=1}^{\mathrm{\infty }}\frac{\mathrm{\Gamma }\left(\mu +n+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(\mu +\frac{1}{2}\right)}{𝑸}_{n-\frac{1}{2}}^{\mu }\left(\cosh \xi \right)\cos \left(n\varphi \right)=\frac{{\left(\frac{1}{2}\pi \right)}^{1/2}{\left(\sinh \xi \right)}^{\mu }}{{\left(\cosh \xi -\cos \varphi \right)}^{\mu +(1/2)}},$$ $\mathrm{\Re }\mu >-\frac{1}{2}$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\mathrm{\Re }$: real part, $n$: nonnegative integer, $\mu$: general order and $\xi >0$: variable

Permalink:

http://dlmf.nist.gov/14.19.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §14.19(iv), §14.19 and Ch.14

… ►

14.19.7 $$P_{n-\frac{1}{2}}^m\left(\cosh \xi \right)=\frac{\mathrm{\Gamma }\left(n+m+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(n-m+\frac{1}{2}\right)}{\left(\frac{2}{\pi \sinh \xi }\right)}^{1/2}{𝑸}_{m-\frac{1}{2}}^n\left(\coth \xi \right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cosh z$: hyperbolic cosine function, $\coth z$: hyperbolic cotangent function, $\sinh z$: hyperbolic sine function, $m$: nonnegative integer, $n$: nonnegative integer and $\xi >0$: variable

Permalink:

http://dlmf.nist.gov/14.19.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §14.19(v), §14.19 and Ch.14

►

14.19.8 $${𝑸}_{n-\frac{1}{2}}^m\left(\cosh \xi \right)=\frac{\mathrm{\Gamma }\left(m-n+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(m+n+\frac{1}{2}\right)}{\left(\frac{\pi }{2\sinh \xi }\right)}^{1/2}{P}_{m-\frac{1}{2}}^n\left(\coth \xi \right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cosh z$: hyperbolic cosine function, $\coth z$: hyperbolic cotangent function, $\sinh z$: hyperbolic sine function, $m$: nonnegative integer, $n$: nonnegative integer and $\xi >0$: variable

Permalink:

http://dlmf.nist.gov/14.19.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §14.19(v), §14.19 and Ch.14

6: 14.9 Connection Formulas

… ►

14.9.12 $$\cos \left(\nu \pi \right)P_{\nu }^{-\mu }\left(x\right)=-\frac{{𝑸}_{\nu }^{\mu }\left(x\right)}{\mathrm{\Gamma }\left(\mu -\nu \right)}+\frac{{𝑸}_{-\nu -1}^{\mu }\left(x\right)}{\mathrm{\Gamma }\left(\nu +\mu +1\right)}.$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $x$: real variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.2.2 (modified)

Referenced by:

§14.20(i), §14.8(ii), §14.8(iii)

Permalink:

http://dlmf.nist.gov/14.9.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §14.9(iii), §14.9 and Ch.14

… ►

14.9.14 $${𝑸}_{\nu }^{-\mu }\left(x\right)={𝑸}_{\nu }^{\mu }\left(x\right),$$

ⓘ

Symbols:

${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $x$: real variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.2.6 (modified)

Referenced by:

§14.23, §14.9(iv)

Permalink:

http://dlmf.nist.gov/14.9.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §14.9(iii), §14.9 and Ch.14

►

14.9.15 $$\frac{2\sin \left(\mu \pi \right)}{\pi }{𝑸}_{\nu }^{\mu }\left(x\right)=\frac{P_{\nu }^{\mu }\left(x\right)}{\mathrm{\Gamma }\left(\nu +\mu +1\right)}-\frac{P_{\nu }^{-\mu }\left(x\right)}{\mathrm{\Gamma }\left(\nu -\mu +1\right)}.$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\sin z$: sine function, $x$: real variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.2.5 (modified)

Permalink:

http://dlmf.nist.gov/14.9.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §14.9(iii), §14.9 and Ch.14

… ►

14.9.16 $${𝑸}_{\nu }^{\mu }\left(x\right)={\left(\frac{1}{2}\pi \right)}^{1/2}{\left(x^2-1\right)}^{-1/4}{P}_{-\mu -(1/2)}^{-\nu -(1/2)}\left(x{\left(x^2-1\right)}^{-1/2}\right).$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $x$: real variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.2.7 (modified)

Referenced by:

§14.19(v), §14.21(iii), §14.9(iv)

Permalink:

http://dlmf.nist.gov/14.9.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §14.9(iv), §14.9 and Ch.14

… ►

14.9.17 $$P_{\nu }^{\mu }\left(x\right)={(2/\pi )}^{1/2}{\left(x^2-1\right)}^{-1/4}{𝑸}_{-\mu -(1/2)}^{\nu +(1/2)}\left(x{\left(x^2-1\right)}^{-1/2}\right).$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.19(v), §14.9(iv)

Permalink:

http://dlmf.nist.gov/14.9.E17

Encodings:

pMML, png, TeX

See also:

Annotations for §14.9(iv), §14.9 and Ch.14

7: 14.25 Integral Representations

… ►

14.25.2 $${𝑸}_{\nu }^{\mu }\left(z\right)=\frac{{\pi }^{1/2}{\left(z^2-1\right)}^{\mu /2}}{2^{\mu }\mathrm{\Gamma }\left(\mu +\frac{1}{2}\right)\mathrm{\Gamma }\left(\nu -\mu +1\right)}{\int }_0^{\mathrm{\infty }}\frac{{(\sinh t)}^{2\mu }}{{\left(z+{(z^2-1)}^{1/2}\cosh t\right)}^{\nu +\mu +1}}dt,$$ $\mathrm{\Re }\left(\nu +1\right)>\mathrm{\Re }\mu >-\frac{1}{2}$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\int$: integral, $\mathrm{\Re }$: real part, $z$: complex variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.25

Permalink:

http://dlmf.nist.gov/14.25.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §14.25 and Ch.14

…

8: 14.3 Definitions and Hypergeometric Representations

… ►

14.3.6

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\mu$: general order, $\nu$: general degree and : real variable

Referenced by:

§14.21(i), §14.21(iii), §14.3(ii), §14.3(iv), §15.9(iv)

Permalink:

http://dlmf.nist.gov/14.3.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §14.3(ii), §14.3(ii), §14.3 and Ch.14

… ►

14.3.8

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $m$: nonnegative integer, $\nu$: general degree and : real variable

Referenced by:

§14.3(ii)

Permalink:

http://dlmf.nist.gov/14.3.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §14.3(ii), §14.3(ii), §14.3 and Ch.14

… ►

14.3.10

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $Q_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the second kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mu$: general order, $\nu$: general degree and : real variable

Referenced by:

§14.20(i), §14.21(i), §14.21(iii), §14.6(i)

Permalink:

http://dlmf.nist.gov/14.3.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §14.3(ii), §14.3(ii), §14.3 and Ch.14

… ►

14.3.19

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\mu$: general order, $\nu$: general degree and : real variable

Permalink:

http://dlmf.nist.gov/14.3.E19

Encodings:

pMML, png, TeX

See also:

Annotations for §14.3(iii), §14.3 and Ch.14

►

14.3.20

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $\sin z$: sine function, $\mu$: general order, $\nu$: general degree and : real variable

A&S Ref:

8.1.6 (modified)

Referenced by:

§14.21(iii), §14.3(iii)

Permalink:

http://dlmf.nist.gov/14.3.E20

Encodings:

pMML, png, TeX

See also:

Annotations for §14.3(iii), §14.3 and Ch.14

…

9: 14.23 Values on the Cut

… ►

14.23.2 $${𝑸}_{\nu }^{\mu }\left(x\pm \mathrm{i}0\right)=\frac{{\mathrm{e}}^{\pm \mu \pi \mathrm{i}/2}}{\mathrm{\Gamma }\left(\nu +\mu +1\right)}\left({𝖰}_{\nu }^{\mu }\left(x\right)\mp \frac{1}{2}\pi \mathrm{i}{𝖯}_{\nu }^{\mu }\left(x\right)\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, : Ferrers function of the first kind, : Ferrers function of the second kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.23

Permalink:

http://dlmf.nist.gov/14.23.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §14.23 and Ch.14

… ►

14.23.3 $${𝑸}_{\nu }^{\mu }\left(x\pm \mathrm{i}0\right)=\frac{{\mathrm{e}}^{\mp \nu \pi \mathrm{i}/2}{\pi }^{3/2}{\left(1-x^2\right)}^{\mu /2}}{2^{\nu +1}}\left(\frac{x𝐅(\frac{1}{2}\mu -\frac{1}{2}\nu +\frac{1}{2},\frac{1}{2}\nu +\frac{1}{2}\mu +1;\frac{3}{2};x^2)}{\mathrm{\Gamma }\left(\frac{1}{2}\nu -\frac{1}{2}\mu +\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\nu +\frac{1}{2}\mu +\frac{1}{2}\right)}\mp \mathrm{i}\frac{𝐅(\frac{1}{2}\mu -\frac{1}{2}\nu ,\frac{1}{2}\nu +\frac{1}{2}\mu +\frac{1}{2};\frac{1}{2};x^2)}{\mathrm{\Gamma }\left(\frac{1}{2}\nu -\frac{1}{2}\mu +1\right)\mathrm{\Gamma }\left(\frac{1}{2}\nu +\frac{1}{2}\mu +1\right)}\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $𝐅(a,b;c;z)$ or $𝐅(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}𝐅_1^{}(a,b;c;z)$ Olver’s hypergeometric function, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.23

Permalink:

http://dlmf.nist.gov/14.23.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §14.23 and Ch.14

… ►

14.23.5 $${𝖰}_{\nu }^{\mu }\left(x\right)=\frac{1}{2}\mathrm{\Gamma }\left(\nu +\mu +1\right)\left({\mathrm{e}}^{-\mu \pi \mathrm{i}/2}{𝑸}_{\nu }^{\mu }\left(x+\mathrm{i}0\right)+{\mathrm{e}}^{\mu \pi \mathrm{i}/2}{𝑸}_{\nu }^{\mu }\left(x-\mathrm{i}0\right)\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, : Ferrers function of the second kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $x$: real variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.3.4 (modified)

Referenced by:

§14.23

Permalink:

http://dlmf.nist.gov/14.23.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §14.23 and Ch.14

… ►

14.23.6 $${𝖰}_{\nu }^{\mu }\left(x\right)={\mathrm{e}}^{\mp \mu \pi \mathrm{i}/2}\mathrm{\Gamma }\left(\nu +\mu +1\right){𝑸}_{\nu }^{\mu }\left(x\pm \mathrm{i}0\right)\pm \frac{1}{2}\pi \mathrm{i}{\mathrm{e}}^{\pm \mu \pi \mathrm{i}/2}{P}_{\nu }^{\mu }\left(x\pm \mathrm{i}0\right).$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, : Ferrers function of the second kind, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.23, §14.23

Permalink:

http://dlmf.nist.gov/14.23.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §14.23 and Ch.14

…

10: 14.8 Behavior at Singularities

… ►

14.8.9 $${𝑸}_{\nu }\left(x\right)=-\frac{\ln \left(x-1\right)}{2\mathrm{\Gamma }\left(\nu +1\right)}+\frac{\frac{1}{2}\ln 2-\gamma -\psi \left(\nu +1\right)}{\mathrm{\Gamma }\left(\nu +1\right)}+O\left(\left(x-1\right)\ln \left(x-1\right)\right),$$ $\nu \ne -1,-2,-3,\mathrm{\dots }$,

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\gamma$: Euler’s constant, $\psi \left(z\right)$: psi (or digamma) function, $\ln z$: principal branch of logarithm function, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable and $\nu$: general degree

Referenced by:

Erratum (V1.1.5) for Equation (14.8.9)

Permalink:

http://dlmf.nist.gov/14.8.E9

Encodings:

pMML, png, TeX

Correction (effective with 1.1.5):

The symbol $O\left(x-1\right)$ has been corrected to be $O\left(\left(x-1\right)\ln \left(x-1\right)\right)$.

Suggested 2022-02-09 by Mark Ashbaugh

See also:

Annotations for §14.8(ii), §14.8 and Ch.14

►

14.8.10 $${𝑸}_{-n}\left(x\right)\to {(-1)}^{n+1}(n-1)!,$$ $n=1,2,3,\mathrm{\dots }$,

ⓘ

Symbols:

$!$: factorial (as in $n!$), ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable and $n$: nonnegative integer

Referenced by:

§14.8(ii)

Permalink:

http://dlmf.nist.gov/14.8.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(ii), §14.8 and Ch.14

►

14.8.11 $${𝑸}_{\nu }^{\mu }\left(x\right)\sim \frac{\mathrm{\Gamma }\left(\mu \right)}{2\mathrm{\Gamma }\left(\nu +\mu +1\right)}{\left(\frac{2}{x-1}\right)}^{\mu /2},$$ $\mathrm{\Re }\mu >0$, $\nu +\mu \ne -1,-2,-3,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\sim$: asymptotic equality, $\mathrm{\Re }$: real part, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.24

Permalink:

http://dlmf.nist.gov/14.8.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(ii), §14.8 and Ch.14

… ►

14.8.15 $${𝑸}_{\nu }^{\mu }\left(x\right)\sim \frac{{\pi }^{1/2}}{\mathrm{\Gamma }\left(\nu +\frac{3}{2}\right){(2x)}^{\nu +1}},$$ $\nu \ne -\frac{3}{2},-\frac{5}{2},-\frac{7}{2},\mathrm{\dots }$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.8(iii)

Permalink:

http://dlmf.nist.gov/14.8.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(iii), §14.8 and Ch.14

►

14.8.16 $${𝑸}_{-n-(1/2)}^{\mu }\left(x\right)\sim \frac{{\pi }^{1/2}\mathrm{\Gamma }\left(\mu +n+\frac{1}{2}\right)}{n!\mathrm{\Gamma }\left(\mu -n+\frac{1}{2}\right){(2x)}^{n+(1/2)}},$$ $n=1,2,3,\mathrm{\dots }$, $\mu -n+\frac{1}{2}\ne 0,-1,-2,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!$: factorial (as in $n!$), $x$: real variable, $n$: nonnegative integer and $\mu$: general order

Referenced by:

§14.21(iii), §14.8(iii)

Permalink:

http://dlmf.nist.gov/14.8.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(iii), §14.8 and Ch.14