金肯职业技术学院毕业证制作【言正 微aptao168】0oB4ifw
(0.004 seconds)
21—30 of 697 matching pages
21: 31.5 Solutions Analytic at Three Singularities: Heun Polynomials
22: 10.75 Tables
Achenbach (1986) tabulates , , , , , 20D or 18–20S.
Abramowitz and Stegun (1964, Chapter 11) tabulates , , , 10D; , , , 8D.
Zhang and Jin (1996, p. 270) tabulates , , , , , 8D.
Achenbach (1986) tabulates , , , , , 19D or 19–21S.
Abramowitz and Stegun (1964, Chapter 11) tabulates , , , 7D; , , , 6D.
23: 8.26 Tables
Pagurova (1963) tabulates and (with different notation) for , to 7D.
Pearson (1965) tabulates the function () for , to 7D, where rounds off to 1 to 7D; also for , to 5D.
Zhang and Jin (1996, Table 3.8) tabulates for , to 8D or 8S.
Abramowitz and Stegun (1964, pp. 245–248) tabulates for , to 7D; also for , to 6S.
Pagurova (1961) tabulates for , to 4-9S; for , to 7D; for , to 7S or 7D.
24: 22.5 Special Values
§22.5(ii) Limiting Values of
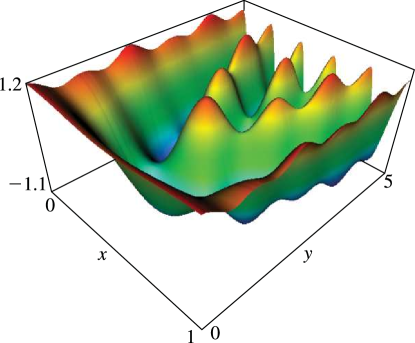
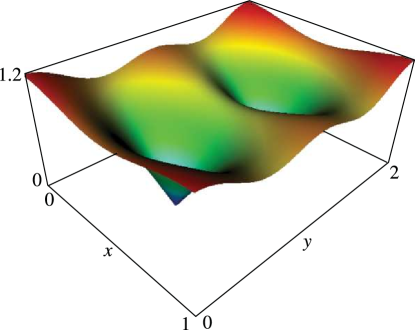
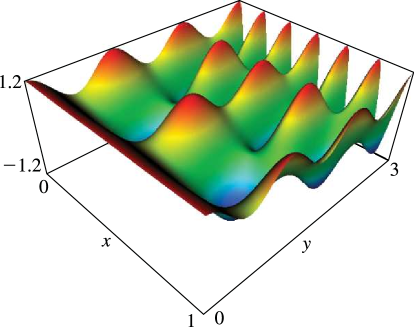
►If , then and ; if , then and . … ►Expansions for as or are given in §§19.5, 19.12. … ►25: 21.4 Graphics
26: 10.48 Graphs
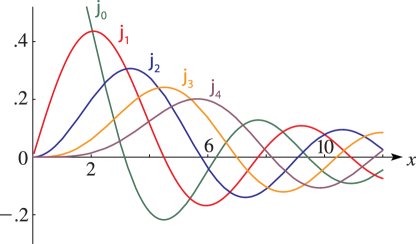 ►
►
 ►
►
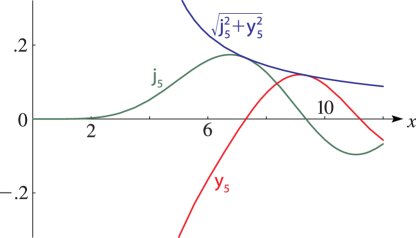 ►
►
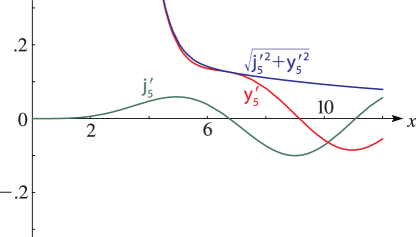 ►
►
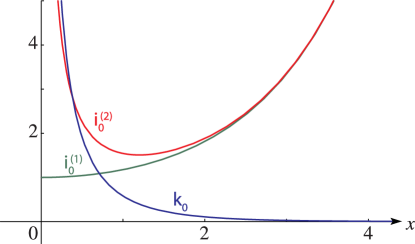 ►
►
27: 17.5 Functions
28: 36.15 Methods of Computation
29: 19.22 Quadratic Transformations
30: 7.23 Tables
Abramowitz and Stegun (1964, Chapter 7) includes , , , 10D; , , 8S; , , 7D; , , , 6S; , , 10D; , , 9D; , , , 7D; , , , , 15D.
Abramowitz and Stegun (1964, Table 27.6) includes the Goodwin–Staton integral , , 4D; also , , 4D.
Finn and Mugglestone (1965) includes the Voigt function , , , 6S.
Zhang and Jin (1996, pp. 637, 639) includes , , , 8D; , , , 8D.
Abramowitz and Stegun (1964, Chapter 7) includes , , , 6D.