推排九扑克牌咋玩【杏彩体育qee9.com】3cN

(0.002 seconds)

21—30 of 579 matching pages

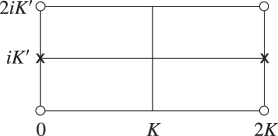
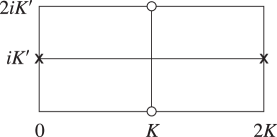
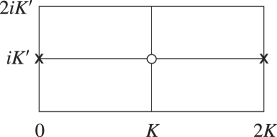
21: 22.17 Moduli Outside the Interval [0,1]

… ►

22.17.3

\operatorname{cn}\left(z,1/k\right)=\operatorname{dn}\left(z/k,k\right),

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $z$ : complex and $k$ : modulus
A&S Ref:: 16.11.3
Permalink:: http://dlmf.nist.gov/22.17.E3
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

►

22.17.4

\operatorname{dn}\left(z,1/k\right)=\operatorname{cn}\left(z/k,k\right).

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{dn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $z$ : complex and $k$ : modulus
A&S Ref:: 16.11.4
Permalink:: http://dlmf.nist.gov/22.17.E4
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

… ►

22.17.7

\operatorname{cn}\left(z,ik\right)=\operatorname{cd}\left(z/k_{1}^{\prime},k_{% 1}\right),

ⓘ

Symbols:: $\operatorname{cd}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $\mathrm{i}$ : imaginary unit, $z$ : complex, $k$ : modulus, $k_{1}$ : change of variable and $k_{1}^{\prime}$ : change of variable
A&S Ref:: 16.10.3 (modified)
Permalink:: http://dlmf.nist.gov/22.17.E7
Encodings:: pMML, png, TeX
See also:: Annotations for §22.17(i), §22.17 and Ch.22

…

22: 22.1 Special Notation

… ►The functions treated in this chapter are the three principal Jacobian elliptic functions

\operatorname{sn}\left(z,k\right)

\operatorname{cn}\left(z,k\right)

\operatorname{dn}\left(z,k\right)

; the nine subsidiary Jacobian elliptic functions

\operatorname{cd}\left(z,k\right)

\operatorname{sd}\left(z,k\right)

\operatorname{nd}\left(z,k\right)

\operatorname{dc}\left(z,k\right)

\operatorname{nc}\left(z,k\right)

\operatorname{sc}\left(z,k\right)

\operatorname{ns}\left(z,k\right)

\operatorname{ds}\left(z,k\right)

\operatorname{cs}\left(z,k\right)

; the amplitude function

\operatorname{am}\left(x,k\right)

; Jacobi’s epsilon and zeta functions

\mathcal{E}\left(x,k\right)

and

\mathrm{Z}\left(x|k\right)

. … ►The notation

\operatorname{sn}\left(z,k\right)

\operatorname{cn}\left(z,k\right)

\operatorname{dn}\left(z,k\right)

is due to Gudermann (1838), following Jacobi (1827); that for the subsidiary functions is due to Glaisher (1882). Other notations for

\operatorname{sn}\left(z,k\right)

are

\mathrm{sn}(z\mathpunct{|}m)

and

\mathrm{sn}(z,m)

with

m=k^{2}

; see Abramowitz and Stegun (1964) and Walker (1996). …

23: 22.15 Inverse Functions

… ►

22.15.2

\operatorname{cn}\left(\eta,k\right)=x,

-1\leq x\leq 1

ⓘ

Symbols:: $\operatorname{cn}\left(\NVar{z},\NVar{k}\right)$ : Jacobian elliptic function, $x$ : real, $k$ : modulus and $\eta$ : solution
Referenced by:: §22.15(i)
Permalink:: http://dlmf.nist.gov/22.15.E2
Encodings:: pMML, png, TeX
See also:: Annotations for §22.15(i), §22.15 and Ch.22

… ►are denoted respectively by … ►

\eta=\operatorname{arccn}\left(x,k\right),

… ►

22.15.6

0\leq\operatorname{arccn}\left(x,k\right)\leq 2K,

ⓘ

Symbols:: $K\left(\NVar{k}\right)$ : Legendre’s complete elliptic integral of the first kind, $\operatorname{arccn}\left(\NVar{x},\NVar{k}\right)$ : inverse Jacobian elliptic function, $x$ : real and $k$ : modulus
Permalink:: http://dlmf.nist.gov/22.15.E6
Encodings:: pMML, png, TeX
See also:: Annotations for §22.15(i), §22.15 and Ch.22

… ►

22.15.9

\eta=\pm\operatorname{arccn}\left(x,k\right)+4mK,

ⓘ

Symbols:: $K\left(\NVar{k}\right)$ : Legendre’s complete elliptic integral of the first kind, $\operatorname{arccn}\left(\NVar{x},\NVar{k}\right)$ : inverse Jacobian elliptic function, $x$ : real, $k$ : modulus, $\eta$ : solution and $m$ : integer
Permalink:: http://dlmf.nist.gov/22.15.E9
Encodings:: pMML, png, TeX
See also:: Annotations for §22.15(i), §22.15 and Ch.22

…

24: 22.4 Periods, Poles, and Zeros

… ►

Table 22.4.1: Periods and poles of Jacobian elliptic functions.

► ►►►

Periods	$z$ -Poles
Periods	…
$4K$ , $2K+2iK^{\prime}$	$\operatorname{cn}$	$\operatorname{sd}$	$\operatorname{nc}$	$\operatorname{ds}$
…

► … ►

Table 22.4.2: Periods and zeros of Jacobian elliptic functions.

► ►►►

Periods	$z$ -Zeros
Periods	…
$4K$ , $2K+2iK^{\prime}$	$\operatorname{sd}$	$\operatorname{cn}$	$\operatorname{ds}$	$\operatorname{nc}$
…

► … ►

See accompanying text — Figure 22.4.1: $z$ -plane. … Magnify

… ►

Table 22.4.3: Half- or quarter-period shifts of variable for the Jacobian elliptic functions.

► ►►►►

	$u$
…
$\operatorname{cn}u$	$-k^{\prime}\operatorname{sd}z$	$-ik^{\prime}k^{-1}\operatorname{nc}z$	$-ik^{-1}\operatorname{ds}z$	$-\operatorname{cn}z$	$\operatorname{cn}z$	$-\operatorname{cn}z$
…
$\operatorname{ds}u$	$k^{\prime}\operatorname{nc}z$	$ikk^{\prime}\operatorname{sd}z$	$-ik\operatorname{cn}z$	$-\operatorname{ds}z$	$\operatorname{ds}z$	$-\operatorname{ds}z$
…

►

25: 23.6 Relations to Other Functions

… ►In this subsection

2\omega_{1}

2\omega_{3}

are any pair of generators of the lattice

\mathbb{L}

, and the lattice roots

e_{1}

e_{2}

e_{3}

are given by (23.3.9). … ►Again, in Equations (23.6.16)–(23.6.26),

2\omega_{1},2\omega_{3}

are any pair of generators of the lattice

\mathbb{L}

and

e_{1},e_{2},e_{3}

are given by (23.3.9). … ►For representations of the Jacobi functions

\operatorname{sn}

\operatorname{cn}

, and

\operatorname{dn}

as quotients of

\sigma

-functions see Lawden (1989, §§6.2, 6.3). … ►Let

z

be on the perimeter of the rectangle with vertices

0,2\omega_{1},2\omega_{1}+2\omega_{3},2\omega_{3}

. … ►Let

z

be a point of

\mathbb{C}

different from

e_{1},e_{2},e_{3}

, and define

w

by …

26: 34.11 Higher-Order $3nj$ Symbols

§34.11 Higher-Order $3nj$ Symbols

…

27: 19.25 Relations to Other Functions

… ►where we assume

0\leq x^{2}\leq 1

x=\operatorname{sn}

\operatorname{cn}

, or

\operatorname{cd}

;

x^{2}\geq 1

x=\operatorname{ns}

\operatorname{nc}

, or

\operatorname{dc}

;

x

real if

x=\operatorname{cs}

\operatorname{sc}

;

k^{\prime}\leq x\leq 1

x=\operatorname{dn}

;

1\leq x\leq 1/k^{\prime}

x=\operatorname{nd}

;

x^{2}\geq{k^{\prime}}^{2}

x=\operatorname{ds}

;

0\leq x^{2}\leq 1/{k^{\prime}}^{2}

x=\operatorname{sd}

. … ►In (19.25.38) and (19.25.39)

j

k

\ell

is any permutation of the numbers

1,2,3

. … ►in which

2\omega_{1}

and

2\omega_{3}

are generators for the lattice

\mathbb{L}

\omega_{2}=-\omega_{1}-\omega_{3}

, and

\eta_{j}=\zeta\left(\omega_{j}\right)

(see (23.2.12)). … ►(

{F_{1}}

and

F_{D}

are equivalent to the

R

-function of 3 and

n

variables, respectively, but lack full symmetry.) …

28: 4.17 Special Values and Limits

… ►

Table 4.17.1: Trigonometric functions: values at multiples of

\frac{1}{12}\pi

► ►►►►►►►

$\theta$	$\sin\theta$	$\cos\theta$	$\tan\theta$	$\csc\theta$	$\sec\theta$	$\cot\theta$
…
$\pi/12$	$\frac{1}{4}\sqrt{2}(\sqrt{3}-1)$	$\frac{1}{4}\sqrt{2}(\sqrt{3}+1)$	$2-\sqrt{3}$	$\sqrt{2}(\sqrt{3}+1)$	$\sqrt{2}(\sqrt{3}-1)$	$2+\sqrt{3}$
$\pi/6$	$\frac{1}{2}$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{3}\sqrt{3}$	$2$	$\frac{2}{3}\sqrt{3}$	$\sqrt{3}$
…
$\pi/3$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{2}{3}\sqrt{3}$	$2$	$\frac{1}{3}\sqrt{3}$
…
$2\pi/3$	$\frac{1}{2}\sqrt{3}$	$-\frac{1}{2}$	$-\sqrt{3}$	$\frac{2}{3}\sqrt{3}$	$-2$	$-\frac{1}{3}\sqrt{3}$
…
$5\pi/6$	$\frac{1}{2}$	$-\frac{1}{2}\sqrt{3}$	$-\frac{1}{3}\sqrt{3}$	$2$	$-\frac{2}{3}\sqrt{3}$	$-\sqrt{3}$
…

► …

29: Errata

… ►

Equations (22.14.16), (22.14.17)

22.14.16

\int_{0}^{K\left(k\right)}\ln\left(\operatorname{sn}\left(t,k\right)\right)\,% \mathrm{d}t=-\tfrac{\pi}{4}{K^{\prime}}\left(k\right)-\tfrac{1}{2}K\left(k% \right)\ln k,

22.14.17

\int_{0}^{K\left(k\right)}\ln\left(\operatorname{cn}\left(t,k\right)\right)\,% \mathrm{d}t=-\tfrac{\pi}{4}{K^{\prime}}\left(k\right)+\tfrac{1}{2}K\left(k% \right)\ln\left(k^{\prime}/k\right)

Originally, a factor of $\pi$ was missing from the terms containing the $-\tfrac{1}{4}{K^{\prime}}\left(k\right)$ .

Reported by Fred Hucht on 2020-08-06

… ►

Equations (22.9.8), (22.9.9) and (22.9.10)

22.9.8

s_{1,3}^{(4)}s_{2,3}^{(4)}+s_{2,3}^{(4)}s_{3,3}^{(4)}+s_{3,3}^{(4)}s_{1,3}^{(4% )}=\frac{\kappa^{2}-1}{k^{2}}

22.9.9

c_{1,3}^{(4)}c_{2,3}^{(4)}+c_{2,3}^{(4)}c_{3,3}^{(4)}+c_{3,3}^{(4)}c_{1,3}^{(4% )}=-\frac{\kappa(\kappa+2)}{(1+\kappa)^{2}}

22.9.10

d_{1,3}^{(2)}d_{2,3}^{(2)}+d_{2,3}^{(2)}d_{3,3}^{(2)}+d_{3,3}^{(2)}d_{1,3}^{(2% )}=d_{1,3}^{(4)}d_{2,3}^{(4)}+d_{2,3}^{(4)}d_{3,3}^{(4)}+d_{3,3}^{(4)}d_{1,3}^% {(4)}=\kappa(\kappa+2)

Originally all the functions $s_{m,p}^{(4)}$ , $c_{m,p}^{(4)}$ , $d_{m,p}^{(2)}$ and $d_{m,p}^{(4)}$ in Equations (22.9.8), (22.9.9) and (22.9.10) were written incorrectly with $p=2$ . These functions have been corrected so that they are written with $p=3$ . In the sentence just below (22.9.10), the expression $s_{m,2}^{(4)}s_{n,2}^{(4)}$ has been corrected to read $s_{m,p}^{(4)}s_{n,p}^{(4)}$ .

Reported by Juan Miguel Nieto on 2019-11-07

… ►

Equation (22.19.6)

22.19.6

x(t)=\operatorname{cn}\left(t\sqrt{1+2\eta},k\right)

Originally the term $\sqrt{1+2\eta}$ was given incorrectly as $\sqrt{1+\eta}$ in this equation and in the line above. Additionally, for improved clarity, the modulus $k=1/\sqrt{2+\eta^{-1}}$ has been defined in the line above.

Reported 2014-05-02 by Svante Janson.

… ►

Equation (34.3.7)

34.3.7

\begin{pmatrix}j_{1}&j_{2}&j_{3}\\ j_{1}&-j_{1}-m_{3}&m_{3}\end{pmatrix}=(-1)^{j_{1}-j_{2}-m_{3}}\left(\frac{(2j_% {1})!(-j_{1}+j_{2}+j_{3})!(j_{1}+j_{2}+m_{3})!(j_{3}-m_{3})!}{(j_{1}+j_{2}+j_{% 3}+1)!(j_{1}-j_{2}+j_{3})!(j_{1}+j_{2}-j_{3})!(-j_{1}+j_{2}-m_{3})!(j_{3}+m_{3% })!}\right)^{\frac{1}{2}}

In the original equation the prefactor of the above 3j symbol read $(-1)^{-j_{2}+j_{3}+m_{3}}$ . It is now replaced by its correct value $(-1)^{j_{1}-j_{2}-m_{3}}$ .

Reported 2014-06-12 by James Zibin.

… ►

Equation (22.6.7)

22.6.7

\operatorname{dn}\left(2z,k\right)=\frac{{\operatorname{dn}}^{2}\left(z,k% \right)-k^{2}{\operatorname{sn}}^{2}\left(z,k\right){\operatorname{cn}}^{2}% \left(z,k\right)}{1-k^{2}{\operatorname{sn}}^{4}\left(z,k\right)}=\frac{{% \operatorname{dn}}^{4}\left(z,k\right)+k^{2}{k^{\prime}}^{2}{\operatorname{sn}% }^{4}\left(z,k\right)}{1-k^{2}{\operatorname{sn}}^{4}\left(z,k\right)}

Originally the term $k^{2}{\operatorname{sn}}^{2}\left(z,k\right){\operatorname{cn}}^{2}\left(z,k\right)$ was given incorrectly as $k^{2}{\operatorname{sn}}^{2}\left(z,k\right){\operatorname{dn}}^{2}\left(z,k\right)$ .

Reported 2014-02-28 by Svante Janson.

…

30: 29.17 Other Solutions

… ►They are algebraic functions of

\operatorname{sn}\left(z,k\right)

\operatorname{cn}\left(z,k\right)

, and

\operatorname{dn}\left(z,k\right)

, and have primitive period

8K

. …


(a) $\operatorname{sn}\left(z,k\right)$	(b) $\operatorname{cn}\left(z,k\right)$	(c) $\operatorname{dn}\left(z,k\right)$

推排九扑克牌咋玩【杏彩体育qee9.com】3cN

21—30 of 579 matching pages

21: 22.17 Moduli Outside the Interval [0,1]

22: 22.1 Special Notation

23: 22.15 Inverse Functions

24: 22.4 Periods, Poles, and Zeros

25: 23.6 Relations to Other Functions

26: 34.11 Higher-Order 3 ⁢ n ⁢ j Symbols

§34.11 Higher-Order 3 ⁢ n ⁢ j Symbols

27: 19.25 Relations to Other Functions

28: 4.17 Special Values and Limits

29: Errata

30: 29.17 Other Solutions

26: 34.11 Higher-Order $3nj$ Symbols

§34.11 Higher-Order $3nj$ Symbols