contour
(0.001 seconds)
11—20 of 56 matching pages
11: 31.10 Integral Equations and Representations
…
►for a suitable contour
.
…The contour
must be such that
…
►Here is a normalization constant and is the contour of Example 1.
…
►for suitable contours
, .
…The contours
, must be chosen so that
…
12: 36.3 Visualizations of Canonical Integrals
…
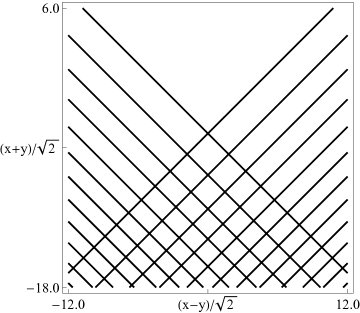
►In Figure 36.3.13(a) points of confluence of phase contours are zeros of ; similarly for other contour plots in this subsection.
…
►
►
►
►
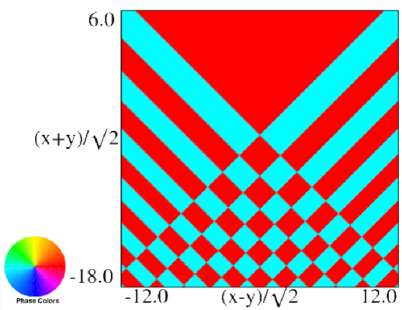
Figure 36.3.15: Phase of elliptic umbilic canonical integral .
…
Magnify
►
 |
 |
| (a) Contour plot. | (b) Density plot. |
►
►
►
Figure 36.3.16: Phase of elliptic umbilic canonical integral .
…
Magnify
►
 |
 |
| (a) Contour plot. | (b) Density plot. |
►
►
►
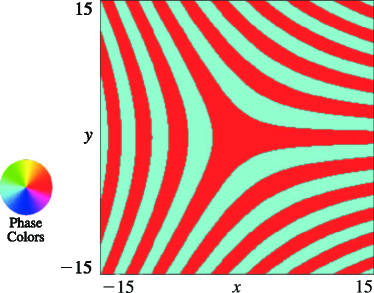
Figure 36.3.17: Phase of elliptic umbilic canonical integral .
…
Magnify
►
…
 |
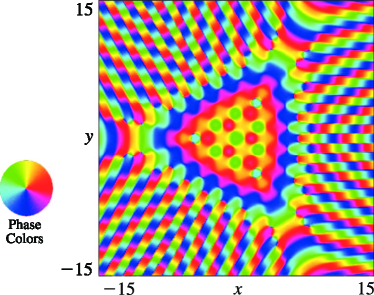 |
| (a) Contour plot. | (b) Density plot. |
13: 1.9 Calculus of a Complex Variable
…
►
§1.9(iii) Integration
… ►A simple closed contour is a simple contour, except that . … ►If is continuous within and on a simple closed contour and analytic within , then … ►Winding Number
…14: 1.10 Functions of a Complex Variable
…
►Let be a simple closed contour consisting of a segment of the real axis and a contour in the upper half-plane joining the ends of .
…
►and the integration contour is described once in the positive sense.
…
►Each contour is called a cut.
…(Or more generally, a simple contour that starts at the center and terminates on the boundary.)
…
►
§1.10(viii) Functions Defined by Contour Integrals
…15: 18.10 Integral Representations
…
►
§18.10(iii) Contour Integral Representations
►Table 18.10.1 gives contour integral representations of the form ►
18.10.8
…
►Here is a simple closed contour encircling once in the positive sense.
►
…
16: 31.6 Path-Multiplicative Solutions
…
►This denotes a set of solutions of (31.2.1) with the property that if we pass around a simple closed contour in the -plane that encircles and once in the positive sense, but not the remaining finite singularity, then the solution is multiplied by a constant factor .
…
17: 31.9 Orthogonality
…
►
31.9.2
…
►The integration path is called a Pochhammer double-loop
contour (compare Figure 5.12.3).
…
►and the integration paths , are Pochhammer double-loop contours encircling distinct pairs of singularities , , .
…
18: 2.4 Contour Integrals
§2.4 Contour Integrals
… ►The most successful results are obtained on moving the integration contour as far to the left as possible. … ►Let denote the path for the contour integral ►
2.4.10
…
►and assigning an appropriate value to to modify the contour, the approximating integral is reducible to an Airy function or a Scorer function (§§9.2, 9.12).
…
19: 13.16 Integral Representations
…
►