associated Legendre functions

SearchAdvancedHelp

(0.011 seconds)

11—20 of 66 matching pages

11: 14.32 Methods of Computation

§14.32 Methods of Computation

…

12: 14.5 Special Values

… ►

14.5.9 $${𝑸}_0\left(x\right)=\frac{1}{2}\ln \left(\frac{x+1}{x-1}\right),$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function and $x$: real variable

A&S Ref:

8.4.2 (modified)

Permalink:

http://dlmf.nist.gov/14.5.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §14.5(ii), §14.5 and Ch.14

►

14.5.10 $${𝑸}_1\left(x\right)=\frac{x}{2}\ln \left(\frac{x+1}{x-1}\right)-1.$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function and $x$: real variable

A&S Ref:

8.4.4 (modified)

Permalink:

http://dlmf.nist.gov/14.5.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §14.5(ii), §14.5 and Ch.14

… ►

§14.5(v) $\mu =0$, $\nu =\pm \frac{1}{2}$

… ► … ►

14.5.30 $${𝑸}_2\left(x\right)=\frac{3x^2-1}{8}\ln \left(\frac{x+1}{x-1}\right)-\frac{3}{4}x.$$

ⓘ

Symbols:

$\ln z$: principal branch of logarithm function, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function and $x$: real variable

Referenced by:

(14.5.30)

Permalink:

http://dlmf.nist.gov/14.5.E30

Encodings:

pMML, png, TeX

Addition (effective with 1.0.7):

(14.5.30) has been added to this section.

See also:

Annotations for §14.5(vi), §14.5 and Ch.14

13: 14.7 Integer Degree and Order

§14.7 Integer Degree and Order

►

§14.7(i) $\mu =0$

… ►

§14.7(ii) Rodrigues-Type Formulas

… ►

§14.7(iv) Generating Functions

… ►

14: 14.4 Graphics

… ►

§14.4(iii) Associated Legendre Functions: 2D Graphs

… ►

§14.4(iv) Associated Legendre Functions: 3D Surfaces

… ►

►

►

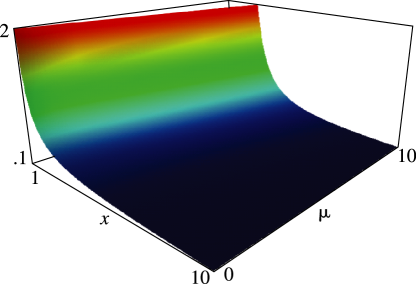
Figure 14.4.32: ${𝑸}_0^{\mu }\left(x\right)$, $0\le \mu \le 10$, . Magnify 3D Help

15: 14.8 Behavior at Singularities

… ► … ►

14.8.9 $${𝑸}_{\nu }\left(x\right)=-\frac{\ln \left(x-1\right)}{2\mathrm{\Gamma }\left(\nu +1\right)}+\frac{\frac{1}{2}\ln 2-\gamma -\psi \left(\nu +1\right)}{\mathrm{\Gamma }\left(\nu +1\right)}+O\left(\left(x-1\right)\ln \left(x-1\right)\right),$$ $\nu \ne -1,-2,-3,\mathrm{\dots }$,

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{\Gamma }\left(z\right)$: gamma function, $\gamma$: Euler’s constant, $\psi \left(z\right)$: psi (or digamma) function, $\ln z$: principal branch of logarithm function, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable and $\nu$: general degree

Referenced by:

Erratum (V1.1.5) for Equation (14.8.9)

Permalink:

http://dlmf.nist.gov/14.8.E9

Encodings:

pMML, png, TeX

Correction (effective with 1.1.5):

The symbol $O\left(x-1\right)$ has been corrected to be $O\left(\left(x-1\right)\ln \left(x-1\right)\right)$.

Suggested 2022-02-09 by Mark Ashbaugh

See also:

Annotations for §14.8(ii), §14.8 and Ch.14

… ►

14.8.11 $${𝑸}_{\nu }^{\mu }\left(x\right)\sim \frac{\mathrm{\Gamma }\left(\mu \right)}{2\mathrm{\Gamma }\left(\nu +\mu +1\right)}{\left(\frac{2}{x-1}\right)}^{\mu /2},$$ $\mathrm{\Re }\mu >0$, $\nu +\mu \ne -1,-2,-3,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\sim$: asymptotic equality, $\mathrm{\Re }$: real part, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.24

Permalink:

http://dlmf.nist.gov/14.8.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(ii), §14.8 and Ch.14

… ►

14.8.15 $${𝑸}_{\nu }^{\mu }\left(x\right)\sim \frac{{\pi }^{1/2}}{\mathrm{\Gamma }\left(\nu +\frac{3}{2}\right){(2x)}^{\nu +1}},$$ $\nu \ne -\frac{3}{2},-\frac{5}{2},-\frac{7}{2},\mathrm{\dots }$,

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.8(iii)

Permalink:

http://dlmf.nist.gov/14.8.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(iii), §14.8 and Ch.14

►

14.8.16 $${𝑸}_{-n-(1/2)}^{\mu }\left(x\right)\sim \frac{{\pi }^{1/2}\mathrm{\Gamma }\left(\mu +n+\frac{1}{2}\right)}{n!\mathrm{\Gamma }\left(\mu -n+\frac{1}{2}\right){(2x)}^{n+(1/2)}},$$ $n=1,2,3,\mathrm{\dots }$, $\mu -n+\frac{1}{2}\ne 0,-1,-2,\mathrm{\dots }$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!$: factorial (as in $n!$), $x$: real variable, $n$: nonnegative integer and $\mu$: general order

Referenced by:

§14.21(iii), §14.8(iii)

Permalink:

http://dlmf.nist.gov/14.8.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §14.8(iii), §14.8 and Ch.14

16: 14.24 Analytic Continuation

§14.24 Analytic Continuation

… ►

14.24.1 $$P_{\nu }^{-\mu }\left(z{\mathrm{e}}^{s\pi \mathrm{i}}\right)={\mathrm{e}}^{s\nu \pi \mathrm{i}}{P}_{\nu }^{-\mu }\left(z\right)+\frac{2\mathrm{i}\sin \left(\left(\nu +\frac{1}{2}\right)s\pi \right){\mathrm{e}}^{-s\pi \mathrm{i}/2}}{\cos \left(\nu \pi \right)\mathrm{\Gamma }\left(\mu -\nu \right)}{𝑸}_{\nu }^{\mu }\left(z\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $z$: complex variable, $\mu$: general order, $\nu$: general degree and $s$: arbitrary integer

Referenced by:

§14.24, §14.24

Permalink:

http://dlmf.nist.gov/14.24.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §14.24 and Ch.14

►

14.24.2 $${𝑸}_{\nu }^{\mu }\left(z{\mathrm{e}}^{s\pi \mathrm{i}}\right)={(-1)}^s{\mathrm{e}}^{-s\nu \pi \mathrm{i}}{𝑸}_{\nu }^{\mu }\left(z\right),$$

ⓘ

Symbols:

${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable, $\mu$: general order, $\nu$: general degree and $s$: arbitrary integer

Referenced by:

§14.23, §14.24

Permalink:

http://dlmf.nist.gov/14.24.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §14.24 and Ch.14

… ►

14.24.4 $${𝑸}_{\nu ,s}^{\mu }\left(z\right)={\mathrm{e}}^{-s\mu \pi \mathrm{i}}{𝑸}_{\nu }^{\mu }\left(z\right)-\frac{\pi \mathrm{i}\sin \left(s\mu \pi \right)}{\sin \left(\mu \pi \right)\mathrm{\Gamma }\left(\nu -\mu +1\right)}{P}_{\nu }^{-\mu }\left(z\right),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $z$: complex variable, $\mu$: general order, $\nu$: general degree and $s$: arbitrary integer

Referenced by:

§14.24

Permalink:

http://dlmf.nist.gov/14.24.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §14.24 and Ch.14

… ►For fixed $z$, other than $\pm 1$ or $\mathrm{\infty }$, each branch of $P_{\nu }^{-\mu }\left(z\right)$ and ${𝑸}_{\nu }^{\mu }\left(z\right)$ is an entire function of each parameter $\nu$ and $\mu$. …

17: 14.10 Recurrence Relations and Derivatives

§14.10 Recurrence Relations and Derivatives

… ►

14.10.6 $$P_{\nu }^{\mu +2}\left(x\right)+2(\mu +1)x{\left(x^2-1\right)}^{-1/2}{P}_{\nu }^{\mu +1}\left(x\right)-(\nu -\mu )(\nu +\mu +1)P_{\nu }^{\mu }\left(x\right)=0,$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.10, §14.14

Permalink:

http://dlmf.nist.gov/14.10.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

►

14.10.7 $${\left(x^2-1\right)}^{1/2}{P}_{\nu }^{\mu +1}\left(x\right)-(\nu -\mu +1)P_{\nu +1}^{\mu }\left(x\right)+(\nu +\mu +1)x{P}_{\nu }^{\mu }\left(x\right)=0.$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.10, §14.21(iii)

Permalink:

http://dlmf.nist.gov/14.10.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §14.10 and Ch.14

…

18: 14.6 Integer Order

§14.6 Integer Order

… ►

14.6.3 $$P_{\nu }^m\left(x\right)={\left(x^2-1\right)}^{m/2}\frac{d^m{P}_{\nu }\left(x\right)}{{dx}^m},$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $P_{\nu }\left(z\right)=P_{\nu }^0\left(z\right)$: Legendre function of the first kind, $x$: real variable, $m$: nonnegative integer and $\nu$: general degree

A&S Ref:

8.6.6

Referenced by:

§14.21(iii)

Permalink:

http://dlmf.nist.gov/14.6.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §14.6(i), §14.6 and Ch.14

►

14.6.4 $$Q_{\nu }^m\left(x\right)={\left(x^2-1\right)}^{m/2}\frac{d^m{Q}_{\nu }\left(x\right)}{{dx}^m},$$

ⓘ

Symbols:

$Q_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the second kind, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $Q_{\nu }\left(z\right)=Q_{\nu }^0\left(z\right)$: Legendre function of the second kind, $x$: real variable, $m$: nonnegative integer and $\nu$: general degree

A&S Ref:

8.6.7

Referenced by:

§14.6(i)

Permalink:

http://dlmf.nist.gov/14.6.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §14.6(i), §14.6 and Ch.14

►

14.6.5 $${\left(\nu +1\right)}_m{𝑸}_{\nu }^m\left(x\right)={(-1)}^m{\left(x^2-1\right)}^{m/2}\frac{d^m{𝑸}_{\nu }\left(x\right)}{{dx}^m}.$$

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable, $m$: nonnegative integer and $\nu$: general degree

Referenced by:

§14.21(iii), §14.6(i)

Permalink:

http://dlmf.nist.gov/14.6.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §14.6(i), §14.6 and Ch.14

… ►

19: 14.12 Integral Representations

… ►

§14.12(ii)

… ►

14.12.5 $$P_{\nu }^{-\mu }\left(x\right)=\frac{{\left(x^2-1\right)}^{-\mu /2}}{\mathrm{\Gamma }\left(\mu \right)}{\int }_1^x{P}_{\nu }\left(t\right){(x-t)}^{\mu -1}dt,$$ $\mathrm{\Re }\mu >0$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $P_n\left(x\right)$: Legendre polynomial, $dx$: differential of $x$ , $\int$: integral, $\mathrm{\Re }$: real part, $x$: real variable, $\mu$: general order and $\nu$: general degree

Referenced by:

§14.17(i)

Permalink:

http://dlmf.nist.gov/14.12.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12 and Ch.14

►

14.12.6 $${𝑸}_{\nu }^{\mu }\left(x\right)=\frac{{\pi }^{1/2}{\left(x^2-1\right)}^{\mu /2}}{2^{\mu }\mathrm{\Gamma }\left(\mu +\frac{1}{2}\right)\mathrm{\Gamma }\left(\nu -\mu +1\right)}{\int }_0^{\mathrm{\infty }}\frac{{(\sinh t)}^{2\mu }}{{\left(x+{(x^2-1)}^{1/2}\cosh t\right)}^{\nu +\mu +1}}dt,$$ $\mathrm{\Re }\left(\nu +1\right)>\mathrm{\Re }\mu >-\frac{1}{2}$.

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\int$: integral, $\mathrm{\Re }$: real part, $x$: real variable, $\mu$: general order and $\nu$: general degree

A&S Ref:

8.8.2 (modified)

Permalink:

http://dlmf.nist.gov/14.12.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12 and Ch.14

… ►

14.12.12 $${𝑸}_n^m\left(x\right)=\frac{1}{(n-m)!}{P}_n^m\left(x\right){\int }_x^{\mathrm{\infty }}\frac{dt}{\left(t^2-1\right){\left(P_n^m\left(t\right)\right)}^2},$$ $n\ge m$.

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, ${𝑸}_{\nu }^{\mu }\left(z\right)$: Olver’s associated Legendre function, $dx$: differential of $x$ , $!$: factorial (as in $n!$), $\int$: integral, $x$: real variable, $m$: nonnegative integer and $n$: nonnegative integer

Referenced by:

§14.17(i)

Permalink:

http://dlmf.nist.gov/14.12.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12 and Ch.14

… ►

14.12.14 $${𝑸}_n\left(x\right)=\frac{1}{n!}{\int }_0^{\mathrm{\infty }}\frac{dt}{{\left(x+{(x^2-1)}^{1/2}\cosh t\right)}^{n+1}}.$$

ⓘ

Symbols:

$dx$: differential of $x$ , $!$: factorial (as in $n!$), $\cosh z$: hyperbolic cosine function, $\int$: integral, ${𝑸}_{\nu }\left(z\right)={𝑸}_{\nu }^0\left(z\right)$: Olver’s associated Legendre function, $x$: real variable and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/14.12.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §14.12(ii), §14.12(ii), §14.12 and Ch.14

…

20: 14.14 Continued Fractions

§14.14 Continued Fractions

►

14.14.1 $$\frac{1}{2}{\left(x^2-1\right)}^{1/2}\frac{P_{\nu }^{\mu }\left(x\right)}{P_{\nu }^{\mu -1}\left(x\right)}=\frac{x_0}{y_0+}\frac{x_1}{y_1+}\frac{x_2}{y_2+}\mathrm{\cdots },$$

ⓘ

Symbols:

$P_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the first kind, $x$: real variable, $\mu$: general order, $\nu$: general degree, $x_k$: numerator and $x_k$: denominator

Referenced by:

§14.14

Permalink:

http://dlmf.nist.gov/14.14.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §14.14 and Ch.14

… ►

14.14.3 $$(\nu -\mu )\frac{Q_{\nu }^{\mu }\left(x\right)}{Q_{\nu -1}^{\mu }\left(x\right)}=\frac{x_0}{y_0-}\frac{x_1}{y_1-}\frac{x_2}{y_2-}\mathrm{\cdots },$$ $\nu \ne \mu$,

ⓘ

Symbols:

$Q_{\nu }^{\mu }\left(z\right)$: associated Legendre function of the second kind, $x$: real variable, $\mu$: general order, $\nu$: general degree, $x_k$: numerator and $x_k$: denominator

Referenced by:

§14.14

Permalink:

http://dlmf.nist.gov/14.14.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §14.14 and Ch.14

…