Jacobi identity

SearchAdvancedHelp

(0.002 seconds)

21—26 of 26 matching pages

21: Bibliography L

… ►

Lie algebraic approaches to classical partition identities. Adv. in Math. 29 (1), pp. 15–59.

ⓘ

External Links:

ISSN 0001-8708, Document, MathReview (S. I. Gel’fand), ZentralBlatt

Referenced by:

§17.16.

Encodings:

BibTeX

►

A Lie theoretic interpretation and proof of the Rogers-Ramanujan identities. Adv. in Math. 45 (1), pp. 21–72.

ⓘ

External Links:

ISSN 0001-8708, Document, MathReview (George E. Andrews), ZentralBlatt

Referenced by:

§17.16.

Encodings:

BibTeX

… ►

Co-recursive associated Jacobi polynomials. J. Comput. Appl. Math. 57 (1-2), pp. 203–213.

ⓘ

External Links:

ISSN 0377-0427, Document, MathReview, ZentralBlatt

Referenced by:

§18.30(i).

Encodings:

BibTeX

… ►

Jacobi polynomial expansions of a generalized hypergeometric function over a semi-infinite ray. Math. Comp. 17 (84), pp. 395–404.

ⓘ

External Links:

FullText, MathReview (I. A. Stegun), ZentralBlatt

Referenced by:

2nd item.

Encodings:

BibTeX

…

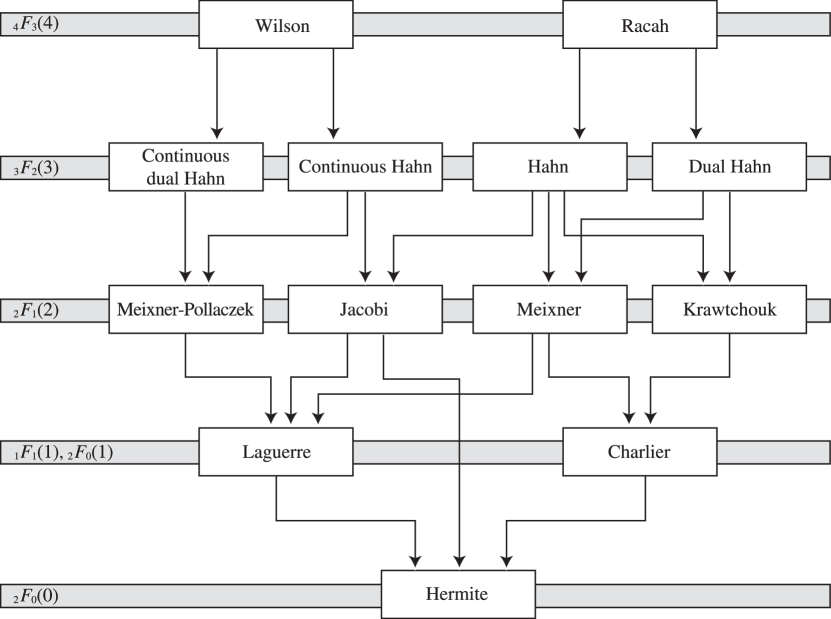
22: 18.21 Hahn Class: Interrelations

… ►

Hahn $\to$ Jacobi

►

18.21.5 $$\underset{N\to \mathrm{\infty }}{lim}{Q}_n(Nx;\alpha ,\beta ,N)=\frac{P_n^{(\alpha ,\beta )}\left(1-2x\right)}{P_n^{(\alpha ,\beta )}\left(1\right)}.$$

ⓘ

Symbols:

$Q_n(x;\alpha ,\beta ,N)$: Hahn polynomial, $P_n^{(\alpha ,\beta )}\left(x\right)$: Jacobi polynomial, $N$: positive integer, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.21(ii)

Permalink:

http://dlmf.nist.gov/18.21.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §18.21(ii), §18.21(ii), §18.21 and Ch.18

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

23: Bibliography M

… ►

An elementary proof of the Macdonald identities for $A_l^{(1)}$ . Adv. in Math. 57 (1), pp. 34–70.

ⓘ

External Links:

ISSN 0001-8708, Document, MathReview (Y. Lehrer-Ilamed), ZentralBlatt

Referenced by:

§17.15.

Encodings:

BibTeX

… ►

Infinite families of exact sums of squares formulas, Jacobi elliptic functions, continued fractions, and Schur functions. Ramanujan J. 6 (1), pp. 7–149.

ⓘ

External Links:

Document, ZentralBlatt

Referenced by:

§27.13(iv).

Encodings:

BibTeX

… ►

New infinite families of exact sums of squares formulas, Jacobi elliptic functions, and Ramanujan’s tau function. Proc. Nat. Acad. Sci. U.S.A. 93 (26), pp. 15004–15008.

ⓘ

External Links:

ISSN 0027-8424, MathReview (Ken Ono), ZentralBlatt

Referenced by:

§27.13(iv).

Encodings:

BibTeX

…

24: 17.8 Special Cases of ${}_r{}^{}\psi _r^{}$ Functions

… ►

Jacobi’s Triple Product

… ►

Quintuple Product Identity

…

25: 18.36 Miscellaneous Polynomials

… ►

§18.36(i) Jacobi-Type Polynomials

►These are OP’s on the interval $(-1,1)$ with respect to an orthogonality measure obtained by adding constant multiples of “Dirac delta weights” at $-1$ and $1$ to the weight function for the Jacobi polynomials. … ►The possibility of generalization to $\alpha =-k$, for $k\in \mathbb{N}$, is implicit in the identity Szegő (1975, page 102), … ►

18.36.7 $$T_k(y)\equiv -x{y}^{\prime \prime }+\frac{x-k}{x+k}((x+k+1)y^{\prime }-y)=(n-1)y.$$

ⓘ

Symbols:

$\equiv$: equals by definition, $y$: real variable, $k$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.36(vi)

Permalink:

http://dlmf.nist.gov/18.36.E7

Encodings:

pMML, png, TeX

Addition (effective with 1.2.0):

This equation was added.

See also:

Annotations for §18.36(vi), §18.36(vi), §18.36 and Ch.18

…

26: Bibliography W

… ►

An algorithmic proof theory for hypergeometric (ordinary and “$q$”) multisum/integral identities. Invent. Math. 108, pp. 575–633.

ⓘ

External Links:

ISSN 0020-9910, Document, MathReview (David R. Masson), ZentralBlatt

Referenced by:

§16.4(iii).

Encodings:

BibTeX

►

Rational function certification of multisum/integral/“$q$” identities. Bull. Amer. Math. Soc. (N.S.) 27 (1), pp. 148–153.

ⓘ

External Links:

ISSN 0273-0979, Pdf, Document, MathReview (Robert A. Gustafson), ZentralBlatt

Referenced by:

§16.4(iii).

Encodings:

BibTeX

… ►

Explicit formulas for the associated Jacobi polynomials and some applications. Canad. J. Math. 39 (4), pp. 983–1000.

ⓘ

External Links:

ISSN 0008-414X, MathReview (W. A. Al-Salam), ZentralBlatt

Referenced by:

§18.30(i), §18.30.

Encodings:

BibTeX

… ►

Asymptotic monotonicity of the relative extrema of Jacobi polynomials. Canad. J. Math. 46 (6), pp. 1318–1337.

ⓘ

External Links:

ISSN 0008-414X, MathReview (S. I. Drobnies), ZentralBlatt

Referenced by:

§18.14(iii).

Encodings:

BibTeX

… ►

Estimates for the error term in a uniform asymptotic expansion of the Jacobi polynomials. Anal. Appl. (Singap.) 1 (2), pp. 213–241.

ⓘ

External Links:

ISSN 0219-5305, Document, MathReview (Eberhard Wagner), ZentralBlatt

Referenced by:

§18.15(i), §18.15(i).

Encodings:

BibTeX

…