Hermite polynomials

SearchAdvancedHelp

(0.007 seconds)

11—20 of 59 matching pages

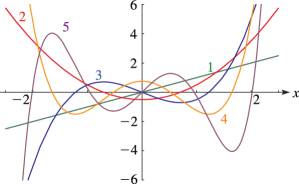
11: 18.4 Graphics

… ►

►►

Figure 18.4.7: Monic Hermite polynomials $h_n(x)=2^{-n}{H}_n\left(x\right)$, $n=1,2,3,4,5$. Magnify

…

12: 18.5 Explicit Representations

… ►

$H_0\left(x\right)=1,$

►

$H_1\left(x\right)=2x,$

►

$H_2\left(x\right)=4x^2-2,$

… ►

${\mathrm{𝐻𝑒}}_0\left(x\right)=1,$

►

${\mathrm{𝐻𝑒}}_1\left(x\right)=x,$

…

13: 18.11 Relations to Other Functions

… ►

Hermite

►

18.11.3 $$H_n\left(x\right)=2^{n}U(-\frac{1}{2}n,\frac{1}{2},x^2)=2^{n}xU(-\frac{1}{2}n+\frac{1}{2},\frac{3}{2},x^2)=2^{\frac{1}{2}n}{\mathrm{e}}^{\frac{1}{2}{x}^2}U(-n-\frac{1}{2},2^{\frac{1}{2}}x),$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, $U(a,b,z)$: Kummer confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $U(a,z)$: parabolic cylinder function, $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.5.55, 22.5.58 ((factor $x$ missing on RHS of 22.5.55))

Referenced by:

§18.11(i), §18.15(v)

Permalink:

http://dlmf.nist.gov/18.11.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §18.11(i), §18.11(i), §18.11 and Ch.18

►

18.11.4 $${\mathrm{𝐻𝑒}}_n\left(x\right)=2^{\frac{1}{2}n}U(-\frac{1}{2}n,\frac{1}{2},\frac{1}{2}{x}^2)=2^{\frac{1}{2}(n-1)}xU(-\frac{1}{2}n+\frac{1}{2},\frac{3}{2},\frac{1}{2}{x}^2)={\mathrm{e}}^{\frac{1}{4}{x}^2}U(-n-\frac{1}{2},x).$$

ⓘ

Symbols:

${\mathrm{𝐻𝑒}}_n\left(x\right)$: Hermite polynomial, $U(a,b,z)$: Kummer confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $U(a,z)$: parabolic cylinder function, $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.5.59

Permalink:

http://dlmf.nist.gov/18.11.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §18.11(i), §18.11(i), §18.11 and Ch.18

… ►

Hermite

►

18.11.7 $$\underset{n\to \mathrm{\infty }}{lim}\frac{{(-1)}^n{n}^{\frac{1}{2}}}{2^{2n}n!}{H}_{2n}\left(\frac{z}{2n^{\frac{1}{2}}}\right)=\frac{1}{{\pi }^{\frac{1}{2}}}\cos z,$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $!$: factorial (as in $n!$), $z$: complex variable and $n$: nonnegative integer

A&S Ref:

22.15.3

Referenced by:

§18.11(ii)

Permalink:

http://dlmf.nist.gov/18.11.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §18.11(ii), §18.11(ii), §18.11 and Ch.18

…

14: 18.27 $q$-Hahn Class

… ►

18.27.22 $$\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}\left(h_n(q^{\mathrm{\ell }};q)h_m(q^{\mathrm{\ell }};q)+h_n(-q^{\mathrm{\ell }};q)h_m(-q^{\mathrm{\ell }};q)\right){(q^{\mathrm{\ell }+1},-q^{\mathrm{\ell }+1};q)}_{\mathrm{\infty }}{q}^{\mathrm{\ell }}={(q;q)}_n{(q,-1,-q;q)}_{\mathrm{\infty }}{q}^{n(n-1)/2}{\delta }_{n,m}.$$

ⓘ

Symbols:

${\delta }_{j,k}$: Kronecker delta, $h_n(x;q)$: discrete $q$-Hermite I polynomial, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol, $q$: real variable, $\mathrm{\ell }$: nonnegative integer, $m$: nonnegative integer and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/18.27.E22

Encodings:

pMML, png, TeX

See also:

Annotations for §18.27(vii), §18.27(vii), §18.27 and Ch.18

… ►

18.27.23 $${\tilde{h}}_n(x;q)={(q;q)}_n\sum _{\mathrm{\ell }=0}^{\lfloor n/2\rfloor }\frac{{(-1)}^{\mathrm{\ell }}{q}^{-2n\mathrm{\ell }}{q}^{\mathrm{\ell }(2\mathrm{\ell }+1)}{x}^{n-2\mathrm{\ell }}}{{(q^2;q^2)}_{\mathrm{\ell }}{(q;q)}_{n-2\mathrm{\ell }}}=x^n{}_2{}^{}\varphi _1^{}(\genfrac{}{}{0pt}{}{q^{-n},q^{-n+1}}{0};q^2,-x^{-2}{q}^2).$$

ⓘ

Defines:

${\tilde{h}}_n(x;q)$: discrete $q$-Hermite II polynomial

Symbols:

$\lfloor x\rfloor$: floor of $x$ , ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${}_{r+1}{}^{}\varphi _s^{}(a_0,\mathrm{\dots },a_r;b_1,\mathrm{\dots },b_s;q,z)$ or ${}_{r+1}{}^{}\varphi _s^{}(\genfrac{}{}{0pt}{}{a_0,\mathrm{\dots },a_r}{b_1,\mathrm{\dots },b_s};q,z)$: basic hypergeometric (or $q$-hypergeometric) function, $q$: real variable, $\mathrm{\ell }$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/18.27.E23

Encodings:

pMML, png, TeX

See also:

Annotations for §18.27(vii), §18.27(vii), §18.27 and Ch.18

►

18.27.24 $$\sum _{\mathrm{\ell }=-\mathrm{\infty }}^{\mathrm{\infty }}\left({\tilde{h}}_n(c{q}^{\mathrm{\ell }};q){\tilde{h}}_m(c{q}^{\mathrm{\ell }};q)+{\tilde{h}}_n(-c{q}^{\mathrm{\ell }};q){\tilde{h}}_m(-c{q}^{\mathrm{\ell }};q)\right)\frac{q^{\mathrm{\ell }}}{{(-c^2{q}^{2\mathrm{\ell }};q^2)}_{\mathrm{\infty }}}=2\frac{{(q^2,-c^{2}q,-c^{-2}q;q^2)}_{\mathrm{\infty }}}{{(q,-c^2,-c^{-2}{q}^2;q^2)}_{\mathrm{\infty }}}\frac{{(q;q)}_n}{q^{n^2}}{\delta }_{n,m},$$ $c>0$.

ⓘ

Symbols:

${\delta }_{j,k}$: Kronecker delta, ${\tilde{h}}_n(x;q)$: discrete $q$-Hermite II polynomial, ${(a;q)}_n$: $q$-Pochhammer symbol (or $q$-shifted factorial), ${(a_1,a_2,\mathrm{\dots },a_r;q)}_n$: multiple $q$-Pochhammer symbol, $q$: real variable, $\mathrm{\ell }$: nonnegative integer, $m$: nonnegative integer and $n$: nonnegative integer

Permalink:

http://dlmf.nist.gov/18.27.E24

Encodings:

pMML, png, TeX

See also:

Annotations for §18.27(vii), §18.27(vii), §18.27 and Ch.18

… ►

18.27.25 $$\underset{q\to 1}{lim}\frac{h_n({(1-q^2)}^{\frac{1}{2}}x;q)}{{\left(1-q^2\right)}^{n/2}}=2^{-n}{H}_n\left(x\right).$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, $h_n(x;q)$: discrete $q$-Hermite I polynomial, $q$: real variable, $n$: nonnegative integer and $x$: real variable

Source:

Koekoek et al. (2010, (14.28.12))

Referenced by:

§18.27(vii), §18.27(vii), Erratum (V1.2.0) Section 18.27

Permalink:

http://dlmf.nist.gov/18.27.E25

Encodings:

pMML, png, TeX

Addition (effective with 1.2.0):

This equation was added.

See also:

Annotations for §18.27(vii), §18.27(vii), §18.27 and Ch.18

►

18.27.26 $$\underset{q\to 1}{lim}\frac{{\tilde{h}}_n({(1-q^2)}^{\frac{1}{2}}x;q)}{{\left(1-q^2\right)}^{n/2}}=2^{-n}{H}_n\left(x\right).$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, ${\tilde{h}}_n(x;q)$: discrete $q$-Hermite II polynomial, $q$: real variable, $n$: nonnegative integer and $x$: real variable

Source:

Koekoek et al. (2010, (14.29.14))

Referenced by:

§18.27(vii), §18.27(vii), Erratum (V1.2.0) Section 18.27

Permalink:

http://dlmf.nist.gov/18.27.E26

Encodings:

pMML, png, TeX

Addition (effective with 1.2.0):

This equation was added.

See also:

Annotations for §18.27(vii), §18.27(vii), §18.27 and Ch.18

15: 18.18 Sums

… ►

Hermite

… ►

Hermite

… ►

Hermite

… ►

Hermite

… ►

Hermite

…

16: 18.1 Notation

… ►

Hermite: $H_n\left(x\right)$, ${\mathrm{𝐻𝑒}}_n\left(x\right)$.

… ►

Discrete $q$-Hermite I: $h_n(x;q)$.

►

Discrete $q$-Hermite II: ${\tilde{h}}_n(x;q)$.

… ►

Continuous $q$-Hermite: $H_n\left(x|q\right)$.

►

Continuous $q^{-1}$-Hermite: $h_n\left(x|q\right)$

…

17: 18.9 Recurrence Relations and Derivatives

… ►

Table 18.9.1: Classical OP’s: recurrence relations (18.9.1).

► ►►►►

$p_n(x)$	$A_n$	$B_n$	$C_n$
…
$H_n\left(x\right)$	$2$	$0$	$2n$
${\mathrm{𝐻𝑒}}_n\left(x\right)$	$1$	$0$	$n$

►

… ►

Table 18.9.2: Classical OP’s: recurrence relations (18.9.2_1).

► ►►►

$p_n(x)$	$a_n$	$b_n$	$c_n$
…
$H_n\left(x\right)$	$\frac{1}{2}$	$0$	$n$

►

… ►

Hermite

… ►

18.9.27 $$\frac{d}{dx}{\mathrm{𝐻𝑒}}_n\left(x\right)=n{\mathrm{𝐻𝑒}}_{n-1}\left(x\right),$$

ⓘ

Symbols:

${\mathrm{𝐻𝑒}}_n\left(x\right)$: Hermite polynomial, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.8.7

Permalink:

http://dlmf.nist.gov/18.9.E27

Encodings:

pMML, png, TeX

See also:

Annotations for §18.9(iii), §18.9(iii), §18.9 and Ch.18

…

18: 18.10 Integral Representations

… ►

Hermite

… ►for the Jacobi, Laguerre, and Hermite polynomials. … ►

Table 18.10.1: Classical OP’s: contour integral representations (18.10.8).

► ►►►►

$p_n(x)$	$g_0(x)$	$g_1(z,x)$	$g_2(z,x)$	$c$	Conditions
…
$H_n\left(x\right)/n!$	$1$	$z^{-1}$	${\mathrm{e}}^{2xz-z^2}$	$0$
${\mathrm{𝐻𝑒}}_n\left(x\right)/n!$	$1$	$z^{-1}$	${\mathrm{e}}^{xz-\frac{1}{2}{z}^2}$	$0$

►

… ►

Hermite

…

19: 13.18 Relations to Other Functions

… ►

Hermite Polynomials

►

13.18.14 $$M_{\frac{1}{4}+n,-\frac{1}{4}}\left(z^2\right)={(-1)}^n\frac{n!}{(2n)!}{\mathrm{e}}^{-\frac{1}{2}{z}^2}\sqrt{z}{H}_{2n}\left(z\right),$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, $M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $n$: nonnegative integer and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.18.E14

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(v), §13.18(v), §13.18 and Ch.13

►

13.18.15 $$M_{\frac{3}{4}+n,\frac{1}{4}}\left(z^2\right)={(-1)}^n\frac{n!}{(2n+1)!}\frac{{\mathrm{e}}^{-\frac{1}{2}{z}^2}\sqrt{z}}{2}{H}_{2n+1}\left(z\right),$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, $M_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $n$: nonnegative integer and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.18.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(v), §13.18(v), §13.18 and Ch.13

►

13.18.16 $$W_{\frac{1}{4}+\frac{1}{2}n,\frac{1}{4}}\left(z^2\right)=2^{-n}{\mathrm{e}}^{-\frac{1}{2}{z}^2}\sqrt{z}{H}_n\left(z\right).$$

ⓘ

Symbols:

$H_n\left(x\right)$: Hermite polynomial, $W_{\kappa ,\mu }\left(z\right)$: Whittaker confluent hypergeometric function, $\mathrm{e}$: base of natural logarithm, $n$: nonnegative integer and $z$: complex variable

Permalink:

http://dlmf.nist.gov/13.18.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §13.18(v), §13.18(v), §13.18 and Ch.13

…

20: 18.30 Associated OP’s

… ►

§18.30(iv) Associated Hermite Polynomials

►The recursion relation for the associated Hermite polynomials, see (18.30.2), and (18.30.3), is ►

$H_{-1}(x;c)=0,$

►

$H_0(x;c)=1,$

… ►

18.30.13 $$H_{n+1}(x;c)=2x{H}_n(x;c)-2(n+c)H_{n-1}(x;c),$$ $n=0,1,\mathrm{\dots }$.

ⓘ

Symbols:

$H_n(x;c)$: associated Hermite polynomial, $n$: nonnegative integer and $x$: real variable

Referenced by:

(18.30.20)

Permalink:

http://dlmf.nist.gov/18.30.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §18.30(iv), §18.30 and Ch.18

…