Askey scheme for orthogonal polynomials

SearchAdvancedHelp

(0.005 seconds)

1—10 of 11 matching pages

1: 18.21 Hahn Class: Interrelations

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

2: Richard A. Askey

… ►Published in 1985 in the Memoirs of the American Mathematical Society, it also introduced the directed graph of hypergeometric orthogonal polynomials commonly known as the Askey scheme. …

3: Bibliography T

… ►

The Askey scheme for hypergeometric orthogonal polynomials viewed from asymptotic analysis. J. Comput. Appl. Math. 133 (1-2), pp. 623–633.

ⓘ

External Links:

ISSN 0377-0427, Document, MathReview (P. N. Rathie), ZentralBlatt

Referenced by:

§18.24.

Encodings:

BibTeX

…

4: 18.19 Hahn Class: Definitions

§18.19 Hahn Class: Definitions

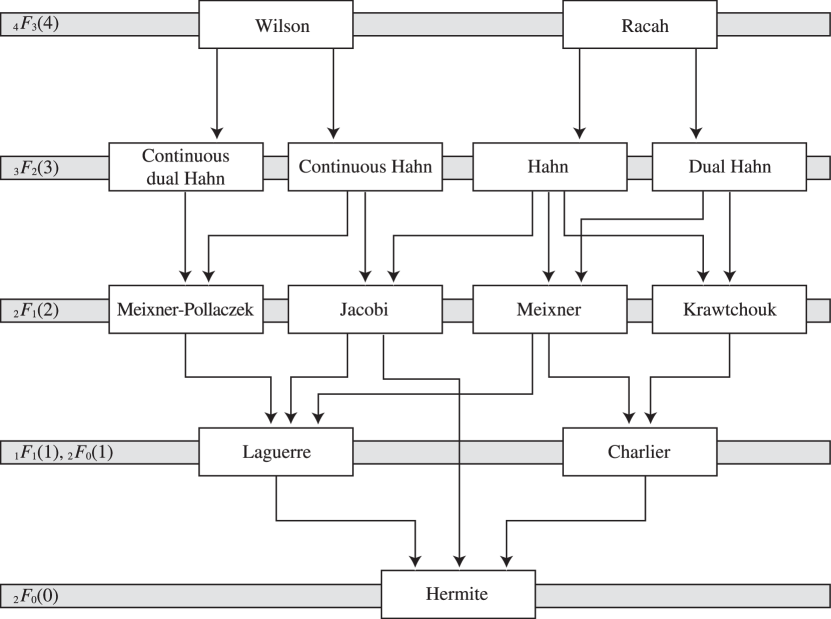
►The Askey scheme extends the three families of classical OP’s (Jacobi, Laguerre and Hermite) with eight further families of OP’s for which the role of the differentiation operator $\frac{d}{dx}$ in the case of the classical OP’s is played by a suitable difference operator. …In addition to the limit relations in §18.7(iii) there are limit relations involving the further families in the Askey scheme, see §§18.21(ii) and 18.26(ii). The Askey scheme, depicted in Figure 18.21.1, gives a graphical representation of these limits. … ►

Hahn, Krawtchouk, Meixner, and Charlier

…

5: Bibliography K

… ►

The Askey-scheme of hypergeometric orthogonal polynomials and its $q$-analogue. Technical report Technical Report 98-17, Delft University of Technology, Faculty of Information Technology and Systems, Department of Technical Mathematics and Informatics.

ⓘ

External Links:

FullText

Referenced by:

R. Koekoek, P. A. Lesky, and R. F. Swarttouw (2010).

Encodings:

BibTeX

…

6: 18.27 $q$-Hahn Class

… ►

§18.27(i) Introduction

… ►Together they form the $q$-Askey scheme. … ►All these systems of OP’s have orthogonality properties of the form … ►

§18.27(ii) $q$-Hahn Polynomials

… ►

Limit Relations

…

7: 18.26 Wilson Class: Continued

… ►Moreover, if one or more of the new parameters becomes zero, then the polynomial descends to a lower family in the Askey scheme.

8: 18.38 Mathematical Applications

… ►The Askey–Gasper inequality …also the case $\beta =0$ of (18.14.26), was used in de Branges’ proof of the long-standing Bieberbach conjecture concerning univalent functions on the unit disk in the complex plane. … ►

Group Representations

… ►Similar algebras can be associated with all families of OP’s in the $q$-Askey scheme and the Askey scheme. … ►Dunkl type operators and nonsymmetric polynomials have been associated with various other families in the Askey scheme and $q$-Askey scheme, in particular with Wilson polynomials, see Groenevelt (2007), and with Jacobi polynomials, see Koornwinder and Bouzeffour (2011, §7). …

9: Bibliography C

… ►

Work Group of Computational Mathematics, University of Kassel, Germany.

ⓘ

Notes:

Computer Algebra and Orthogonal Polynomials: a Web service using Maple for online generation of formulas and graphs of orthogonal polynomials belonging to the Askey scheme. For further information see Swarttouw (1997) and Koepf (1999).

External Links:

CAOP

Referenced by:

1st item.

Encodings:

BibTeX

…

10: Bibliography S

… ►

Orthogonal polynomials arising in the numerical evaluation of inverse Laplace transforms. Math. Tables Aids Comput. 9 (52), pp. 164–177.

ⓘ

External Links:

FullText, MathReview (S. C. van Veen), ZentralBlatt

Referenced by:

§3.5(viii).

Encodings:

BibTeX

… ►

Orthogonal Polynomials on the Unit Circle. Part 1: Classical Theory. American Mathematical Society Colloquium Publications, Vol. 54, American Mathematical Society, Providence, RI.

ⓘ

External Links:

ISBN 0-8218-3446-0, MathReview (P. L. Duren), ZentralBlatt

Referenced by:

(18.33.17), (18.33.18), (18.33.21), (18.33.22), (18.33.23), (18.33.24), (18.33.25), (18.33.26), (18.33.27), (18.33.28), (18.33.30), (18.33.31), (18.33.32), §18.33(vi), §18.33(i), §18.33(vi).

Encodings:

BibTeX

… ►

A computer implementation of the Askey-Wilson scheme. Technical Report 13 Vrije Universteit Amsterdam.

ⓘ

External Links:

FullText

Referenced by:

CAOP (website).

Encodings:

BibTeX

… ►

On certain special sets of orthogonal polynomials. Proc. Amer. Math. Soc. 1, pp. 731–737.

ⓘ

External Links:

ISSN 0002-9939, Document, Link, MathReview (A. C. Offord)

Referenced by:

§18.35(i).

Encodings:

BibTeX

►

Orthogonal Polynomials. 3rd edition, American Mathematical Society, New York.

ⓘ

Notes:

American Mathematical Society Colloquium Publications, Vol. 23

External Links:

MathReview (J. Burlak)

Referenced by:

Ch.14, §9.1, Notations A.

Encodings:

BibTeX

…