§36.4 Bifurcation Sets

Keywords:: bifurcation sets
Referenced by:: ¶ ‣ §36.5(ii), ¶ ‣ §36.5(ii)
Permalink:: http://dlmf.nist.gov/36.4

Contents

§36.4(i) Formulas
§36.4(ii) Visualizations

§36.4(i) Formulas

Keywords:: critical points
Permalink:: http://dlmf.nist.gov/36.4.i

¶ Critical Points for Cuspoids

These are real solutions $t_{j}(\mathbf{x})$ , $1\leq j\leq j_{{\max}}(\mathbf{x})\leq K+1$ , of

36.4.1 $\frac{\partial}{\partial t}\mathop{\Phi _{{K}}\/}\nolimits\!\left(t_{j}(\mathbf{x});\mathbf{x}\right)=0.$

Symbols:: $\mathop{\Phi _{{K}}\/}\nolimits\!\left(t;\mathbf{x}\right)$ : cuspoid catastrophe, $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $t$ : variable, $K$ : codimension and $t_{j}(\mathbf{x})$ : solutions
Referenced by:: §36.11, §36.12(i), ¶ ‣ §36.4(i), §36.5(i), §36.5(ii)
Permalink:: http://dlmf.nist.gov/36.4.E1
Encodings:: TeX, pMML, png

¶ Critical Points for Umbilics

These are real solutions $\{ s_{j}(\mathbf{x}),t_{j}(\mathbf{x})\}$ , $1\leq j\leq j_{{\max}}(\mathbf{x})\leq 4$ , of

36.4.2

$\frac{\partial}{\partial s}\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s_{j}(\mathbf{x}),t_{j}(\mathbf{x});\mathbf{x}\right)=0,$

$\frac{\partial}{\partial t}\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s_{j}(\mathbf{x}),t_{j}(\mathbf{x});\mathbf{x}\right)=0.$

Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $t$ : variable, $s$ : variable and $t_{j}(\mathbf{x})$ : solutions
Referenced by:: ¶ ‣ §36.4(i), §36.5(i)
Permalink:: http://dlmf.nist.gov/36.4.E2
Encodings:: TeX, TeX, pMML, pMML, png, png

¶ Bifurcation (Catastrophe) Set for Cuspoids

This is the codimension-one surface in $\mathbf{x}$ space where critical points coalesce, satisfying (36.4.1) and

36.4.3 $\frac{{\partial}^{2}}{{\partial t}^{2}}\mathop{\Phi _{{K}}\/}\nolimits\!\left(t;\mathbf{x}\right)=0.$

Symbols:: $\mathop{\Phi _{{K}}\/}\nolimits\!\left(t;\mathbf{x}\right)$ : cuspoid catastrophe, $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $t$ : variable and $K$ : codimension
Permalink:: http://dlmf.nist.gov/36.4.E3
Encodings:: TeX, pMML, png

¶ Bifurcation (Catastrophe) Set for Umbilics

This is the codimension-one surface in $\mathbf{x}$ space where critical points coalesce, satisfying (36.4.2) and

36.4.4 $\frac{{\partial}^{2}}{{\partial s}^{2}}\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s,t;\mathbf{x}\right)\frac{{\partial}^{2}}{{\partial t}^{2}}\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s,t;\mathbf{x}\right)-\left(\frac{{\partial}^{2}}{\partial s\partial t}\mathop{\Phi^{{(\mathrm{U})}}\/}\nolimits\!\left(s,t;\mathbf{x}\right)\right)^{2}=0.$

Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $\partial x$ : partial differential of $x$ , $t$ : variable and $s$ : variable
Permalink:: http://dlmf.nist.gov/36.4.E4
Encodings:: TeX, pMML, png

¶ Special Cases

Keywords:: cusp bifurcation set, elliptic umbilic bifurcation set, fold canonical integral, hyperbolic umbilic bifurcation set, swallowtail bifurcation set

$K=1$ , fold bifurcation set:

36.4.5 $x=0.$

Symbols:: $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E5
Encodings:: TeX, pMML, png

$K=2$ , cusp bifurcation set:

36.4.6 $27x^{2}=-8y^{3}.$

Symbols:: $y$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E6
Encodings:: TeX, pMML, png

$K=3$ , swallowtail bifurcation set:

36.4.7

$x=3t^{2}(z+5t^{2}),$

$y=-t(3z+10t^{2})$ , $-\infty<t<\infty$ .

Symbols:: $y$ : real parameter, $z$ : real parameter, $t$ : variable and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E7
Encodings:: TeX, TeX, pMML, pMML, png, png

Swallowtail self-intersection line:

36.4.8

$y=0,$

$z\leq 0,$

$x=\tfrac{9}{20}z^{2}.$

Symbols:: $y$ : real parameter, $z$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E8
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

Swallowtail cusp lines (ribs):

36.4.9

$z\leq 0,$

$x=-\tfrac{3}{20}z^{2},$

$10y^{2}=-4z^{3}.$

Symbols:: $y$ : real parameter, $z$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E9
Encodings:: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png

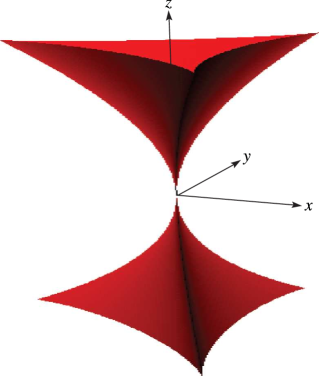
Elliptic umbilic bifurcation set (codimension three): for fixed $z$ , the section of the bifurcation set is a three-cusped astroid

36.4.10

$x=\tfrac{1}{3}z^{2}(-\mathop{\cos\/}\nolimits\!\left(2\phi\right)-2\mathop{\cos\/}\nolimits\phi),$

$y=\tfrac{1}{3}z^{2}(\mathop{\sin\/}\nolimits\!\left(2\phi\right)-2\mathop{\sin\/}\nolimits\phi)$ , $0\leq\phi\leq 2\pi$ .

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function, $y$ : real parameter, $z$ : real parameter and $x$ : real parameter
Referenced by:: §36.7(iii)
Permalink:: http://dlmf.nist.gov/36.4.E10
Encodings:: TeX, TeX, pMML, pMML, png, png

Elliptic umbilic cusp lines (ribs):

36.4.11 $x+iy=-z^{2}\mathop{\exp\/}\nolimits\!\left(\tfrac{2}{3}i\pi m\right),$ $m=0,1,2$ .

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $y$ : real parameter, $z$ : real parameter, $n$ : integer and $x$ : real parameter
Referenced by:: §36.7(iii)
Permalink:: http://dlmf.nist.gov/36.4.E11
Encodings:: TeX, pMML, png

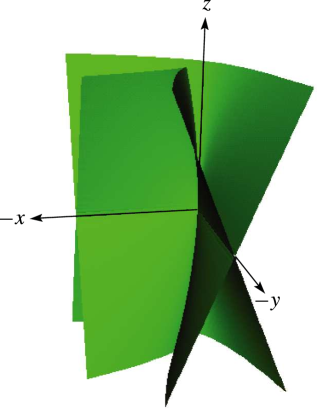
Hyperbolic umbilic bifurcation set (codimension three):

36.4.12

$x=-\tfrac{1}{12}z^{2}(\mathop{\exp\/}\nolimits\!\left(2\tau\right)\pm 2\mathop{\exp\/}\nolimits\!\left(-\tau\right)),$

$y=-\tfrac{1}{12}z^{2}(\mathop{\exp\/}\nolimits\!\left(-2\tau\right)\pm 2\mathop{\exp\/}\nolimits\!\left(\tau\right))$ , $-\infty\leq\tau<\infty.$

Symbols:: $\mathop{\exp\/}\nolimits z$ : exponential function, $y$ : real parameter, $z$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E12
Encodings:: TeX, TeX, pMML, pMML, png, png

The $+$ sign labels the cusped sheet; the $-$ sign labels the sheet that is smooth for $z\not=0$ (see Figure 36.4.4).

Hyperbolic umbilic cusp line (rib):

36.4.13 $x=y=-\tfrac{1}{4}z^{2}.$

Symbols:: $y$ : real parameter, $z$ : real parameter and $x$ : real parameter
Permalink:: http://dlmf.nist.gov/36.4.E13
Encodings:: TeX, pMML, png

For derivations of the results in this subsection see Poston and Stewart (1978, Chapter 9).

§36.4(ii) Visualizations

Notes:: These figures were generated by the authors.
Keywords:: bifurcation sets, cusp bifurcation set, elliptic umbilic bifurcation set, hyperbolic umbilic bifurcation set, swallowtail bifurcation set
Permalink:: http://dlmf.nist.gov/36.4.ii

See accompanying text

Figure 36.4.1: Bifurcation set of cusp catastrophe.

Magnify

Permalink:: http://dlmf.nist.gov/36.4.F1
Encodings:: pdf, png

See accompanying text

Figure 36.4.2: Bifurcation set of swallowtail catastrophe.

Magnify

Permalink:: http://dlmf.nist.gov/36.4.F2
Encodings:: pdf, png

See accompanying text

Figure 36.4.3: Bifurcation set of elliptic umbilic catastrophe.

Magnify

Permalink:: http://dlmf.nist.gov/36.4.F3
Encodings:: pdf, png

See accompanying text

Figure 36.4.4: Bifurcation set of hyperbolic umbilic catastrophe.

Magnify

Referenced by:: ¶ ‣ §36.4(i)
Permalink:: http://dlmf.nist.gov/36.4.F4
Encodings:: pdf, png