§34.4 Definition: $6j$ Symbol

Notes:: See Varshalovich et al. (1988, §9.2.4), de-Shalit and Talmi (1963, p. 131, Eq. (15.12)).
Keywords:: generalized hypergeometric functions, $6j$ symbols
Referenced by:: §16.4(iii)
Permalink:: http://dlmf.nist.gov/34.4

The $6j$ symbol is defined by the following double sum of products of $3j$ symbols:

34.4.1 $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}=\sum _{{m_{r}m^{{\prime}}_{s}}}(-1)^{{l_{{1}}+m^{{\prime}}_{{1}}+l_{{2}}+m^{{\prime}}_{{2}}+l_{{3}}+m^{{\prime}}_{{3}}}}\*\begin{pmatrix}j_{1}&j_{2}&j_{3}\\ m_{1}&m_{2}&m_{3}\end{pmatrix}\begin{pmatrix}j_{1}&l_{2}&l_{3}\\ m_{1}&m^{{\prime}}_{2}&-m^{{\prime}}_{3}\end{pmatrix}\begin{pmatrix}l_{1}&j_{2}&l_{3}\\ -m^{{\prime}}_{1}&m_{2}&m^{{\prime}}_{3}\end{pmatrix}\begin{pmatrix}l_{1}&l_{2}&j_{3}\\ m^{{\prime}}_{1}&-m^{{\prime}}_{2}&m_{3}\end{pmatrix},$

Defines:: $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}$ : $6j$ symbol
Symbols:: $\begin{pmatrix}j_{1}&j_{2}&j_{3}\\ m_{1}&m_{2}&m_{3}\end{pmatrix}$ : $3j$ symbol, $j,j_{r}$ : nonnegative integer, $l,l_{r}$ : nonnegative integer and $r$ : nonnegative integer
Referenced by:: §34.10, §34.4, §34.9
Permalink:: http://dlmf.nist.gov/34.4.E1
Encodings:: TeX, pMML, png

where the summation is taken over all admissible values of the $m$ ’s and $m^{{\prime}}$ ’s for each of the four $3j$ symbols; compare (34.2.2) and (34.2.3).

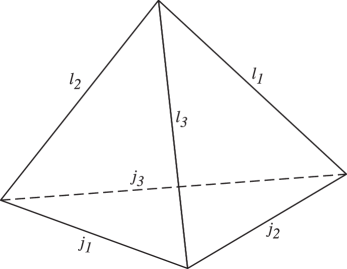
Except in degenerate cases the combination of the triangle inequalities for the four $3j$ symbols in (34.4.1) is equivalent to the existence of a tetrahedron (possibly degenerate) with edges of lengths $j_{1},j_{2},j_{3},l_{1},l_{2},l_{3}$ ; see Figure 34.4.1.

Figure 34.4.1: Tetrahedron corresponding to $6j$ symbol.

Symbols:: $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}$ : $6j$ symbol
Referenced by:: §34.4
Permalink:: http://dlmf.nist.gov/34.4.F1
Encodings:: pdf, png

The $6j$ symbol can be expressed as the finite sum

34.4.2 $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}=\sum _{{s}}\frac{(-1)^{{s}}(s+1)!}{(s-j_{{1}}-j_{{2}}-j_{{3}})!(s-j_{{1}}-l_{{2}}-l_{{3}})!(s-l_{{1}}-j_{{2}}-l_{{3}})!(s-l_{{1}}-l_{{2}}-j_{{3}})!}\*\frac{1}{(j_{{1}}+j_{{2}}+l_{{1}}+l_{{2}}-s)!(j_{{2}}+j_{{3}}+l_{{2}}+l_{{3}}-s)!(j_{{3}}+j_{{1}}+l_{{3}}+l_{{1}}-s)!},$

Symbols:: $!$ : $n!$ : factorial, $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}$ : $6j$ symbol, $j,j_{r}$ : nonnegative integer and $l,l_{r}$ : nonnegative integer
Permalink:: http://dlmf.nist.gov/34.4.E2
Encodings:: TeX, pMML, png

where the summation is over all nonnegative integers $s$ such that the arguments in the factorials are nonnegative.

Equivalently,

34.4.3 $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}={(-1)^{{j_{{1}}+j_{{3}}+l_{{1}}+l_{{3}}}}}\frac{\Delta(j_{{1}}j_{{2}}j_{{3}})\Delta(j_{{2}}l_{{1}}l_{{3}})(j_{{1}}-j_{{2}}+l_{{1}}+l_{{2}})!(-j_{{2}}+j_{{3}}+l_{{2}}+l_{{3}})!(j_{{1}}+j_{{3}}+l_{{1}}+l_{{3}}+1)!}{\Delta(j_{{1}}l_{{2}}l_{{3}})\Delta(j_{{3}}l_{{1}}l_{{2}})(j_{{1}}-j_{{2}}+j_{{3}})!(-j_{{2}}+l_{{1}}+l_{{3}})!(j_{{1}}+l_{{2}}+l_{{3}}+1)!(j_{{3}}+l_{{1}}+l_{{2}}+1)!}\*\mathop{{{}_{{4}}F_{{3}}}\/}\nolimits\!\left({-j_{{1}}+j_{{2}}-j_{{3}},j_{{2}}-l_{{1}}-l_{{3}},-j_{{1}}-l_{{2}}-l_{{3}}-1,-j_{{3}}-l_{{1}}-l_{{2}}-1\atop-j_{{1}}+j_{{2}}-l_{{1}}-l_{{2}},j_{{2}}-j_{{3}}-l_{{2}}-l_{{3}},-j_{{1}}-j_{{3}}-l_{{1}}-l_{{3}}-1};1\right),$

Symbols:: $\mathop{{{}_{{p}}F_{{q}}}\/}\nolimits\!\left({a_{1},\dots,a_{p}\atop b_{1},\dots,b_{q}};z\right)$ : generalized hypergeometric function, $!$ : $n!$ : factorial, $\begin{Bmatrix}j_{{1}}&j_{{2}}&j_{{3}}\\ l_{{1}}&l_{{2}}&l_{{3}}\end{Bmatrix}$ : $6j$ symbol, $j,j_{r}$ : nonnegative integer, $l,l_{r}$ : nonnegative integer and $\Delta(j_{1}j_{2}j_{3})$ : product
Permalink:: http://dlmf.nist.gov/34.4.E3
Encodings:: TeX, pMML, png

where $\mathop{{{}_{{4}}F_{{3}}}\/}\nolimits$ is defined as in §16.2.

For alternative expressions for the $6j$ symbol, written either as a finite sum or as other terminating generalized hypergeometric series $\mathop{{{}_{{4}}F_{{3}}}\/}\nolimits$ of unit argument, see Varshalovich et al. (1988, §§9.2.1, 9.2.3).

§34.4 Definition: Symbol

§34.4 Definition: $6j$ Symbol