spherical%20triangles

SearchAdvancedHelp

(0.002 seconds)

1—10 of 182 matching pages

1: 14.30 Spherical and Spheroidal Harmonics

… ►

§14.30(i) Definitions

… ► … ►

§14.30(iii) Sums

►

Distributional Completeness

… ►

2: 4.42 Solution of Triangles

§4.42 Solution of Triangles

►

§4.42(i) Planar Right Triangles

… ►

§4.42(ii) Planar Triangles

… ►

§4.42(iii) Spherical Triangles

►

►►

Figure 4.42.3: Spherical triangle. Magnify

…

3: 10.55 Continued Fractions

§10.55 Continued Fractions

►For continued fractions for ${𝗃}_{n+1}\left(z\right)/{𝗃}_n\left(z\right)$ and ${𝗂}_{n+1}^{(1)}\left(z\right)/{𝗂}_n^{(1)}\left(z\right)$ see Cuyt et al. (2008, pp. 350, 353, 362, 363, 367–369).

4: 10.73 Physical Applications

… ► … ►

§10.73(ii) Spherical Bessel Functions

►The functions ${𝗃}_n\left(x\right)$, ${𝗒}_n\left(x\right)$, ${𝗁}_n^{(1)}\left(x\right)$, and ${𝗁}_n^{(2)}\left(x\right)$ arise in the solution (again by separation of variables) of the Helmholtz equation in spherical coordinates $\rho ,\theta ,\varphi$ (§1.5(ii)): …With the spherical harmonic $Y_{\mathrm{\ell },m}\left(\theta ,\varphi \right)$ defined as in §14.30(i), the solutions are of the form $f=g_{\mathrm{\ell }}(k\rho )Y_{\mathrm{\ell },m}\left(\theta ,\varphi \right)$ with $g_{\mathrm{\ell }}={𝗃}_{\mathrm{\ell }}$, ${𝗒}_{\mathrm{\ell }}$, ${𝗁}_{\mathrm{\ell }}^{(1)}$, or ${𝗁}_{\mathrm{\ell }}^{(2)}$, depending on the boundary conditions. Accordingly, the spherical Bessel functions appear in all problems in three dimensions with spherical symmetry involving the scattering of electromagnetic radiation. …

5: 10.48 Graphs

§10.48 Graphs

… ►

►►

Figure 10.48.5: ${𝗂}_0^{(1)}\left(x\right)$, ${𝗂}_0^{(2)}\left(x\right)$, ${𝗄}_0\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.6: ${𝗂}_1^{(1)}\left(x\right),{𝗂}_1^{(2)}\left(x\right),{𝗄}_1\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.7: ${𝗂}_5^{(1)}\left(x\right)$, ${𝗂}_5^{(2)}\left(x\right)$, ${𝗄}_5\left(x\right)$, $0\le x\le 8$. Magnify

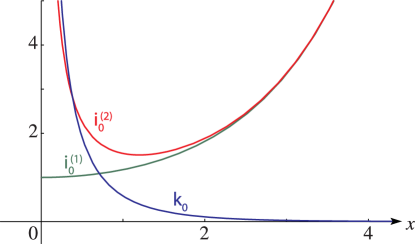6: 15.17 Mathematical Applications

… ►The quotient of two solutions of (15.10.1) maps the closed upper half-plane $\mathrm{\Im }z\ge 0$ conformally onto a curvilinear triangle. … ►First, as spherical functions on noncompact Riemannian symmetric spaces of rank one, but also as associated spherical functions, intertwining functions, matrix elements of SL$(2,ℝ)$, and spherical functions on certain nonsymmetric Gelfand pairs. …

7: 10.75 Tables

… ►

§10.75(ix) Spherical Bessel Functions, Modified Spherical Bessel Functions, and their Derivatives

►

The main tables in Abramowitz and Stegun (1964, Chapter 10) give ${𝗃}_n\left(x\right)$, ${𝗒}_n\left(x\right)$ $n=0(1)8$, $x=0(.1)10$, 5–8S; ${𝗃}_n\left(x\right)$, ${𝗒}_n\left(x\right)$ $n=0(1)20(10)50$, 100, $x=1,2,5,10,50,100$, 10S; ${𝗂}_n^{(1)}\left(x\right)$, ${𝗄}_n\left(x\right)$, $n=0,1,2$, $x=0(.1)5$, 4–9D; ${𝗂}_n^{(1)}\left(x\right)$, ${𝗄}_n\left(x\right)$, $n=0(1)20(10)50$, 100, $x=1,2,5,10,50,100$, 10S. (For the notation see §10.1 and §10.47(ii).)

►

Zhang and Jin (1996, pp. 296–305) tabulates ${𝗃}_n\left(x\right)$, ${𝗃}_n^{\prime }\left(x\right)$, ${𝗒}_n\left(x\right)$, ${𝗒}_n^{\prime }\left(x\right)$, ${𝗂}_n^{(1)}\left(x\right)$, $𝗂_n^{(1)}{}_{}{}^{\prime }\left(x\right)$, ${𝗄}_n\left(x\right)$, ${𝗄}_n^{\prime }\left(x\right)$, $n=0(1)10(10)30$, 50, 100, $x=1$, 5, 10, 25, 50, 100, 8S; $x{𝗃}_n\left(x\right)$, ${(x{𝗃}_n\left(x\right))}^{\prime }$, $x{𝗒}_n\left(x\right)$, ${(x{𝗒}_n\left(x\right))}^{\prime }$ (Riccati–Bessel functions and their derivatives), $n=0(1)10(10)30$, 50, 100, $x=1$, 5, 10, 25, 50, 100, 8S; real and imaginary parts of ${𝗃}_n\left(z\right)$, ${𝗃}_n^{\prime }\left(z\right)$, ${𝗒}_n\left(z\right)$, ${𝗒}_n^{\prime }\left(z\right)$, ${𝗂}_n^{(1)}\left(z\right)$, $𝗂_n^{(1)}{}_{}{}^{\prime }\left(z\right)$, ${𝗄}_n\left(z\right)$, ${𝗄}_n^{\prime }\left(z\right)$, $n=0(1)15$, 20(10)50, 100, $z=4+2\mathrm{i}$, $20+10\mathrm{i}$, 8S. (For the notation replace $j,y,\mathrm{i},k$ by $𝗃$, $𝗒$, ${𝗂}^{(1)}$, $𝗄$, respectively.)

►

§10.75(x) Zeros and Associated Values of Derivatives of Spherical Bessel Functions

… ►

Olver (1960) tabulates $a_{n,m}^{\prime }$, ${𝗃}_n\left(a_{n,m}^{\prime }\right)$, $b_{n,m}^{\prime }$, ${𝗒}_n\left(b_{n,m}^{\prime }\right)$, $n=1(1)20$, $m=1(1)50$, 8D. Also included are tables of the coefficients in the uniform asymptotic expansions of these zeros and associated values as $n\to \mathrm{\infty }$.

…

8: 10.52 Limiting Forms

§10.52 Limiting Forms

… ►

10.52.1 $${𝗃}_n\left(z\right),{𝗂}_n^{(1)}\left(z\right)\sim z^n/(2n+1)!!,$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $!!$: double factorial, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.4

Permalink:

http://dlmf.nist.gov/10.52.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

►

10.52.2 $$-{𝗒}_n\left(z\right),\mathrm{i}{𝗁}_n^{(1)}\left(z\right),-\mathrm{i}{𝗁}_n^{(2)}\left(z\right),{(-1)}^n{𝗂}_n^{(2)}\left(z\right),(2/\pi ){𝗄}_n\left(z\right)\sim (2n-1)!!/z^{n+1}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!!$: double factorial, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, ${𝗁}_n^{(1)}\left(z\right)$: spherical Bessel function of the third kind, ${𝗁}_n^{(2)}\left(z\right)$: spherical Bessel function of the third kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.5

Permalink:

http://dlmf.nist.gov/10.52.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

… ►

${𝗁}_n^{(1)}\left(z\right)\sim {\mathrm{i}}^{-n-1}{z}^{-1}{\mathrm{e}}^{\mathrm{i}z},$

… ►

10.52.5 $${𝗂}_n^{(1)}\left(z\right)\sim {𝗂}_n^{(2)}\left(z\right)\sim \frac{1}{2}{z}^{-1}{\mathrm{e}}^z,$$ ,

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{ph}$: phase, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $z$: complex variable and $\delta$: small positive constant

Permalink:

http://dlmf.nist.gov/10.52.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

…

9: 10.50 Wronskians and Cross-Products

§10.50 Wronskians and Cross-Products

… ►

$$𝒲\left\{{𝗁}_n^{(1)}\left(z\right),{𝗁}_n^{(2)}\left(z\right)\right\}=-2\mathrm{i}{z}^{-2}.$$

►

$$𝒲\left\{{𝗂}_n^{(1)}\left(z\right),{𝗂}_n^{(2)}\left(z\right)\right\}={(-1)}^{n+1}{z}^{-2},$$

►

$$𝒲\left\{{𝗂}_n^{(1)}\left(z\right),{𝗄}_n\left(z\right)\right\}=𝒲\left\{{𝗂}_n^{(2)}\left(z\right),{𝗄}_n\left(z\right)\right\}=-\frac{1}{2}\pi z^{-2}.$$

… ►Results corresponding to (10.50.3) and (10.50.4) for ${𝗂}_n^{(1)}\left(z\right)$ and ${𝗂}_n^{(2)}\left(z\right)$ are obtainable via (10.47.12).

10: 10.47 Definitions and Basic Properties

… ► … ►

Equation (10.47.1)

… ►

Equation (10.47.2)

… ► … ►

§10.47(iv) Interrelations

…