of complex argument

SearchAdvancedHelp

(0.001 seconds)

1—10 of 137 matching pages

1: 20.16 Software

… ►

§20.16(iii) Complex Argument and/or Parameter

…

2: 30.6 Functions of Complex Argument

§30.6 Functions of Complex Argument

►The solutions … ►

30.6.3 $$𝒲\left\{{\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2),{\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)\right\}=\frac{{(-1)}^m(n+m)!}{(1-z^2)(n-m)!}{A}_n^m({\gamma }^2)A_n^{-m}({\gamma }^2),$$

ⓘ

Symbols:

$𝒲$: Wronskian, $!$: factorial (as in $n!$), ${\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2)$: spheroidal wave function of complex argument, ${\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)$: spheroidal wave function of complex argument, $z$: complex variable, $m$: nonnegative integer, $n\ge m$: integer degree, $A_n^m({\gamma }^2)$ and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.6.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §30.6, §30.6 and Ch.30

… ►

30.6.4 $${\mathrm{𝑃𝑠}}_n^m(x\pm \mathrm{i}0,{\gamma }^2)={(\mp \mathrm{i})}^m{\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2),$$

ⓘ

Symbols:

$\mathrm{i}$: imaginary unit, ${\mathrm{𝑃𝑠}}_n^m(z,{\gamma }^2)$: spheroidal wave function of complex argument, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.6.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §30.6, §30.6 and Ch.30

►

30.6.5 $${\mathrm{𝑄𝑠}}_n^m(x\pm \mathrm{i}0,{\gamma }^2)={(\mp \mathrm{i})}^m\left({\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)\mp \frac{1}{2}\mathrm{i}\pi {\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{i}$: imaginary unit, ${\mathrm{𝑄𝑠}}_n^m(z,{\gamma }^2)$: spheroidal wave function of complex argument, ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the first kind, ${\mathrm{𝖰𝗌}}_n^m(x,{\gamma }^2)$: spheroidal wave function of the second kind, $x$: real variable, $m$: nonnegative integer, $n\ge m$: integer degree and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.6.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §30.6, §30.6 and Ch.30

…

3: 22.22 Software

… ►

§22.22(iii) Complex Argument

…

4: 23.24 Software

… ►

§23.24(iii) Complex Argument

…

5: 16.27 Software

… ►

§16.27(iii) Complex Argument and/or Parameters

…

6: 4.3 Graphics

… ►

§4.3(ii) Complex Arguments: Conformal Maps

… ►

§4.3(iii) Complex Arguments: Surfaces

… ►

►

►

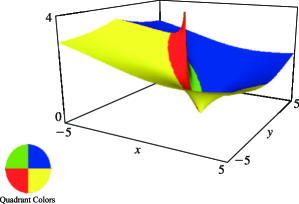
Figure 4.3.3: $\ln \left(x+\mathrm{i}y\right)$ (principal value). … Magnify 3D Help

►

►

►

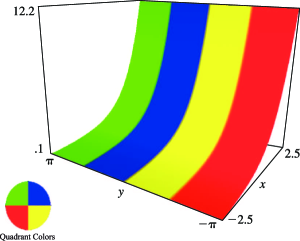
Figure 4.3.4: ${\mathrm{e}}^{x+\mathrm{i}y}$. Magnify 3D Help

7: 4.29 Graphics

… ►

§4.29(ii) Complex Arguments

…

8: 4.15 Graphics

… ►

§4.15(ii) Complex Arguments: Conformal Maps

… ►

§4.15(iii) Complex Arguments: Surfaces

… ►The corresponding surfaces for $\arccos \left(x+\mathrm{i}y\right)$, $\mathrm{arccot}\left(x+\mathrm{i}y\right)$, $\mathrm{arcsec}\left(x+\mathrm{i}y\right)$ can be visualized from Figures 4.15.9, 4.15.11, 4.15.13 with the aid of equations (4.23.16)–(4.23.18).

9: 10.77 Software

… ►

§10.77(iv) Bessel Functions–Integer or Half-Integer Order and Complex Arguments, including Kelvin Functions

… ►

§10.77(v) Bessel Functions–Real Order and Complex Argument (including Hankel Functions)

… ►

§10.77(vii) Bessel Functions–Complex Order and Real Argument

… ►

§10.77(viii) Bessel Functions–Complex Order and Argument

…

10: 14.26 Uniform Asymptotic Expansions

… ►For an extension of §14.15(iv) to complex argument and imaginary parameters, see Dunster (1990b). …