hypergeometric representations

SearchAdvancedHelp

(0.004 seconds)

1—10 of 70 matching pages

1: 8.5 Confluent Hypergeometric Representations

§8.5 Confluent Hypergeometric Representations

…

2: 14.21 Definitions and Basic Properties

… ►

§14.21(iii) Properties

… ►This includes, for example, the Wronskian relations (14.2.7)–(14.2.11); hypergeometric representations (14.3.6)–(14.3.10) and (14.3.15)–(14.3.20); results for integer orders (14.6.3)–(14.6.5), (14.6.7), (14.6.8), (14.7.6), (14.7.7), and (14.7.11)–(14.7.16); behavior at singularities (14.8.7)–(14.8.16); connection formulas (14.9.11)–(14.9.16); recurrence relations (14.10.3)–(14.10.7). …

3: 14.3 Definitions and Hypergeometric Representations

§14.3 Definitions and Hypergeometric Representations

… ►

§14.3(ii) Interval

… ►

§14.3(iii) Alternative Hypergeometric Representations

… ►For further hypergeometric representations of ${𝖰}_{\nu }^{\mu }\left(x\right)$ see Cohl et al. (2021). …

4: 14.19 Toroidal (or Ring) Functions

… ►

§14.19(ii) Hypergeometric Representations

…

5: 14.32 Methods of Computation

… ►In particular, for small or moderate values of the parameters $\mu$ and $\nu$ the power-series expansions of the various hypergeometric function representations given in §§14.3(i)–14.3(iii), 14.19(ii), and 14.20(i) can be selected in such a way that convergence is stable, and reasonably rapid, especially when the argument of the functions is real. …

6: 8.17 Incomplete Beta Functions

… ►

§8.17(ii) Hypergeometric Representations

…

7: 15.6 Integral Representations

§15.6 Integral Representations

►The function $𝐅(a,b;c;z)$ (not $F(a,b;c;z)$) has the following integral representations: … ►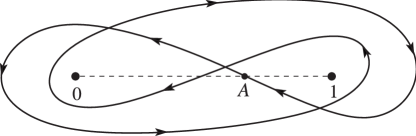

►►

Figure 15.6.1: $t$-plane. … Magnify

8: 8.27 Approximations

… ►

Luke (1969b, p. 186) gives hypergeometric polynomial representations that converge uniformly on compact subsets of the $z$-plane that exclude $z=0$ and are valid for .

…

9: 18.35 Pollaczek Polynomials

… ►

§18.35(i) Definition and Hypergeometric Representation

… ►we have the explicit representations …

10: 34.6 Definition: $\mathit{9}j$ Symbol

… ►The $\mathit{9}j$ symbol may also be written as a finite triple sum equivalent to a terminating generalized hypergeometric series of three variables with unit arguments. …