general lemniscatic case
♦
4 matching pages ♦
(0.001 seconds)
4 matching pages
1: 19.20 Special Cases
2: 23.22 Methods of Computation
…
►
(b)
…
If , then
23.22.2
There are 4 possible pairs (, ), corresponding to the 4 rotations of a square lattice. The lemniscatic case occurs when and .
3: 23.4 Graphics
…
►
►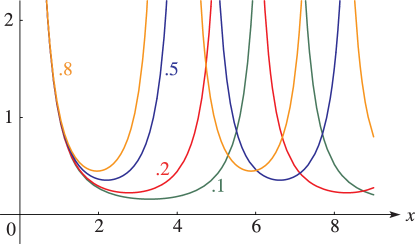 ►
►
Figure 23.4.1:
for , = 0.
…(Lemniscatic case.)
Magnify
…
►
► ►
►
Figure 23.4.3:
for , = 0.
…(Lemniscatic case.)
Magnify
…
►
► ►
►
Figure 23.4.5:
for , = 0.
…(Lemniscatic case.)
Magnify
…
§23.4(i) Real Variables
►Line graphs of the Weierstrass functions , , and , illustrating the lemniscatic and equianharmonic cases. … ► ►
►
 ►
►
 ►
►
