error-control function
(0.003 seconds)
11—20 of 957 matching pages
11: 15.2 Definitions and Analytical Properties
…
►
§15.2(i) Gauss Series
►The hypergeometric function is defined by the Gauss series … … ►On the circle of convergence, , the Gauss series: … ►§15.2(ii) Analytic Properties
…12: 5.12 Beta Function
§5.12 Beta Function
… ►Euler’s Beta Integral
… ►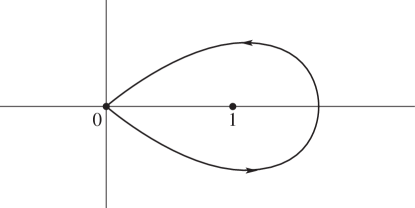 ►
►
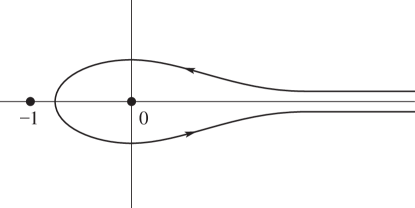 ►
►
Pochhammer’s Integral
…13: 14.20 Conical (or Mehler) Functions
§14.20 Conical (or Mehler) Functions
►§14.20(i) Definitions and Wronskians
… ► … ►§14.20(ii) Graphics
… ►§14.20(x) Zeros and Integrals
…14: 10.1 Special Notation
…
►(For other notation see Notation for the Special Functions.)
…
►For the spherical Bessel functions and modified spherical Bessel functions the order is a nonnegative integer.
For the other functions when the order is replaced by , it can be any integer.
For the Kelvin functions the order is always assumed to be real.
…
►For older notations see British Association for the Advancement of Science (1937, pp. xix–xx) and Watson (1944, Chapters 1–3).
15: 4.2 Definitions
16: 25.1 Special Notation
…
►(For other notation see Notation for the Special Functions.)
►
►
►The main function treated in this chapter is the Riemann zeta function
.
…
►The main related functions are the Hurwitz zeta function
, the dilogarithm , the polylogarithm (also known as Jonquière’s function
), Lerch’s transcendent , and the Dirichlet -functions
.
| nonnegative integers. | |
| … | |
| primes | on function symbols: derivatives with respect to argument. |
17: 12.1 Special Notation
…
►(For other notation see Notation for the Special Functions.)
…
►Unless otherwise noted, primes indicate derivatives with respect to the variable, and fractional powers take their principal values.
►The main functions treated in this chapter are the parabolic cylinder functions (PCFs), also known as Weber parabolic cylinder functions: , , , and .
…An older notation, due to Whittaker (1902), for is .
…
18: 17.1 Special Notation
§17.1 Special Notation
►(For other notation see Notation for the Special Functions.) ►| nonnegative integers. | |
| … | |
