accessory%20parameter

SearchAdvancedHelp

(0.002 seconds)

11—20 of 444 matching pages

11: 28.16 Asymptotic Expansions for Large $q$

… ►

28.16.1 $${\lambda }_{\nu }\left(h^2\right)\sim -2h^2+2sh-\frac{1}{8}(s^2+1)-\frac{1}{2^{7}h}(s^3+3s)-\frac{1}{2^{12}{h}^2}(5s^4+34s^2+9)-\frac{1}{2^{17}{h}^3}(33s^5+410s^3+405s)-\frac{1}{2^{20}{h}^4}(63s^6+1260s^4+2943s^2+486)-\frac{1}{2^{25}{h}^5}(527s^7+15617s^5+69001s^3+41607s)+\mathrm{\cdots }.$$

ⓘ

Symbols:

${\lambda }_{\nu +2n}\left(q\right)$: eigenvalues of Mathieu equation, $\sim$: Poincaré asymptotic expansion, $h$: parameter and $\nu$: complex parameter

Permalink:

http://dlmf.nist.gov/28.16.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §28.16 and Ch.28

…

12: 36.4 Bifurcation Sets

… ►

36.4.5 $$x=0.$$

ⓘ

Symbols:

$x$: real parameter

Permalink:

http://dlmf.nist.gov/36.4.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §36.4(i), §36.4(i), §36.4 and Ch.36

… ►

36.4.6 $$27x^2=-8y^3.$$

ⓘ

Symbols:

$y$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.4.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §36.4(i), §36.4(i), §36.4 and Ch.36

… ►

$x=\frac{9}{20}{z}^2.$

… ►

$x=-\frac{3}{20}{z}^2,$

… ►

36.4.13 $$x=y=-\frac{1}{4}{z}^2.$$

ⓘ

Symbols:

$y$: real parameter, $z$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.4.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §36.4(i), §36.4(i), §36.4 and Ch.36

…

13: 36.5 Stokes Sets

… ►

36.5.2 $$y^3=\frac{27}{4}\left(\sqrt{27}-5\right)x^2=1.32403x^2.$$

ⓘ

Symbols:

$y$: real parameter and $x$: real parameter

Permalink:

http://dlmf.nist.gov/36.5.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §36.5(ii), §36.5(ii), §36.5 and Ch.36

… ►

36.5.4 $$80x^5-40x^4-55x^3+5x^2+20x-1=0,$$

ⓘ

Symbols:

$x$: real parameter

Permalink:

http://dlmf.nist.gov/36.5.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §36.5(ii), §36.5(ii), §36.5 and Ch.36

… ►

36.5.7 $$X=\frac{9}{20}+20u^4-\frac{Y^2}{20u^2}+6u^2\mathrm{sign}\left(z\right),$$

ⓘ

Symbols:

$\mathrm{sign}x$: sign of, $z$: real parameter, $X$: scaled coordinate and $Y$: scaled coordinate

Permalink:

http://dlmf.nist.gov/36.5.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §36.5(ii), §36.5(ii), §36.5 and Ch.36

… ►

36.5.11 $$\frac{x}{z^2}=-1-12u^2+8u-\left|\frac{y}{z^2}\right|\frac{\frac{1}{3}-u}{{\left(u\left(\frac{2}{3}-u\right)\right)}^{1/2}}.$$

ⓘ

Symbols:

$y$: real parameter, $z$: real parameter and $x$: real parameter

Referenced by:

§36.5(iv)

Permalink:

http://dlmf.nist.gov/36.5.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §36.5(iii), §36.5(iii), §36.5 and Ch.36

… ►

36.5.12 $$8u^3-4u^2-\left|\frac{y}{3z^2}\right|{\left(\frac{u}{\frac{2}{3}-u}\right)}^{1/2}=\frac{y^2}{6w{z}^4}-2w^3-2w^2,$$

ⓘ

Symbols:

$y$: real parameter, $z$: real parameter and $w$: quantity

Permalink:

http://dlmf.nist.gov/36.5.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §36.5(iii), §36.5(iii), §36.5 and Ch.36

…

14: 27.2 Functions

… ►Euclid’s Elements (Euclid (1908, Book IX, Proposition 20)) gives an elegant proof that there are infinitely many primes. … ►

27.2.10 $${\sigma }_{\alpha }\left(n\right)=\sum _{d|n}{d}^{\alpha },$$

ⓘ

Defines:

${\sigma }_{\alpha }\left(n\right)$: sum of powers of divisors of a number

Symbols:

$d$: positive integer, $n$: positive integer and $\alpha$: parameter

A&S Ref:

24.3.3 I.A

Referenced by:

§27.14(ii)

Permalink:

http://dlmf.nist.gov/27.2.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §27.2(i), §27.2 and Ch.27

►is the sum of the $\alpha$th powers of the divisors of $n$, where the exponent $\alpha$ can be real or complex. … ►

Table 27.2.2: Functions related to division.

► ►►►►

$n$	$\varphi \left(n\right)$	$d\left(n\right)$	$\sigma \left(n\right)$	$n$	$\varphi \left(n\right)$	$d\left(n\right)$	$\sigma \left(n\right)$	$n$	$\varphi \left(n\right)$	$d\left(n\right)$	$\sigma \left(n\right)$	$n$	$\varphi \left(n\right)$	$d\left(n\right)$	$\sigma \left(n\right)$
…
5	4	2	6	18	6	6	39	31	30	2	32	44	20	6	84
…
7	6	2	8	20	8	6	42	33	20	4	48	46	22	4	72
…

►

15: 28.1 Special Notation

… ► ►►►►

$m,n$	integers.
…
$\nu$	order of the Mathieu function or modified Mathieu function. (When $\nu$ is an integer it is often replaced by $n$.)
…
$a,q,h$	real or complex parameters of Mathieu’s equation with $q=h^2$.
…

… ►Alternative notations for the parameters $a$ and $q$ are shown in Table 28.1.1. ►

Table 28.1.1: Notations for parameters in Mathieu’s equation.

► ►►

Reference	$a$	$q$
…

►

… ►

Abramowitz and Stegun (1964, Chapter 20)

…

16: 25.12 Polylogarithms

… ►

►►

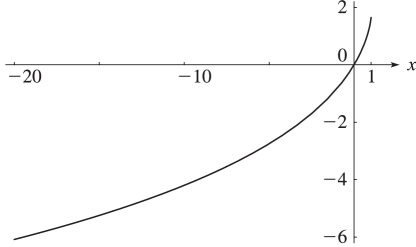
Figure 25.12.1: Dilogarithm function ${\mathrm{Li}}_2\left(x\right)$, Magnify

►

►

►

Figure 25.12.2: Absolute value of the dilogarithm function $\left|{\mathrm{Li}}_2\left(x+\mathrm{i}y\right)\right|$, $-20\le x\le 20$, $-20\le y\le 20$. … Magnify 3D Help

… ►

25.12.13 $${\mathrm{Li}}_s\left({\mathrm{e}}^{2\pi \mathrm{i}a}\right)+{\mathrm{e}}^{\pi \mathrm{i}s}{\mathrm{Li}}_s\left({\mathrm{e}}^{-2\pi \mathrm{i}a}\right)=\frac{{(2\pi )}^s{\mathrm{e}}^{\pi \mathrm{i}s/2}}{\mathrm{\Gamma }\left(s\right)}\zeta (1-s,a),$$

ⓘ

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function, $\zeta (s,a)$: Hurwitz zeta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $(a,b)$: open interval, ${\mathrm{Li}}_s\left(z\right)$: polylogarithm, $a$: real or complex parameter, $s$: complex variable and $z$: complex variable

Source:

Erdélyi et al. (1953a, (1.11.16), p. 31); with ${\mathrm{Li}}_s\left(z\right)=F(z,s)$, $z={\mathrm{e}}^{2\pi \mathrm{i}a}$

Referenced by:

§25.12(ii)

Permalink:

http://dlmf.nist.gov/25.12.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §25.12(ii), §25.12(ii), §25.12 and Ch.25

…

17: 8.17 Incomplete Beta Functions

… ►Throughout §§8.17 and 8.18 we assume that $a>0$, $b>0$, and $0\le x\le 1$. … ►

8.17.4 $$I_x(a,b)=1-I_{1-x}(b,a).$$

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter and $x$: variable

A&S Ref:

6.6.3 (Symmetry relation)

Referenced by:

§8.17(v), §8.18(i)

Permalink:

http://dlmf.nist.gov/8.17.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(i), §8.17 and Ch.8

… ►With $a>0$, $b>0$, and , … ►

8.17.13 $$(a+b)I_x(a,b)=a{I}_x(a+1,b)+b{I}_x(a,b+1),$$

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $a$: parameter, $b$: parameter and $x$: variable

A&S Ref:

6.6.7

Permalink:

http://dlmf.nist.gov/8.17.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §8.17(iv), §8.17 and Ch.8

… ►

8.17.24 $$I_x(m,n)={(1-x)}^n\sum _{j=m}^{\mathrm{\infty }}\left(\genfrac{}{}{0.0pt}{}{n+j-1}{j}\right)x^j,$$ $m,n$ positive integers; .

ⓘ

Symbols:

$I_x(a,b)$: incomplete beta function, $\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$: binomial coefficient, $n$: nonnegative integer and $x$: variable

A&S Ref:

26.5.26 (The upper limit of summation has been corrected.)

Referenced by:

§8.17(i), Erratum (V1.0.5) for Chapters 8, 20, 36

Permalink:

http://dlmf.nist.gov/8.17.E24

Encodings:

pMML, png, TeX

Addition (effective with 1.0.5):

This equation is the same as Equation (26.5.26) of Abramowitz and Stegun (1964), except that the upper limit of the summation has been corrected to $\mathrm{\infty }$.

Suggested 2011-03-23 by Stephen Bourn

See also:

Annotations for §8.17(vii), §8.17 and Ch.8

…

18: 8 Incomplete Gamma and Related
Functions

…

19: 28 Mathieu Functions and Hill’s Equation

…

20: 8.26 Tables

… ►

Khamis (1965) tabulates $P(a,x)$ for $a=0.05(.05)10(.1)20(.25)70$, $0.0001\le x\le 250$ to 10D.

… ►

Abramowitz and Stegun (1964, pp. 245–248) tabulates $E_n\left(x\right)$ for $n=2,3,4,10,20$, $x=0(.01)2$ to 7D; also $(x+n){\mathrm{e}}^x{E}_n\left(x\right)$ for $n=2,3,4,10,20$, $x^{-1}=0(.01)0.1(.05)0.5$ to 6S.

… ►

Pagurova (1961) tabulates $E_n\left(x\right)$ for $n=0(1)20$, $x=0(.01)2(.1)10$ to 4-9S; ${\mathrm{e}}^x{E}_n\left(x\right)$ for $n=2(1)10$, $x=10(.1)20$ to 7D; ${\mathrm{e}}^x{E}_p\left(x\right)$ for $p=0(.1)1$, $x=0.01(.01)7(.05)12(.1)20$ to 7S or 7D.

… ►

Zhang and Jin (1996, Table 19.1) tabulates $E_n\left(x\right)$ for $n=1,2,3,5,10,15,20$, $x=0(.1)1,1.5,2,3,5,10,20,30,50,100$ to 7D or 8S.