Basset%20integral

SearchAdvancedHelp

(0.002 seconds)

11—20 of 471 matching pages

11: 8.26 Tables

… ►

Khamis (1965) tabulates $P(a,x)$ for $a=0.05(.05)10(.1)20(.25)70$, $0.0001\le x\le 250$ to 10D.

… ►

§8.26(iv) Generalized Exponential Integral

►

Abramowitz and Stegun (1964, pp. 245–248) tabulates $E_n\left(x\right)$ for $n=2,3,4,10,20$, $x=0(.01)2$ to 7D; also $(x+n){\mathrm{e}}^x{E}_n\left(x\right)$ for $n=2,3,4,10,20$, $x^{-1}=0(.01)0.1(.05)0.5$ to 6S.

… ►

Pagurova (1961) tabulates $E_n\left(x\right)$ for $n=0(1)20$, $x=0(.01)2(.1)10$ to 4-9S; ${\mathrm{e}}^x{E}_n\left(x\right)$ for $n=2(1)10$, $x=10(.1)20$ to 7D; ${\mathrm{e}}^x{E}_p\left(x\right)$ for $p=0(.1)1$, $x=0.01(.01)7(.05)12(.1)20$ to 7S or 7D.

… ►

Zhang and Jin (1996, Table 19.1) tabulates $E_n\left(x\right)$ for $n=1,2,3,5,10,15,20$, $x=0(.1)1,1.5,2,3,5,10,20,30,50,100$ to 7D or 8S.

12: 6.19 Tables

… ►

§6.19(ii) Real Variables

►

Abramowitz and Stegun (1964, Chapter 5) includes $x^{-1}\mathrm{Si}\left(x\right)$, $-x^{-2}\mathrm{Cin}\left(x\right)$, $x^{-1}\mathrm{Ein}\left(x\right)$, $-x^{-1}\mathrm{Ein}\left(-x\right)$, $x=0(.01)0.5$; $\mathrm{Si}\left(x\right)$, $\mathrm{Ci}\left(x\right)$, $\mathrm{Ei}\left(x\right)$, $E_1\left(x\right)$, $x=0.5(.01)2$; $\mathrm{Si}\left(x\right)$, $\mathrm{Ci}\left(x\right)$, $x{\mathrm{e}}^{-x}\mathrm{Ei}\left(x\right)$, $x{\mathrm{e}}^x{E}_1\left(x\right)$, $x=2(.1)10$; $x\mathrm{f}\left(x\right)$, $x^2\mathrm{g}\left(x\right)$, $x{\mathrm{e}}^{-x}\mathrm{Ei}\left(x\right)$, $x{\mathrm{e}}^x{E}_1\left(x\right)$, $x^{-1}=0(.005)0.1$; $\mathrm{Si}\left(\pi x\right)$, $\mathrm{Cin}\left(\pi x\right)$, $x=0(.1)10$. Accuracy varies but is within the range 8S–11S.

►

Zhang and Jin (1996, pp. 652, 689) includes $\mathrm{Si}\left(x\right)$, $\mathrm{Ci}\left(x\right)$, $x=0(.5)20(2)30$, 8D; $\mathrm{Ei}\left(x\right)$, $E_1\left(x\right)$, $x=[0,100]$, 8S.

… ►

Abramowitz and Stegun (1964, Chapter 5) includes the real and imaginary parts of $z{\mathrm{e}}^z{E}_1\left(z\right)$, $x=-19(1)20$, $y=0(1)20$, 6D; ${\mathrm{e}}^z{E}_1\left(z\right)$, $x=-4(.5)-2$, $y=0(.2)1$, 6D; $E_1\left(z\right)+\ln z$, $x=-2(.5)2.5$, $y=0(.2)1$, 6D.

►

Zhang and Jin (1996, pp. 690–692) includes the real and imaginary parts of $E_1\left(z\right)$, $\pm x=0.5,1,3,5,10,15,20,50,100$, $y=0(.5)1(1)5(5)30,50,100$, 8S.

13: 36 Integrals with Coalescing Saddles

Chapter 36 Integrals with Coalescing Saddles

…

14: 6.20 Approximations

… ►

Hastings (1955) gives several minimax polynomial and rational approximations for $E_1\left(x\right)+\ln x$, $x{\mathrm{e}}^x{E}_1\left(x\right)$, and the auxiliary functions $\mathrm{f}\left(x\right)$ and $\mathrm{g}\left(x\right)$. These are included in Abramowitz and Stegun (1964, Ch. 5).

►

Cody and Thacher (1968) provides minimax rational approximations for $E_1\left(x\right)$, with accuracies up to 20S.

►

Cody and Thacher (1969) provides minimax rational approximations for $\mathrm{Ei}\left(x\right)$, with accuracies up to 20S.

►

MacLeod (1996b) provides rational approximations for the sine and cosine integrals and for the auxiliary functions $\mathrm{f}$ and $\mathrm{g}$, with accuracies up to 20S.

… ►

Luke and Wimp (1963) covers $\mathrm{Ei}\left(x\right)$ for $x\le -4$ (20D), and $\mathrm{Si}\left(x\right)$ and $\mathrm{Ci}\left(x\right)$ for $x\ge 4$ (20D).

…

15: 20 Theta Functions

Chapter 20 Theta Functions

…

16: Peter L. Walker

… ►Walker’s books are An Introduction to Complex Analysis, published by Hilger in 1974, The Theory of Fourier Series and Integrals, published by Wiley in 1986, Elliptic Functions. A Constructive Approach, published by Wiley in 1996, and Examples and Theorems in Analysis, published by Springer in 2004. … ►

20 Theta Functions

…

17: 7.24 Approximations

… ►

§7.24(i) Approximations in Terms of Elementary Functions

… ►

Cody (1969) provides minimax rational approximations for $\mathrm{erf}x$ and $\mathrm{erfc}x$. The maximum relative precision is about 20S.

►

Cody (1968) gives minimax rational approximations for the Fresnel integrals (maximum relative precision 19S); for a Fortran algorithm and comments see Snyder (1993).

►

Cody et al. (1970) gives minimax rational approximations to Dawson’s integral $F\left(x\right)$ (maximum relative precision 20S–22S).

… ►

Luke (1969b, vol. 2, pp. 422–435) gives main diagonal Padé approximations for $F\left(z\right)$, $\mathrm{erf}z$, $\mathrm{erfc}z$, $C\left(z\right)$, and $S\left(z\right)$; approximate errors are given for a selection of $z$-values.

18: 25.12 Polylogarithms

… ►The right-hand side is called Clausen’s integral. … ►

Integral Representation

… ►

§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

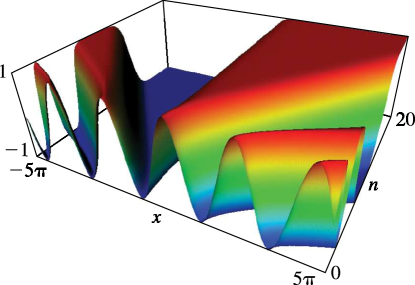
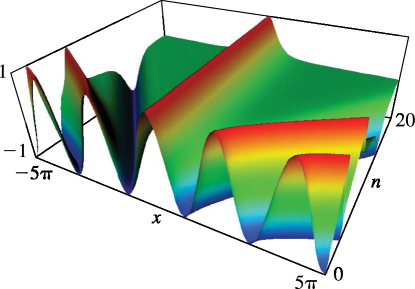
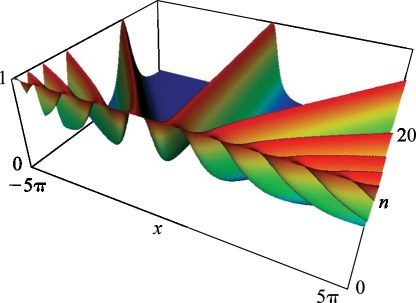
►The Fermi–Dirac and Bose–Einstein integrals are defined by … ►In terms of polylogarithms …

19: 22.3 Graphics

… ►

►

►

Figure 22.3.13: $\mathrm{sn}(x,k)$ for $k=1-{\mathrm{e}}^{-n}$, $n=0$ to 20, $-5\pi \le x\le 5\pi$. Magnify 3D Help

►

►

►

Figure 22.3.14: $\mathrm{cn}(x,k)$ for $k=1-{\mathrm{e}}^{-n}$, $n=0$ to 20, $-5\pi \le x\le 5\pi$. Magnify 3D Help

►

►

►

Figure 22.3.15: $\mathrm{dn}(x,k)$ for $k=1-{\mathrm{e}}^{-n}$, $n=0$ to 20, $-5\pi \le x\le 5\pi$. Magnify 3D Help

… ►

►►

Figure 22.3.28: Density plot of $|\mathrm{sn}(20,k)|$ as a function of complex $k^2$, $-10\le \mathrm{\Re }\left(k^2\right)\le 20$, $-10\le \mathrm{\Im }\left(k^2\right)\le 10$. Grayscale, running from 0 (black) to 10 (white), with $|\mathrm{sn}(20,k)|>10$ truncated to 10. … Magnify

…

20: 10.75 Tables

… ►

Achenbach (1986) tabulates $J_0\left(x\right)$, $J_1\left(x\right)$, $Y_0\left(x\right)$, $Y_1\left(x\right)$, $x=0(.1)8$, 20D or 18–20S.

… ►

Zhang and Jin (1996, p. 270) tabulates ${\int }_0^x{J}_0\left(t\right)dt$, ${\int }_0^x{t}^{-1}(1-J_0\left(t\right))dt$, ${\int }_0^x{Y}_0\left(t\right)dt$, ${\int }_x^{\mathrm{\infty }}{t}^{-1}{Y}_0\left(t\right)dt$, $x=0(.1)1(.5)20$, 8D.

… ►

Bickley et al. (1952) tabulates $x^{-n}{I}_n\left(x\right)$ or ${\mathrm{e}}^{-x}{I}_n\left(x\right)$, $x^n{K}_n\left(x\right)$ or ${\mathrm{e}}^x{K}_n\left(x\right)$, $n=2(1)20$, $x=0$(.01 or .1) 10(.1) 20, 8S; $I_n\left(x\right)$, $K_n\left(x\right)$, $n=0(1)20$, $x=0$ or $0.1(.1)20$, 10S.

… ►

Kerimov and Skorokhodov (1984b) tabulates all zeros of the principal values of $K_n\left(z\right)$ and $K_n^{\prime }\left(z\right)$, for $n=2(1)20$, 9S.

… ►

Zhang and Jin (1996, p. 271) tabulates ${\mathrm{e}}^{-x}{\int }_0^x{I}_0\left(t\right)dt$, ${\mathrm{e}}^{-x}{\int }_0^x{t}^{-1}(I_0\left(t\right)-1)dt$, ${\mathrm{e}}^x{\int }_x^{\mathrm{\infty }}{K}_0\left(t\right)dt$, $x{\mathrm{e}}^x{\int }_x^{\mathrm{\infty }}{t}^{-1}{K}_0\left(t\right)dt$, $x=0(.1)1(.5)20$, 8D.

…