3F2 functions of matrix argument

SearchAdvancedHelp

(0.004 seconds)

11—20 of 982 matching pages

11: 11.9 Lommel Functions

§11.9 Lommel Functions

… ►Provided that $\mu \pm \nu \ne -1,-3,-5,\mathrm{\dots }$, (11.9.1) has the general solution … ►When $\mu \pm \nu \ne -1,-2,-3,\mathrm{\dots }$, … ►

§11.9(iii) Asymptotic Expansion

… ►For further information on Lommel functions see Watson (1944, §§10.7–10.75) and Babister (1967, Chapter 3). …

12: 16.13 Appell Functions

§16.13 Appell Functions

►The following four functions of two real or complex variables $x$ and $y$ cannot be expressed as a product of two ${}_2{}^{}F_1^{}$ functions, in general, but they satisfy partial differential equations that resemble the hypergeometric differential equation (15.10.1): ►

16.13.1 $$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)=\sum _{m,n=0}^{\mathrm{\infty }}\frac{{\left(\alpha \right)}_{m+n}{\left(\beta \right)}_m{\left({\beta }^{\prime }\right)}_n}{{\left(\gamma \right)}_{m+n}m!n!}{x}^m{y}^n,$$ ,

ⓘ

Defines:

$F_1(\alpha ;\beta ,{\beta }^{\prime };\gamma ;x,y)$: first Appell function

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial) and $!$: factorial (as in $n!$)

Permalink:

http://dlmf.nist.gov/16.13.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §16.13 and Ch.16

… ►

16.13.3 $$F_3(\alpha ,{\alpha }^{\prime };\beta ,{\beta }^{\prime };\gamma ;x,y)=\sum _{m,n=0}^{\mathrm{\infty }}\frac{{\left(\alpha \right)}_m{\left({\alpha }^{\prime }\right)}_n{\left(\beta \right)}_m{\left({\beta }^{\prime }\right)}_n}{{\left(\gamma \right)}_{m+n}m!n!}{x}^m{y}^n,$$ ,

ⓘ

Defines:

$F_3(\alpha ,{\alpha }^{\prime };\beta ,{\beta }^{\prime };\gamma ;x,y)$: third Appell function

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial) and $!$: factorial (as in $n!$)

Permalink:

http://dlmf.nist.gov/16.13.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §16.13 and Ch.16

… ► …

13: 14.19 Toroidal (or Ring) Functions

§14.19 Toroidal (or Ring) Functions

►

§14.19(i) Introduction

… ►

§14.19(ii) Hypergeometric Representations

… ►

§14.19(iv) Sums

… ►

§14.19(v) Whipple’s Formula for Toroidal Functions

…

14: 5.15 Polygamma Functions

§5.15 Polygamma Functions

►The functions ${\psi }^{(n)}\left(z\right)$, $n=1,2,\mathrm{\dots }$, are called the polygamma functions. In particular, ${\psi }^{\prime }\left(z\right)$ is the trigamma function; ${\psi }^{\prime \prime }$, ${\psi }^{(3)}$, ${\psi }^{(4)}$ are the tetra-, penta-, and hexagamma functions respectively. Most properties of these functions follow straightforwardly by differentiation of properties of the psi function. … ►In (5.15.2)–(5.15.7) $n,m=1,2,3,\mathrm{\dots }$, and for $\zeta \left(n+1\right)$ see §25.6(i). …

15: 14.20 Conical (or Mehler) Functions

§14.20 Conical (or Mehler) Functions

… ► … ► ${\widehat{𝖰}}_{-\frac{1}{2}+\mathrm{i}\tau }^{-\mu }\left(x\right)$ exists except when $\mu =\frac{1}{2},\frac{3}{2},\mathrm{\dots }$ and $\tau =0$; compare §14.3(i). … ►For extensions to complex arguments (including the range ), asymptotic expansions, and explicit error bounds, see Dunster (1991). For the case of purely imaginary order and argument see Dunster (2013). …

16: 5.2 Definitions

… ►

§5.2(i) Gamma and Psi Functions

►

Euler’s Integral

… ►It is a meromorphic function with no zeros, and with simple poles of residue ${(-1)}^n/n!$ at $z=-n$. … ►

5.2.2 $$\psi \left(z\right)={\mathrm{\Gamma }}^{\prime }\left(z\right)/\mathrm{\Gamma }\left(z\right),$$ $z\ne 0,-1,-2,\mathrm{\dots }$.

ⓘ

Defines:

$\psi \left(z\right)$: psi (or digamma) function

Symbols:

$\mathrm{\Gamma }\left(z\right)$: gamma function and $z$: complex variable

A&S Ref:

6.3.1

Permalink:

http://dlmf.nist.gov/5.2.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §5.2(i), §5.2(i), §5.2 and Ch.5

… ►

5.2.3 $$\gamma =\underset{n\to \mathrm{\infty }}{lim}\left(1+\frac{1}{2}+\frac{1}{3}+\mathrm{\cdots }+\frac{1}{n}-\ln n\right)=\mathrm{0.57721\hspace{0.33em}56649\hspace{0.33em}01532\hspace{0.33em}86060}\mathrm{\dots }.$$

ⓘ

Defines:

$\gamma$: Euler’s constant

Symbols:

$\ln z$: principal branch of logarithm function and $n$: nonnegative integer

A&S Ref:

6.1.3 (where the 10D value is given, and Table 1.1 where the 24D value is given.)

Notes:

For more digits see OEIS Sequence A001620; see also Sloane (2003).

Referenced by:

§4.4(iii)

Permalink:

http://dlmf.nist.gov/5.2.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §5.2(ii), §5.2 and Ch.5

…

17: 31.1 Special Notation

… ►(For other notation see Notation for the Special Functions.) ► ►►

$x$, $y$	real variables.
…

►The main functions treated in this chapter are $H\mathrm{\ell }(a,q;\alpha ,\beta ,\gamma ,\delta ;z)$, $(s_1,s_2){\mathrm{𝐻𝑓}}_m(a,q_m;\alpha ,\beta ,\gamma ,\delta ;z)$, $(s_1,s_2){\mathrm{𝐻𝑓}}_m^{\nu }(a,q_m;\alpha ,\beta ,\gamma ,\delta ;z)$, and the polynomial ${\mathrm{𝐻𝑝}}_{n,m}(a,q_{n,m};-n,\beta ,\gamma ,\delta ;z)$. …Sometimes the parameters are suppressed.

18: 15.2 Definitions and Analytical Properties

… ►

§15.2(i) Gauss Series

►The hypergeometric function $F(a,b;c;z)$ is defined by the Gauss series … … ►On the circle of convergence, $|z|=1$, the Gauss series: … ►

§15.2(ii) Analytic Properties

…

19: 5.12 Beta Function

§5.12 Beta Function

… ►

Euler’s Beta Integral

… ►

►►

Figure 5.12.1: $t$-plane. Contour for first loop integral for the beta function. Magnify

… ►

►►

Figure 5.12.2: $t$-plane. Contour for second loop integral for the beta function. Magnify

►

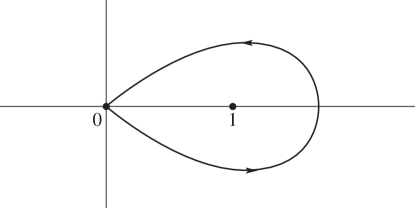
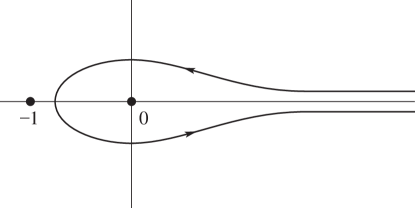
Pochhammer’s Integral

…

20: 10.1 Special Notation

… ►(For other notation see Notation for the Special Functions.) … ►For the spherical Bessel functions and modified spherical Bessel functions the order $n$ is a nonnegative integer. For the other functions when the order $\nu$ is replaced by $n$, it can be any integer. For the Kelvin functions the order $\nu$ is always assumed to be real. … ►For older notations see British Association for the Advancement of Science (1937, pp. xix–xx) and Watson (1944, Chapters 1–3).