cialis 5mg tabs 28 visit drive-in.co.za

SearchAdvancedHelp

Did you mean specialists 5mg abs 28 visit driver-main.aspx ?

(0.005 seconds)

1—10 of 304 matching pages

1: Simon Ruijsenaars

… ►

5 Gamma Function

►

28 Mathieu Functions and Hill’s Equation

2: 26.2 Basic Definitions

… ►If, for example, a permutation of the integers 1 through 6 is denoted by $256413$, then the cycles are $\left(1,2,5\right)$, $\left(3,6\right)$, and $\left(4\right)$. Here $\sigma (1)=2,\sigma (2)=5$, and $\sigma (5)=1$. … ►As an example, $\{1,3,4\}$, $\{2,6\}$, $\{5\}$ is a partition of $\{1,2,3,4,5,6\}$. … ►For the actual partitions ($\pi$) for $n=1(1)5$ see Table 26.4.1. … ►

Table 26.2.1: Partitions $p\left(n\right)$.

► ►►►

$n$	$p\left(n\right)$	$n$	$p\left(n\right)$	$n$	$p\left(n\right)$
…
4	5	21	792	38	26015
…

►

3: 26.9 Integer Partitions: Restricted Number and Part Size

… ►

Table 26.9.1: Partitions $p_k\left(n\right)$.

► ►►►►►

$n$	$k$
	…
4	0	1	3	4	5	5	5	5	5	5	5
5	0	1	3	5	6	7	7	7	7	7	7
…
9	0	1	5	12	18	23	26	28	29	30	30
…

►

… ►The conjugate to the example in Figure 26.9.1 is $6+5+4+2+1+1+1$. … ►

Figure 26.9.2: The partition $5+5+3+2$ represented as a lattice path.

…

4: 14.22 Graphics

… ►

►

►

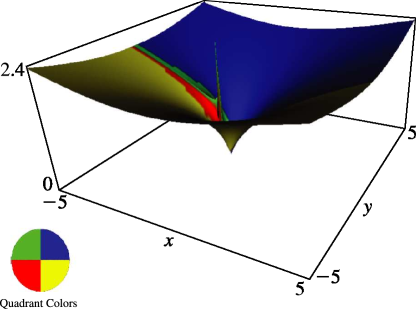
Figure 14.22.1: $P_{1/2}^0\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. … Magnify 3D Help

►

►

►

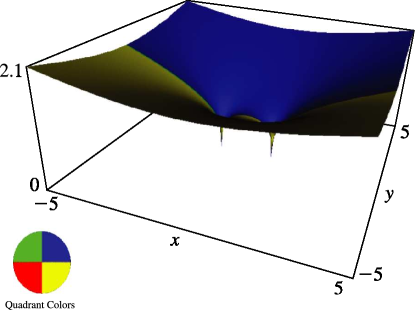
Figure 14.22.2: $P_{1/2}^{-1/2}\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. … Magnify 3D Help

►

►

►

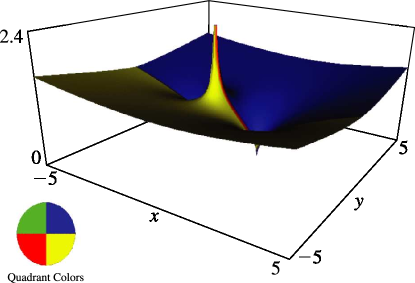
Figure 14.22.3: $P_{1/2}^{-1}\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. … Magnify 3D Help

►

►

►

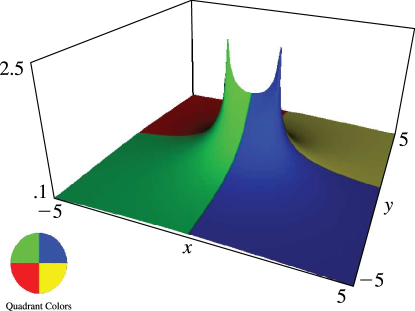
Figure 14.22.4: ${𝑸}_0^0\left(x+\mathrm{i}y\right)$, $-5\le x\le 5$, $-5\le y\le 5$. … Magnify 3D Help

5: 26.3 Lattice Paths: Binomial Coefficients

… ►

Table 26.3.1: Binomial coefficients $\left(\genfrac{}{}{0.0pt}{}{m}{n}\right)$.

► ►►►

$m$	$n$
	…
5	1	5	10	10	5	1
…

►

►

Table 26.3.2: Binomial coefficients $\left(\genfrac{}{}{0.0pt}{}{m+n}{m}\right)$ for lattice paths.

► ►►►►►►

$m$	$n$
	0	1	2	3	4	5	6	7	8
…
1	1	2	3	4	5	6	7	8	9
…
4	1	5	15	35	70	126	210	330	495
5	1	6	21	56	126	252	462	792	1287
…

►

…

6: 26.4 Lattice Paths: Multinomial Coefficients and Set Partitions

… ►Table 26.4.1 gives numerical values of multinomials and partitions $\lambda ,M_1,M_2,M_3$ for $1\le m\le n\le 5$. … ►

Table 26.4.1: Multinomials and partitions.

► ►►►►►►

$n$	$m$	$\lambda$	$M_1$	$M_2$	$M_3$
…
$5$	$1$	$5^1$	$1$	$24$	$1$
$5$	$2$	$1^1,4^1$	$5$	$30$	$5$
$5$	$2$	$2^1,3^1$	$10$	$20$	$10$
…
$5$	$5$	$1^5$	$120$	$1$	$1$

►

…

7: 24.2 Definitions and Generating Functions

… ►

Table 24.2.1: Bernoulli and Euler numbers.

► ►►►

$n$	$B_n$	$E_n$
…
$4$	$-\frac{1}{30}$	$5$
…

►

… ►

Table 24.2.3: Bernoulli numbers $B_n=N/D$.

► ►►►

$n$	$N$	$D$	$B_n$
…
$10$	$5$	$66$	$\mathrm{7.57575\hspace{0.33em}7576}$	$\mathrm{\times 10⁻²}$
…

►

►

Table 24.2.4: Euler numbers $E_n$.

► ►►►

$n$	$E_n$
…
$4$	$5$
…

►

►

Table 24.2.5: Coefficients $b_{n,k}$ of the Bernoulli polynomials $B_n\left(x\right)={\sum }_{k=0}^n{b}_{n,k}{x}^k$.

► ►►►

	$k$
…
$5$	$0$	$-\frac{1}{6}$	$0$	$\frac{5}{3}$	$-\frac{5}{2}$	$1$
…

►

►

Table 24.2.6: Coefficients $e_{n,k}$ of the Euler polynomials $E_n\left(x\right)={\sum }_{k=0}^n{e}_{n,k}{x}^k$.

► ►►►

	$k$
…
$5$	$-\frac{1}{2}$	$0$	$\frac{5}{2}$	$0$	$-\frac{5}{2}$	$1$
…

►

8: 5 Gamma Function

Chapter 5 Gamma Function

…

9: 3.4 Differentiation

… ►

$$B_{-2}^5=\frac{1}{120}(6-10t-15t^2+20t^3-5t^4),$$

►

$$B_{-1}^5=-\frac{1}{24}(12-32t+3t^2+16t^3-5t^4),$$

►

$$B_0^5=-\frac{1}{12}(4+30t-15t^2-12t^3+5t^4),$$

►

$$B_1^5=\frac{1}{12}(12+16t-21t^2-8t^3+5t^4),$$

… ►

$$B_3^5=\frac{1}{120}(4-15t^2+5t^4).$$

…

10: Staff

… ►

Richard A. Askey, University of Wisconsin, Chaps. 1, 5, 16

… ►

Ranjan Roy, Beloit College, Beloit, Chaps. 1, 4, 5

… ►

Gerhard Wolf, University of Duisberg-Essen, Chap. 28

… ►

Simon Ruijsenaars, University of Leeds, for Chaps. 5, 28

…