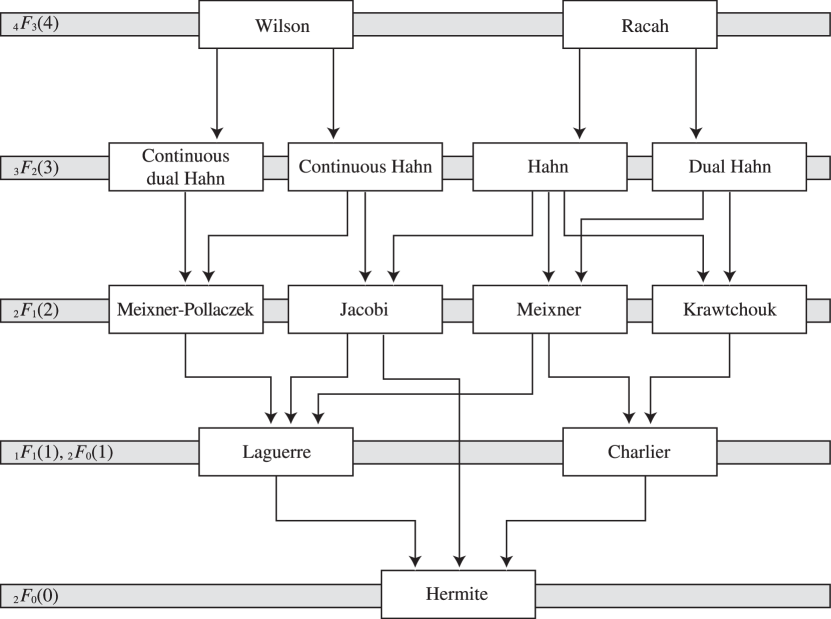
Wilson class orthogonal polynomials

SearchAdvancedHelp

(0.008 seconds)

1—10 of 16 matching pages

1: 18.25 Wilson Class: Definitions

§18.25 Wilson Class: Definitions

… ►

Table 18.25.1: Wilson class OP’s: transformations of variable, orthogonality ranges, and parameter constraints.

► ►►

OP	$p_n(x)$	$x=\lambda (y)$	Orthogonality range for $y$	Constraints
…

►

… ►

§18.25(ii) Weights and Standardizations: Continuous Cases

… ►

18.25.15 $$h_n=\frac{n!(N-n)!{\left(\gamma +\delta +2\right)}_N}{N!{\left(\gamma +1\right)}_n{\left(\delta +1\right)}_{N-n}}.$$

ⓘ

Symbols:

${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $!$: factorial (as in $n!$), $N$: positive integer, $\delta$: arbitrary small positive constant, $n$: nonnegative integer and $h_n$

Referenced by:

§18.25(iii)

Permalink:

http://dlmf.nist.gov/18.25.E15

Encodings:

pMML, png, TeX

See also:

Annotations for §18.25(iii), §18.25(iii), §18.25 and Ch.18

… ►

Table 18.25.2: Wilson class OP’s: leading coefficients.

► ►►

$p_n(x)$	$k_n$
…

►

2: 18.26 Wilson Class: Continued

… ►

§18.26(i) Representations as Generalized Hypergeometric Functions and Dualities

… ►

§18.26(ii) Limit Relations

… ►

§18.26(iii) Difference Relations

… ►

§18.26(iv) Generating Functions

… ►

§18.26(v) Asymptotic Approximations

…

3: 18.21 Hahn Class: Interrelations

… ►

§18.21(i) Dualities

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

4: 18.1 Notation

… ►

$${(z_1,\mathrm{\dots },z_k;q)}_{\mathrm{\infty }}={(z_1;q)}_{\mathrm{\infty }}\mathrm{\cdots }{(z_k;q)}_{\mathrm{\infty }}.$$

… ►

Wilson Class OP’s

…

5: 18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

§18.29 Asymptotic Approximations for $q$-Hahn and Askey–Wilson Classes

…

6: 18.28 Askey–Wilson Class

§18.28 Askey–Wilson Class

… ► … ►

§18.28(ii) Askey–Wilson Polynomials

… ►

§18.28(x) Limit Relations

… ►Genest et al. (2016) showed that these polynomials coincide with the nonsymmetric Wilson polynomials in Groenevelt (2007).

7: 18.38 Mathematical Applications

… ► …

8: Bibliography Z

… ►

Doron Zeilberger’s Maple Packages and Programs Department of Mathematics, Rutgers University, New Jersey.

ⓘ

Notes:

Includes hypergeometric and $q$-hypergeometric summation, solution of difference equations (for example, by Petkovšek’s algorithm), combinatorial algorithms, and (package LUC) evaluation of zonal polynomials.

External Links:

Home Page

Referenced by:

§ ‣ Software Cross Index, § ‣ Software Cross Index, L. Lapointe and L. Vinet (1996).

Encodings:

BibTeX

… ►

Weighted derangements and the linearization coefficients of orthogonal Sheffer polynomials. Proc. London Math. Soc. (3) 65 (1), pp. 1–22.

ⓘ

External Links:

ISSN 0024-6115, Document, Link, MathReview (R. A. Askey), ZentralBlatt

Referenced by:

§18.18(v).

Encodings:

BibTeX

… ►

“Hidden symmetry” of Askey-Wilson polynomials. Theoret. and Math. Phys. 89 (2), pp. 1146–1157.

ⓘ

External Links:

MathReview (Vadim B. Kuznetsov), ZentralBlatt

Referenced by:

§18.38(iii).

Encodings:

BibTeX

►

On some classes of polynomials orthogonal on arcs of the unit circle connected with symmetric orthogonal polynomials on an interval. J. Approx. Theory 94 (1), pp. 73–106.

ⓘ

External Links:

ISSN 0021-9045, Link, MathReview (T. S. Chihara), ZentralBlatt

Referenced by:

§18.33(iii).

Encodings:

BibTeX

…

9: 18.27 $q$-Hahn Class

§18.27 $q$-Hahn Class

… ►All these systems of OP’s have orthogonality properties of the form … ►

From Big $q$-Jacobi to Jacobi

… ►

From Big $q$-Jacobi to Little $q$-Jacobi

… ►

Limit Relations

…

10: 18.22 Hahn Class: Recurrence Relations and Differences

§18.22 Hahn Class: Recurrence Relations and Differences

►

§18.22(i) Recurrence Relations in $n$

… ►These polynomials satisfy (18.22.2) with $p_n(x)$, $A_n$, and $C_n$ as in Table 18.22.1. … ►

§18.22(ii) Difference Equations in $x$

… ►

§18.22(iii) $x$-Differences

…