Coulomb%20phase%20shift

SearchAdvancedHelp

(0.002 seconds)

11—20 of 385 matching pages

11: 33.6 Power-Series Expansions in $\rho$

§33.6 Power-Series Expansions in $\rho$

►

33.6.1 $$F_{\mathrm{\ell }}(\eta ,\rho )=C_{\mathrm{\ell }}\left(\eta \right)\sum _{k=\mathrm{\ell }+1}^{\mathrm{\infty }}{A}_k^{\mathrm{\ell }}(\eta ){\rho }^k,$$

ⓘ

Symbols:

$C_{\mathrm{\ell }}\left(\eta \right)$: normalizing constant for Coulomb radial functions, $F_{\mathrm{\ell }}(\eta ,\rho )$: regular Coulomb radial function, $k$: nonnegative integer, $\mathrm{\ell }$: nonnegative integer, $\rho$: nonnegative real variable, $\eta$: real parameter and $A_{\mathrm{\ell }+1}^{\mathrm{\ell }}$: coefficient

A&S Ref:

14.1.4, 14.1.5

Referenced by:

§33.6

Permalink:

http://dlmf.nist.gov/33.6.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §33.6 and Ch.33

►

33.6.2 $$F_{\mathrm{\ell }}^{\prime }(\eta ,\rho )=C_{\mathrm{\ell }}\left(\eta \right)\sum _{k=\mathrm{\ell }+1}^{\mathrm{\infty }}k{A}_k^{\mathrm{\ell }}(\eta ){\rho }^{k-1},$$

ⓘ

Symbols:

$C_{\mathrm{\ell }}\left(\eta \right)$: normalizing constant for Coulomb radial functions, $F_{\mathrm{\ell }}(\eta ,\rho )$: regular Coulomb radial function, $k$: nonnegative integer, $\mathrm{\ell }$: nonnegative integer, $\rho$: nonnegative real variable, $\eta$: real parameter and $A_{\mathrm{\ell }+1}^{\mathrm{\ell }}$: coefficient

A&S Ref:

14.1.4, 14.1.5

Referenced by:

§33.6

Permalink:

http://dlmf.nist.gov/33.6.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §33.6 and Ch.33

… ►

33.6.5 $$H_{\mathrm{\ell }}^{\pm }(\eta ,\rho )=\frac{{\mathrm{e}}^{\pm \mathrm{i}{\theta }_{\mathrm{\ell }}(\eta ,\rho )}}{(2\mathrm{\ell }+1)!\mathrm{\Gamma }\left(-\mathrm{\ell }\pm \mathrm{i}\eta \right)}\left(\sum _{k=0}^{\mathrm{\infty }}\frac{{\left(a\right)}_k}{{\left(2\mathrm{\ell }+2\right)}_{k}k!}{(\mp 2\mathrm{i}\rho )}^{a+k}\left(\ln \left(\mp 2\mathrm{i}\rho \right)+\psi \left(a+k\right)-\psi \left(1+k\right)-\psi \left(2\mathrm{\ell }+2+k\right)\right)-\sum _{k=1}^{2\mathrm{\ell }+1}\frac{(2\mathrm{\ell }+1)!(k-1)!}{(2\mathrm{\ell }+1-k)!{\left(1-a\right)}_k}{(\mp 2\mathrm{i}\rho )}^{a-k}\right),$$

ⓘ

Symbols:

${\theta }_{\mathrm{\ell }}(\eta ,\rho )$: phase of Coulomb functions, $\mathrm{\Gamma }\left(z\right)$: gamma function, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\psi \left(z\right)$: psi (or digamma) function, $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, $H_{\mathrm{\ell }}^{\pm }(\eta ,\rho )$: irregular Coulomb radial functions, $\ln z$: principal branch of logarithm function, $k$: nonnegative integer, $\mathrm{\ell }$: nonnegative integer, $\rho$: nonnegative real variable, $\eta$: real parameter and $a$: variable

A&S Ref:

14.1.14 (equivalent)

Referenced by:

§33.13, §33.6, §33.6, Erratum (V1.0.19) for Equation (33.6.5)

Permalink:

http://dlmf.nist.gov/33.6.E5

Encodings:

pMML, png, TeX

Errata (effective with 1.0.19):

On the right-hand side the factor in the denominator was incorrectly written as $\mathrm{\Gamma }\left(-\mathrm{\ell }+\mathrm{i}\eta \right)$. This has been corrected to $\mathrm{\Gamma }\left(-\mathrm{\ell }\pm \mathrm{i}\eta \right)$.

Reported 2018-05-15 by Ian Thompson

See also:

Annotations for §33.6 and Ch.33

… ►Corresponding expansions for $H_{\mathrm{\ell }}^{\pm }{}_{}{}^{\prime }(\eta ,\rho )$ can be obtained by combining (33.6.5) with (33.4.3) or (33.4.4).

12: 20 Theta Functions

Chapter 20 Theta Functions

…

13: 33.17 Recurrence Relations and Derivatives

§33.17 Recurrence Relations and Derivatives

►

33.17.1 $$(\mathrm{\ell }+1)rf(ϵ,\mathrm{\ell }-1;r)-(2\mathrm{\ell }+1)\left(\mathrm{\ell }(\mathrm{\ell }+1)-r\right)f(ϵ,\mathrm{\ell };r)+\mathrm{\ell }\left(1+{(\mathrm{\ell }+1)}^2ϵ\right)rf(ϵ,\mathrm{\ell }+1;r)=0,$$

ⓘ

Symbols:

$f(ϵ,\mathrm{\ell };r)$: regular Coulomb function, $\mathrm{\ell }$: nonnegative integer, $r$: real variable and $ϵ$: real parameter

Permalink:

http://dlmf.nist.gov/33.17.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §33.17 and Ch.33

►

33.17.2 $$(\mathrm{\ell }+1)\left(1+{\mathrm{\ell }}^2ϵ\right)rh(ϵ,\mathrm{\ell }-1;r)-(2\mathrm{\ell }+1)\left(\mathrm{\ell }(\mathrm{\ell }+1)-r\right)h(ϵ,\mathrm{\ell };r)+\mathrm{\ell }rh(ϵ,\mathrm{\ell }+1;r)=0,$$

ⓘ

Symbols:

$h(ϵ,\mathrm{\ell };r)$: irregular Coulomb function, $\mathrm{\ell }$: nonnegative integer, $r$: real variable and $ϵ$: real parameter

Permalink:

http://dlmf.nist.gov/33.17.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §33.17 and Ch.33

►

33.17.3 $$(\mathrm{\ell }+1)r{f}^{\prime }(ϵ,\mathrm{\ell };r)=\left({(\mathrm{\ell }+1)}^2-r\right)f(ϵ,\mathrm{\ell };r)-\left(1+{(\mathrm{\ell }+1)}^2ϵ\right)rf(ϵ,\mathrm{\ell }+1;r),$$

ⓘ

Symbols:

$f(ϵ,\mathrm{\ell };r)$: regular Coulomb function, $\mathrm{\ell }$: nonnegative integer, $r$: real variable and $ϵ$: real parameter

Permalink:

http://dlmf.nist.gov/33.17.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §33.17 and Ch.33

►

33.17.4 $$(\mathrm{\ell }+1)r{h}^{\prime }(ϵ,\mathrm{\ell };r)=\left({(\mathrm{\ell }+1)}^2-r\right)h(ϵ,\mathrm{\ell };r)-rh(ϵ,\mathrm{\ell }+1;r).$$

ⓘ

Symbols:

$h(ϵ,\mathrm{\ell };r)$: irregular Coulomb function, $\mathrm{\ell }$: nonnegative integer, $r$: real variable and $ϵ$: real parameter

Permalink:

http://dlmf.nist.gov/33.17.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §33.17 and Ch.33

14: 33.15 Graphics

§33.15 Graphics

►

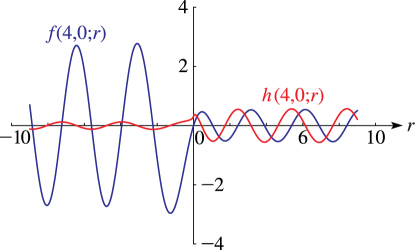
§33.15(i) Line Graphs of the Coulomb Functions $f(ϵ,\mathrm{\ell };r)$ and $h(ϵ,\mathrm{\ell };r)$

►

►►

Figure 33.15.1: $f(ϵ,\mathrm{\ell };r),h(ϵ,\mathrm{\ell };r)$ with $\mathrm{\ell }=0,ϵ=4$. Magnify

… ►

§33.15(ii) Surfaces of the Coulomb Functions $f(ϵ,\mathrm{\ell };r)$, $h(ϵ,\mathrm{\ell };r)$, $s(ϵ,\mathrm{\ell };r)$, and $c(ϵ,\mathrm{\ell };r)$

… ►

►

►

Figure 33.15.9: $h(ϵ,\mathrm{\ell };r)$ with . Magnify 3D Help

…

15: 18.39 Applications in the Physical Sciences

… ►

The Quantum Coulomb Problem

… ►This is Coulomb’s Law. … ►Derivations of (18.39.42) appear in Bethe and Salpeter (1957, pp. 12–20), and Pauling and Wilson (1985, Chapter V and Appendix VII), where the derivations are based on (18.39.36), and is also the notation of Piela (2014, §4.7), typifying the common use of the associated Coulomb–Laguerre polynomials in theoretical quantum chemistry. … ►

The Relativistic Quantum Coulomb Problem

… ►

The Coulomb–Pollaczek Polynomials

…

16: 33.18 Limiting Forms for Large $\mathrm{\ell }$

§33.18 Limiting Forms for Large $\mathrm{\ell }$

… ►

$f(ϵ,\mathrm{\ell };r)\sim {\displaystyle \frac{{(2r)}^{\mathrm{\ell }+1}}{(2\mathrm{\ell }+1)!}},$

►

$h(ϵ,\mathrm{\ell };r)\sim {\displaystyle \frac{(2\mathrm{\ell })!}{\pi {(2r)}^{\mathrm{\ell }}}}.$

17: Bibliography C

… ►

Asymptotic estimates for generalized Stirling numbers. Analysis (Munich) 20 (1), pp. 1–13.

ⓘ

External Links:

ISSN 0174-4747, MathReview (F. T. Howard), ZentralBlatt

Referenced by:

§26.8(vii).

Encodings:

BibTeX

… ►

Coulomb phase shift. American Journal of Physics 47 (8), pp. 683–684.

ⓘ

External Links:

Document

Referenced by:

§5.20.

Encodings:

BibTeX

… ►

Chebyshev approximations for the Coulomb phase shift. Math. Comp. 24 (111), pp. 671–677.

ⓘ

Notes:

Corrigendum: same journal, 26(1972), p. 1031.

External Links:

FullText, MathReview, ZentralBlatt

Referenced by:

§33.25.

Encodings:

BibTeX

… ►

Validated computation of certain hypergeometric functions. ACM Trans. Math. Software 38 (2), pp. Art. 11, 20.

ⓘ

External Links:

ISSN 0098-3500, Document, FullText, MathReview Entry, ZentralBlatt

Referenced by:

§13.29(v), §15.19(v).

Encodings:

BibTeX

… ►

Coulomb effects in the Klein-Gordon equation for pions. Phys. Rev. C 20 (2), pp. 696–704.

ⓘ

External Links:

Document

Referenced by:

5th item.

Encodings:

BibTeX

…

18: 33.1 Special Notation

… ►The main functions treated in this chapter are first the Coulomb radial functions $F_{\mathrm{\ell }}(\eta ,\rho )$, $G_{\mathrm{\ell }}(\eta ,\rho )$, $H_{\mathrm{\ell }}^{\pm }(\eta ,\rho )$ (Sommerfeld (1928)), which are used in the case of repulsive Coulomb interactions, and secondly the functions $f(ϵ,\mathrm{\ell };r)$, $h(ϵ,\mathrm{\ell };r)$, $s(ϵ,\mathrm{\ell };r)$, $c(ϵ,\mathrm{\ell };r)$ (Seaton (1982, 2002a)), which are used in the case of attractive Coulomb interactions. … ►

$P_{\mathrm{\ell }}(ϵ,r)=(2\mathrm{\ell }+1)!f(ϵ,\mathrm{\ell };r)/2^{\mathrm{\ell }+1}$, $Q_{\mathrm{\ell }}(ϵ,r)=-(2\mathrm{\ell }+1)!h(ϵ,\mathrm{\ell };r)/(2^{\mathrm{\ell }+1}A(ϵ,\mathrm{\ell }))$.

►

$f^{(0)}(ϵ,\mathrm{\ell };r)=f(ϵ,\mathrm{\ell };r)$, $f(ϵ,\mathrm{\ell };r)=s(ϵ,\mathrm{\ell };r)$, $g(ϵ,\mathrm{\ell };r)=c(ϵ,\mathrm{\ell };r)$.

19: Bibliography B

… ►

Pionic atoms. Annual Review of Nuclear and Particle Science 20, pp. 467–508.

ⓘ

External Links:

Document

Referenced by:

§33.22(iv).

Encodings:

BibTeX

… ►

A program for computing the Riemann zeta function for complex argument. Comput. Phys. Comm. 20 (3), pp. 441–445.

ⓘ

Notes:

Double-precision Fortran, maximum accuracy 10S.

External Links:

Document, Code, ZentralBlatt

Referenced by:

1st item.

Encodings:

BibTeX

… ►

Coulomb functions (negative energies). Comput. Phys. Comm. 20 (3), pp. 447–458.

ⓘ

Notes:

Double-precision Fortran code.

External Links:

Document, Code

Referenced by:

1st item, 4th item.

Encodings:

BibTeX

… ►

Some solutions of the problem of forced convection. Philos. Mag. Series 7 20, pp. 322–343.

ⓘ

External Links:

Document, ZentralBlatt

Referenced by:

§10.73(iv).

Encodings:

BibTeX

… ►

Bessel functions and modular relations of higher type and hyperbolic differential equations. Comm. Sém. Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.] 1952 (Tome Supplementaire), pp. 12–20.

ⓘ

External Links:

MathReview (S. C. van Veen), ZentralBlatt

Referenced by:

§35.5(i).

Encodings:

BibTeX

…

20: 33.14 Definitions and Basic Properties

… ►

§33.14(i) Coulomb Wave Equation

… ►

§33.14(ii) Regular Solution $f(ϵ,\mathrm{\ell };r)$

… ►

§33.14(iii) Irregular Solution $h(ϵ,\mathrm{\ell };r)$

… ►

§33.14(iv) Solutions $s(ϵ,\mathrm{\ell };r)$ and $c(ϵ,\mathrm{\ell };r)$

… ►

§33.14(v) Wronskians

…