Chebyshev

SearchAdvancedHelp

(0.001 seconds)

21—30 of 52 matching pages

21: 18.13 Continued Fractions

… ►

Chebyshev

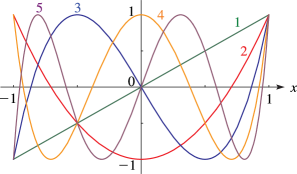
► $T_n\left(x\right)$ is the denominator of the $n$th approximant to: …and $U_n\left(x\right)$ is the denominator of the $n$th approximant to: …

22: 18.4 Graphics

… ►

►►

Figure 18.4.3: Chebyshev polynomials $T_n\left(x\right)$, $n=1,2,3,4,5$. Magnify

…

23: 18.8 Differential Equations

… ►

Table 18.8.1: Classical OP’s: differential equations $A(x)f^{\prime \prime }(x)+B(x)f^{\prime }(x)+C(x)f(x)+{\lambda }_{n}f(x)=0$.

► ►►►►

#	$f(x)$	$A(x)$	$B(x)$	$C(x)$	${\lambda }_n$
…
5	$T_n\left(x\right)$	$1-x^2$	$-x$	$0$	$n^2$
6	$U_n\left(x\right)$	$1-x^2$	$-3x$	$0$	$n(n+2)$
…

►

…

24: 13.31 Approximations

… ►

§13.31(i) Chebyshev-Series Expansions

►Luke (1969b, pp. 35 and 25) provides Chebyshev-series expansions of $M(a,b,x)$ and $U(a,b,x)$ that include the intervals $0\le x\le \alpha$ and , respectively, where $\alpha$ is an arbitrary positive constant. …

25: 18.12 Generating Functions

… ►The $z$-radii of convergence will depend on $x$, and in first instance we will assume $x\in [-1,1]$ for Jacobi, ultraspherical, Chebyshev and Legendre, $x\in [0,\mathrm{\infty })$ for Laguerre, and $x\in ℝ$ for Hermite. … ►

Chebyshev

►

18.12.7 $$\frac{1-z^2}{1-2xz+z^2}=1+2\sum _{n=1}^{\mathrm{\infty }}{T}_n\left(x\right)z^n,$$ .

ⓘ

Symbols:

$T_n\left(x\right)$: Chebyshev polynomial of the first kind, $z$: complex variable, $n$: nonnegative integer and $x$: real variable

Referenced by:

§18.12

Permalink:

http://dlmf.nist.gov/18.12.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §18.12, §18.12 and Ch.18

►

18.12.8 $$\frac{1-xz}{1-2xz+z^2}=\sum _{n=0}^{\mathrm{\infty }}{T}_n\left(x\right)z^n,$$ .

ⓘ

Symbols:

$T_n\left(x\right)$: Chebyshev polynomial of the first kind, $z$: complex variable, $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.9.6

Referenced by:

§18.12

Permalink:

http://dlmf.nist.gov/18.12.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §18.12, §18.12 and Ch.18

►

18.12.9 $$-\ln \left(1-2xz+z^2\right)=2\sum _{n=1}^{\mathrm{\infty }}\frac{T_n\left(x\right)}{n}{z}^n,$$ .

ⓘ

Symbols:

$T_n\left(x\right)$: Chebyshev polynomial of the first kind, $\ln z$: principal branch of logarithm function, $z$: complex variable, $n$: nonnegative integer and $x$: real variable

A&S Ref:

22.9.8

Referenced by:

§18.12

Permalink:

http://dlmf.nist.gov/18.12.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §18.12, §18.12 and Ch.18

…

26: 18.18 Sums

… ►

Chebyshev

… ►

Chebyshev

►

18.18.21 $$T_m\left(x\right)T_n\left(x\right)=\frac{1}{2}(T_{m+n}\left(x\right)+T_{m-n}\left(x\right)).$$

ⓘ

Symbols:

$T_n\left(x\right)$: Chebyshev polynomial of the first kind, $m$: nonnegative integer, $n$: nonnegative integer and $x$: real variable

Permalink:

http://dlmf.nist.gov/18.18.E21

Encodings:

pMML, png, TeX

See also:

Annotations for §18.18(v), §18.18(v), §18.18 and Ch.18

… ►

Chebyshev

… ►

Legendre and Chebyshev

…

27: 19.38 Approximations

… ►Cody (1965b) gives Chebyshev-series expansions (§3.11(ii)) with maximum precision 25D. …

28: 18.38 Mathematical Applications

… ►

§18.38(i) Classical OP’s: Numerical Analysis

►

Approximation Theory

►The monic Chebyshev polynomial $2^{1-n}{T}_n\left(x\right)$, $n\ge 1$, enjoys the ‘minimax’ property on the interval $[-1,1]$, that is, $|2^{1-n}{T}_n\left(x\right)|$ has the least maximum value among all monic polynomials of degree $n$. … ►

Differential Equations: Spectral Methods

►Linear ordinary differential equations can be solved directly in series of Chebyshev polynomials (or other OP’s) by a method originated by Clenshaw (1957). …

29: Bibliography C

… ►

Sur la fonction qui détermine la totalité des nombres premiers inférieurs à une limite donnée. Mem. Ac. Sc. St. Pétersbourg 6, pp. 141–157.

ⓘ

Referenced by:

§25.16(i).

Encodings:

BibTeX

… ►

A note on the summation of Chebyshev series. Math. Tables Aids Comput. 9 (51), pp. 118–120.

ⓘ

External Links:

FullText, MathReview, ZentralBlatt

Referenced by:

§18.40(i).

Encodings:

BibTeX

… ►

Chebyshev polynomial expansions of complete elliptic integrals. Math. Comp. 19 (90), pp. 249–259.

ⓘ

External Links:

FullText, MathReview, ZentralBlatt

Referenced by:

§19.38.

Encodings:

BibTeX

►

Chebyshev approximations for the Fresnel integrals. Math. Comp. 22 (102), pp. 450–453.

ⓘ

Notes:

with Microfiche Supplement

External Links:

FullText, MathReview, ZentralBlatt

Referenced by:

3rd item.

Encodings:

BibTeX

►

Rational Chebyshev approximations for the error function. Math. Comp. 23 (107), pp. 631–637.

ⓘ

External Links:

FullText, MathReview, ZentralBlatt

Referenced by:

2nd item.

Encodings:

BibTeX

…

30: Bibliography R

… ►

Rational Chebyshev approximation by Remes’ algorithms. Numer. Math. 7 (4), pp. 322–330.

ⓘ

External Links:

ISSN 0029-599X, Document, MathReview (C. W. Clenshaw), ZentralBlatt

Referenced by:

§3.11(i).

Encodings:

BibTeX

… ►

High precision Chebyshev expansions for Airy functions and their derivatives. Technical report University of Birmingham Computer Centre.

ⓘ

Referenced by:

3rd item.

Encodings:

BibTeX

►

Remark on Algorithm 498: Airy functions using Chebyshev series approximations. ACM Trans. Math. Software 7 (3), pp. 404–405.

ⓘ

External Links:

ISSN 0098-3500, Document

Referenced by:

1st item.

Encodings:

BibTeX

… ►

General Computation Methods of Chebyshev Approximation. The Problems with Linear Real Parameters. Publishing House of the Academy of Science of the Ukrainian SSR, Kiev.

ⓘ

Notes:

English translation, AEC-TR-4491, United States Atomic Energy Commission

External Links:

MathReview (A. S. Householder)

Referenced by:

§3.11(iii).

Encodings:

BibTeX

… ►

On Simple Waves with Profiles in the form of some Special Functions—Chebyshev-Hermite, Mathieu, Whittaker—in Two-phase Media. In Differential Operators and Related Topics, Vol. I (Odessa, 1997), Operator Theory: Advances and Applications, Vol. 117, pp. 313–322.

ⓘ

External Links:

ISBN 3-7643-6287-1, MathReview Entry, ZentralBlatt

Referenced by:

5th item.

Encodings:

BibTeX

…