Bessel functions and spherical Bessel functions

SearchAdvancedHelp

(0.019 seconds)

1—10 of 61 matching pages

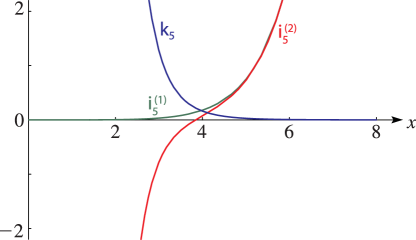
1: 10.48 Graphs

§10.48 Graphs

… ►

►►

Figure 10.48.7: ${𝗂}_5^{(1)}\left(x\right)$, ${𝗂}_5^{(2)}\left(x\right)$, ${𝗄}_5\left(x\right)$, $0\le x\le 8$. Magnify

2: 10.76 Approximations

… ►

Spherical Bessel Functions

…

3: 10.52 Limiting Forms

§10.52 Limiting Forms

… ►

10.52.1 $${𝗃}_n\left(z\right),{𝗂}_n^{(1)}\left(z\right)\sim z^n/(2n+1)!!,$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $!!$: double factorial, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.4

Permalink:

http://dlmf.nist.gov/10.52.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

►

10.52.2 $$-{𝗒}_n\left(z\right),\mathrm{i}{𝗁}_n^{(1)}\left(z\right),-\mathrm{i}{𝗁}_n^{(2)}\left(z\right),{(-1)}^n{𝗂}_n^{(2)}\left(z\right),(2/\pi ){𝗄}_n\left(z\right)\sim (2n-1)!!/z^{n+1}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!!$: double factorial, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, ${𝗁}_n^{(1)}\left(z\right)$: spherical Bessel function of the third kind, ${𝗁}_n^{(2)}\left(z\right)$: spherical Bessel function of the third kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.5

Permalink:

http://dlmf.nist.gov/10.52.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

… ►

10.52.5 $${𝗂}_n^{(1)}\left(z\right)\sim {𝗂}_n^{(2)}\left(z\right)\sim \frac{1}{2}{z}^{-1}{\mathrm{e}}^z,$$ ,

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{ph}$: phase, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $z$: complex variable and $\delta$: small positive constant

Permalink:

http://dlmf.nist.gov/10.52.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

►

10.52.6 $${𝗄}_n\left(z\right)\sim \frac{1}{2}\pi z^{-1}{\mathrm{e}}^{-z}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Permalink:

http://dlmf.nist.gov/10.52.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

4: 10.1 Special Notation

… ►The main functions treated in this chapter are the Bessel functions $J_{\nu }\left(z\right)$, $Y_{\nu }\left(z\right)$; Hankel functions $H_{\nu }^{(1)}\left(z\right)$, $H_{\nu }^{(2)}\left(z\right)$; modified Bessel functions $I_{\nu }\left(z\right)$, $K_{\nu }\left(z\right)$; spherical Bessel functions ${𝗃}_n\left(z\right)$, ${𝗒}_n\left(z\right)$, ${𝗁}_n^{(1)}\left(z\right)$, ${𝗁}_n^{(2)}\left(z\right)$; modified spherical Bessel functions ${𝗂}_n^{(1)}\left(z\right)$, ${𝗂}_n^{(2)}\left(z\right)$, ${𝗄}_n\left(z\right)$; Kelvin functions ${\mathrm{ber}}_{\nu }\left(x\right)$, ${\mathrm{bei}}_{\nu }\left(x\right)$, ${\ker }_{\nu }\left(x\right)$, ${\mathrm{kei}}_{\nu }\left(x\right)$. For the spherical Bessel functions and modified spherical Bessel functions the order $n$ is a nonnegative integer. … ►For older notations see British Association for the Advancement of Science (1937, pp. xix–xx) and Watson (1944, Chapters 1–3).

5: 10.51 Recurrence Relations and Derivatives

… ►Let $f_n(z)$ denote any of ${𝗃}_n\left(z\right)$, ${𝗒}_n\left(z\right)$, ${𝗁}_n^{(1)}\left(z\right)$, or ${𝗁}_n^{(2)}\left(z\right)$. … ►

$$n{f}_{n-1}(z)-(n+1)f_{n+1}(z)=(2n+1)f_n^{\prime }(z),$$ $n=1,2,\mathrm{\dots }$,

… ►

$$f_n^{\prime }(z)=-f_{n+1}(z)+(n/z)f_n(z),$$ $n=0,1,\mathrm{\dots }.$

… ►Then … ►

$$n{g}_{n-1}(z)+(n+1)g_{n+1}(z)=(2n+1)g_n^{\prime }(z),$$ $n=1,2,\mathrm{\dots }$,

…

6: 10.50 Wronskians and Cross-Products

§10.50 Wronskians and Cross-Products

… ►

10.50.4 $${𝗃}_0\left(z\right){𝗃}_n\left(z\right)+{𝗒}_0\left(z\right){𝗒}_n\left(z\right)=\cos \left(\frac{1}{2}n\pi \right)\sum _{k=0}^{\lfloor n/2\rfloor }{(-1)}^k\frac{a_{2k}(n+\frac{1}{2})}{z^{2k+2}}+\sin \left(\frac{1}{2}n\pi \right)\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{(-1)}^k\frac{a_{2k+1}(n+\frac{1}{2})}{z^{2k+3}},$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\lfloor x\rfloor$: floor of $x$ , $\sin z$: sine function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $a_k(\nu )$: polynomial coefficient

A&S Ref:

10.1.33 (modified)

Referenced by:

§10.50, §10.50

Permalink:

http://dlmf.nist.gov/10.50.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.50 and Ch.10

…

7: 10.47 Definitions and Basic Properties

… ► … ►

Equation (10.47.1)

… ►

Equation (10.47.2)

… ► … ►

§10.47(iv) Interrelations

…

8: 10.73 Physical Applications

… ► … ►

§10.73(ii) Spherical Bessel Functions

►The functions ${𝗃}_n\left(x\right)$, ${𝗒}_n\left(x\right)$, ${𝗁}_n^{(1)}\left(x\right)$, and ${𝗁}_n^{(2)}\left(x\right)$ arise in the solution (again by separation of variables) of the Helmholtz equation in spherical coordinates $\rho ,\theta ,\varphi$ (§1.5(ii)): …Accordingly, the spherical Bessel functions appear in all problems in three dimensions with spherical symmetry involving the scattering of electromagnetic radiation. …In quantum mechanics the spherical Bessel functions arise in the solution of the Schrödinger wave equation for a particle in a central potential. …

9: 10.49 Explicit Formulas

… ►

§10.49(i) Unmodified Functions

… ►

§10.49(ii) Modified Functions

… ►

§10.49(iii) Rayleigh’s Formulas

… ►

§10.49(iv) Sums or Differences of Squares

… ►

10.49.20 $${\left({𝗂}_n^{(1)}\left(z\right)\right)}^2-{\left({𝗂}_n^{(2)}\left(z\right)\right)}^2={(-1)}^{n+1}\sum _{k=0}^n{(-1)}^k\frac{s_k(n+\frac{1}{2})}{z^{2k+2}}.$$

ⓘ

Symbols:

${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer, $z$: complex variable and $s_k(n)$

A&S Ref:

10.2.26

Referenced by:

§10.49(iv)

Permalink:

http://dlmf.nist.gov/10.49.E20

Encodings:

pMML, png, TeX

See also:

Annotations for §10.49(iv), §10.49 and Ch.10

…

10: 10.55 Continued Fractions

§10.55 Continued Fractions

…