§29.4 Graphics

Permalink:: http://dlmf.nist.gov/29.4

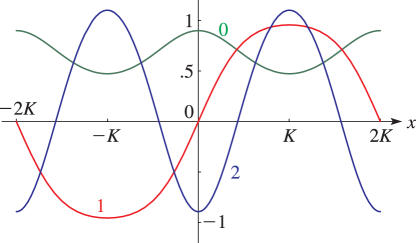
§29.4(i) Eigenvalues of Lamé’s Equation: Line Graphs
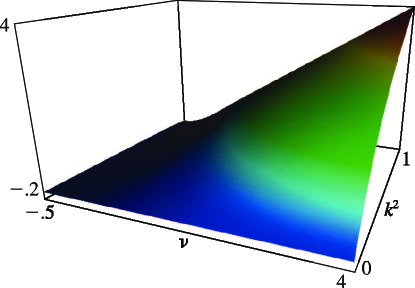
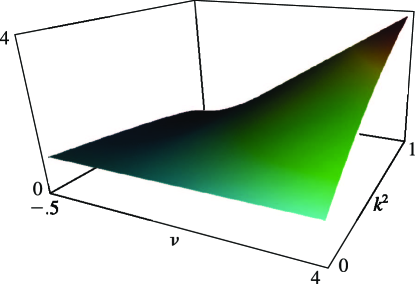
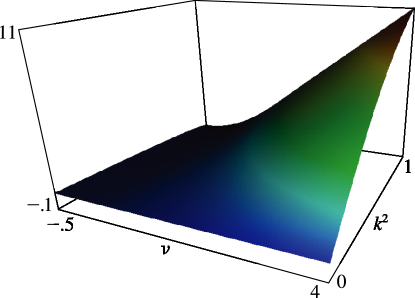
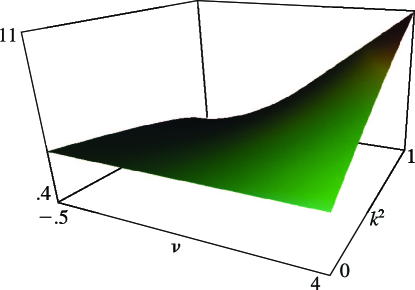
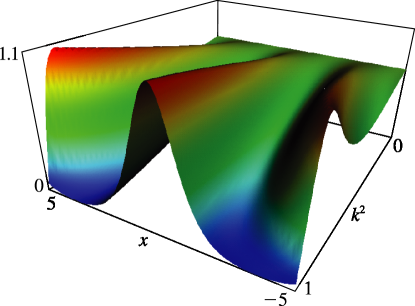
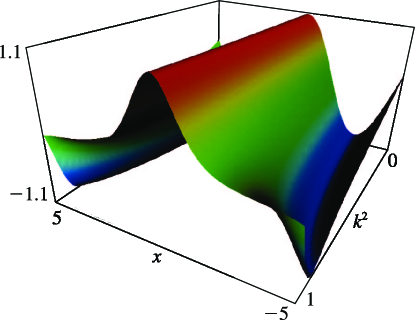
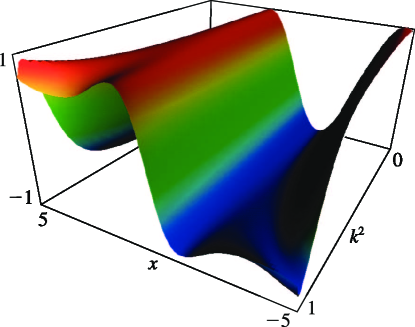
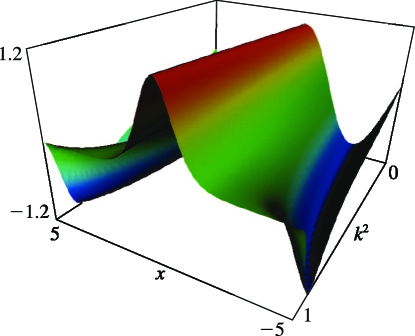
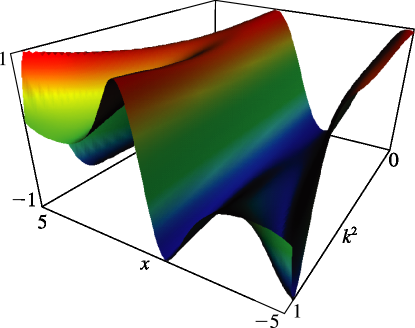
§29.4(ii) Eigenvalues of Lamé’s Equation: Surfaces
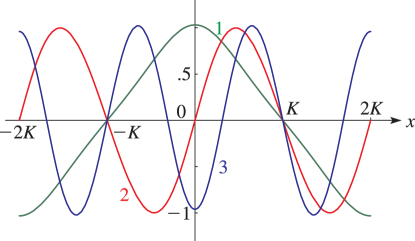
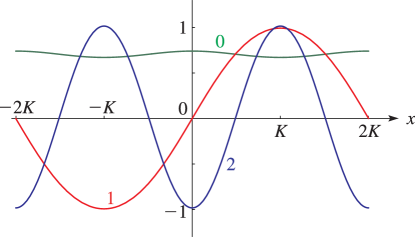
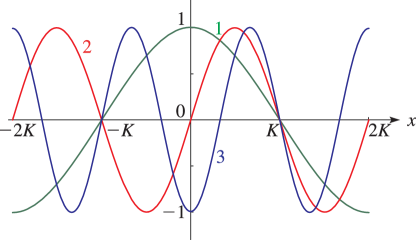
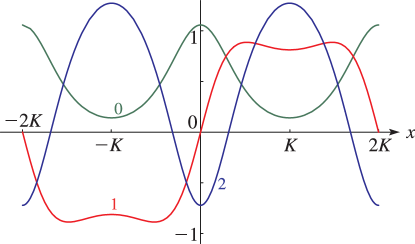
§29.4(iii) Lamé Functions: Line Graphs
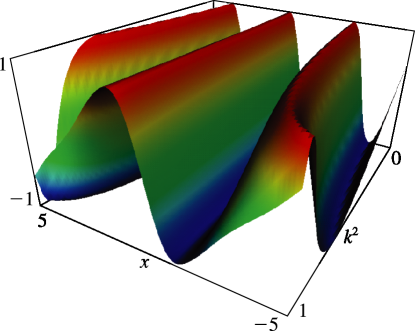
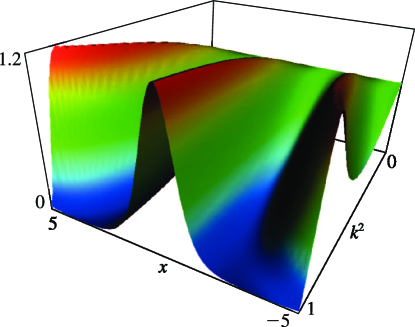
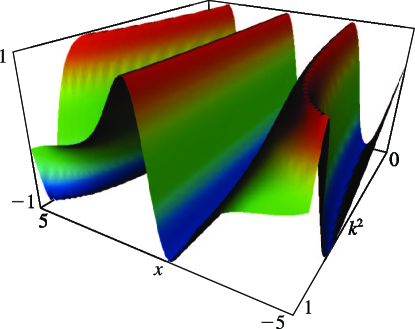
§29.4(iv) Lamé Functions: Surfaces

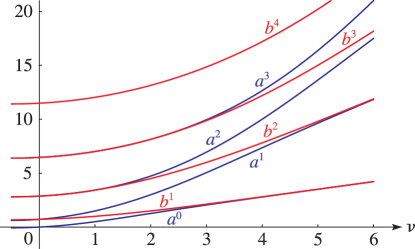
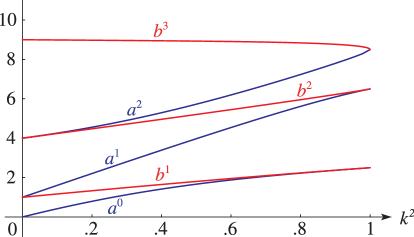
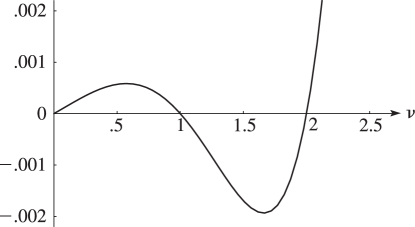
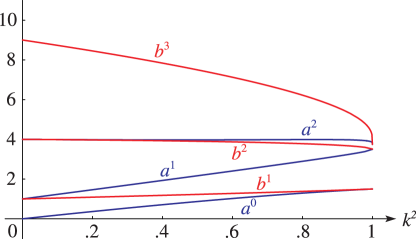
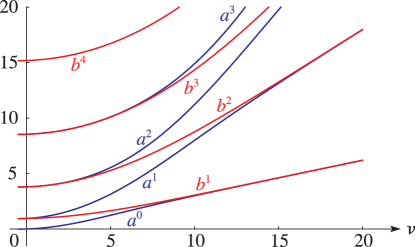
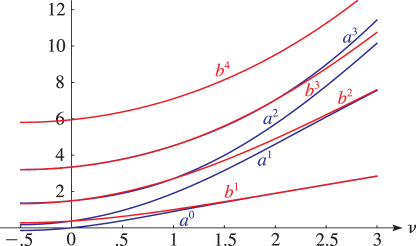
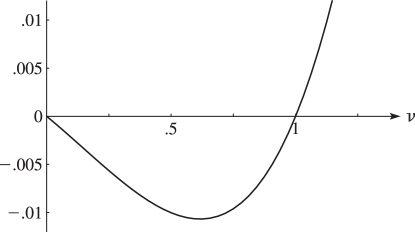
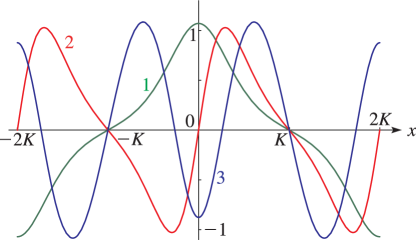
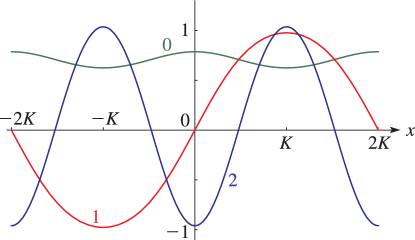
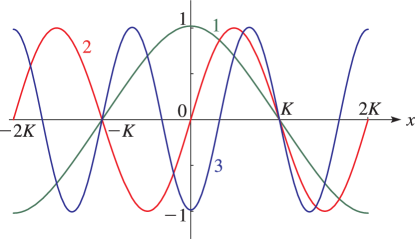
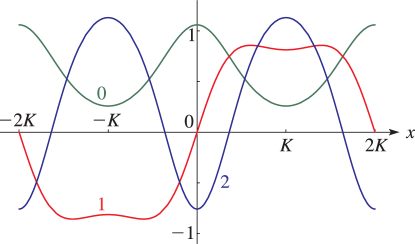
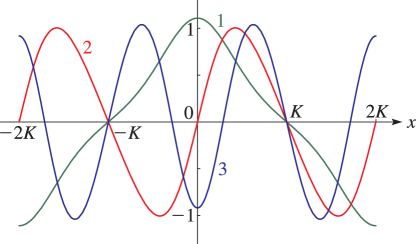
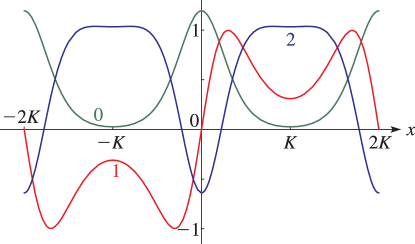
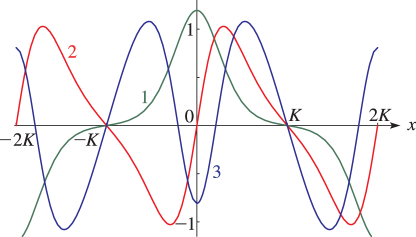
§29.4(i) Eigenvalues of Lamé’s Equation: Line Graphs

Notes:: These graphs were produced at NIST.
Keywords:: Lamé functions
Permalink:: http://dlmf.nist.gov/29.4.i

Figure 29.4.1: $\mathop{a^{{m}}_{{\nu}}\/}\nolimits\!\left(0.5\right)$ , $\mathop{b^{{m+1}}_{{\nu}}\/}\nolimits\!\left(0.5\right)$ as functions of $\nu$ for $m=0,1,2,3$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $m$ : nonnegative integer and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F1
Encodings:: pdf, png

Figure 29.4.2: $\mathop{a^{{3}}_{{\nu}}\/}\nolimits\!\left(0.5\right)-\mathop{b^{{3}}_{{\nu}}\/}\nolimits\!\left(0.5\right)$ as a function of $\nu$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F2
Encodings:: pdf, png

Figure 29.4.3: $\mathop{a^{{m}}_{{1.5}}\/}\nolimits\!\left(k^{2}\right)$ , $\mathop{b^{{m+1}}_{{1.5}}\/}\nolimits\!\left(k^{2}\right)$ as functions of $k^{2}$ for $m=0,1,2$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $m$ : nonnegative integer and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F3
Encodings:: pdf, png

Figure 29.4.4: $\mathop{a^{{m}}_{{\nu}}\/}\nolimits\!\left(0.1\right)$ , $\mathop{b^{{m+1}}_{{\nu}}\/}\nolimits\!\left(0.1\right)$ as functions of $\nu$ for $m=0,1,2,3$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $m$ : nonnegative integer and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F4
Encodings:: pdf, png

Figure 29.4.5: $\mathop{a^{{m}}_{{\nu}}\/}\nolimits\!\left(0.9\right)$ , $\mathop{b^{{m+1}}_{{\nu}}\/}\nolimits\!\left(0.9\right)$ as functions of $\nu$ for $m=0,1,2,3$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $m$ : nonnegative integer and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F5
Encodings:: pdf, png

Figure 29.4.6: $\mathop{a^{{2}}_{{\nu}}\/}\nolimits\!\left(0.5\right)-\mathop{b^{{2}}_{{\nu}}\/}\nolimits\!\left(0.5\right)$ as a function of $\nu$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F6
Encodings:: pdf, png

Figure 29.4.7: $\mathop{a^{{4}}_{{\nu}}\/}\nolimits\!\left(0.5\right)-\mathop{b^{{4}}_{{\nu}}\/}\nolimits\!\left(0.5\right)$ as a function of $\nu$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F7
Encodings:: pdf, png

Figure 29.4.8: $\mathop{a^{{m}}_{{2.5}}\/}\nolimits\!\left(k^{2}\right)$ , $\mathop{b^{{m+1}}_{{2.5}}\/}\nolimits\!\left(k^{2}\right)$ as functions of $k^{2}$ for $m=0,1,2$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $m$ : nonnegative integer and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F8
Encodings:: pdf, png

§29.4(ii) Eigenvalues of Lamé’s Equation: Surfaces

Notes:: These surfaces were produced at NIST.
Keywords:: Lamé functions
Permalink:: http://dlmf.nist.gov/29.4.ii

Visualization Help

Figure 29.4.9: $\mathop{a^{{0}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ as a function of $\nu$ and $k^{2}$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $k$ : real parameter and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F9
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 29.4.10: $\mathop{b^{{1}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ as a function of $\nu$ and $k^{2}$ .

Symbols:: $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $k$ : real parameter and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F10
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 29.4.11: $\mathop{a^{{1}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ as a function of $\nu$ and $k^{2}$ .

Symbols:: $\mathop{a^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $k$ : real parameter and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F11
Encodings:: VRML, X3D, pdf, png

Visualization Help

Figure 29.4.12: $\mathop{b^{{2}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ as a function of $\nu$ and $k^{2}$ .

Symbols:: $\mathop{b^{{n}}_{{\nu}}\/}\nolimits\!\left(k^{2}\right)$ : eigenvalues of Lamé’s equation, $k$ : real parameter and $\nu$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F12
Encodings:: VRML, X3D, pdf, png

§29.4(iii) Lamé Functions: Line Graphs

Notes:: These graphs were produced at NIST.
Keywords:: Lamé functions
Permalink:: http://dlmf.nist.gov/29.4.iii

Figure 29.4.13: $\mathop{\mathit{Ec}^{{m}}_{{1.5}}\/}\nolimits\!\left(x,0.5\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=0,1,2$ . $\!\mathop{K\/}\nolimits\!=1.85407\ldots$ .

Symbols:: $\mathop{\mathit{Ec}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F13
Encodings:: pdf, png

Figure 29.4.14: $\mathop{\mathit{Es}^{{m}}_{{1.5}}\/}\nolimits\!\left(x,0.5\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=1,2,3$ . $\!\mathop{K\/}\nolimits\!=1.85407\ldots$ .

Symbols:: $\mathop{\mathit{Es}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F14
Encodings:: pdf, png

Figure 29.4.15: $\mathop{\mathit{Ec}^{{m}}_{{1.5}}\/}\nolimits\!\left(x,0.1\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=0,1,2$ . $\!\mathop{K\/}\nolimits\!=1.61244\ldots$ .

Symbols:: $\mathop{\mathit{Ec}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F15
Encodings:: pdf, png

Figure 29.4.16: $\mathop{\mathit{Es}^{{m}}_{{1.5}}\/}\nolimits\!\left(x,0.1\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=1,2,3$ . $\!\mathop{K\/}\nolimits\!=1.61244\ldots$ .

Symbols:: $\mathop{\mathit{Es}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F16
Encodings:: pdf, png

Figure 29.4.17: $\mathop{\mathit{Ec}^{{m}}_{{1.5}}\/}\nolimits\!\left(x,0.9\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=0,1,2$ . $\!\mathop{K\/}\nolimits\!=2.57809\ldots$ .

Symbols:: $\mathop{\mathit{Ec}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F17
Encodings:: pdf, png

Figure 29.4.18: $\mathop{\mathit{Es}^{{m}}_{{1.5}}\/}\nolimits\!\left(x,0.9\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=1,2,3$ . $\!\mathop{K\/}\nolimits\!=2.57809\ldots$ .

Symbols:: $\mathop{\mathit{Es}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F18
Encodings:: pdf, png

Figure 29.4.19: $\mathop{\mathit{Ec}^{{m}}_{{2.5}}\/}\nolimits\!\left(x,0.1\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=0,1,2$ . $\!\mathop{K\/}\nolimits\!=1.61244\ldots$ .

Symbols:: $\mathop{\mathit{Ec}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F19
Encodings:: pdf, png

Figure 29.4.20: $\mathop{\mathit{Es}^{{m}}_{{2.5}}\/}\nolimits\!\left(x,0.1\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=1,2,3$ . $\!\mathop{K\/}\nolimits\!=1.61244\ldots$ .

Symbols:: $\mathop{\mathit{Es}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F20
Encodings:: pdf, png

Figure 29.4.21: $\mathop{\mathit{Ec}^{{m}}_{{2.5}}\/}\nolimits\!\left(x,0.5\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=0,1,2$ . $\!\mathop{K\/}\nolimits\!=1.85407\ldots$ .

Symbols:: $\mathop{\mathit{Ec}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F21
Encodings:: pdf, png

Figure 29.4.22: $\mathop{\mathit{Es}^{{m}}_{{2.5}}\/}\nolimits\!\left(x,0.5\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=1,2,3$ . $\!\mathop{K\/}\nolimits\!=1.85407\ldots$ .

Symbols:: $\mathop{\mathit{Es}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F22
Encodings:: pdf, png

Figure 29.4.23: $\mathop{\mathit{Ec}^{{m}}_{{2.5}}\/}\nolimits\!\left(x,0.9\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=0,1,2$ . $\!\mathop{K\/}\nolimits\!=2.57809\ldots$ .

Symbols:: $\mathop{\mathit{Ec}^{{m}}_{{\nu}}\/}\nolimits\!\left(z,k^{2}\right)$ : Lamé function, $\mathop{K\/}\nolimits\!\left(k\right)$ : Legendre’s complete elliptic integral of the first kind, $m$ : nonnegative integer, $x$ : real variable and $k$ : real parameter
Permalink:: http://dlmf.nist.gov/29.4.F23
Encodings:: pdf, png

Figure 29.4.24: $\mathop{\mathit{Es}^{{m}}_{{2.5}}\/}\nolimits\!\left(x,0.9\right)$ for $-2\!\mathop{K\/}\nolimits\!\leq x\leq 2\!\mathop{K\/}\nolimits\!$ , $m=1,2,3$ . $\!\mathop{K\/}\nolimits\!=2.57809\ldots$ .