with other orthogonal polynomials

SearchAdvancedHelp

(0.010 seconds)

1—10 of 59 matching pages

1: 16.7 Relations to Other Functions

§16.7 Relations to Other Functions

…

2: 18.21 Hahn Class: Interrelations

§18.21 Hahn Class: Interrelations

… ►

Hahn $\to$ Jacobi

… ►

Meixner $\to$ Laguerre

… ►

Charlier $\to$ Hermite

… ►

►►

Figure 18.21.1: Askey scheme. … Magnify

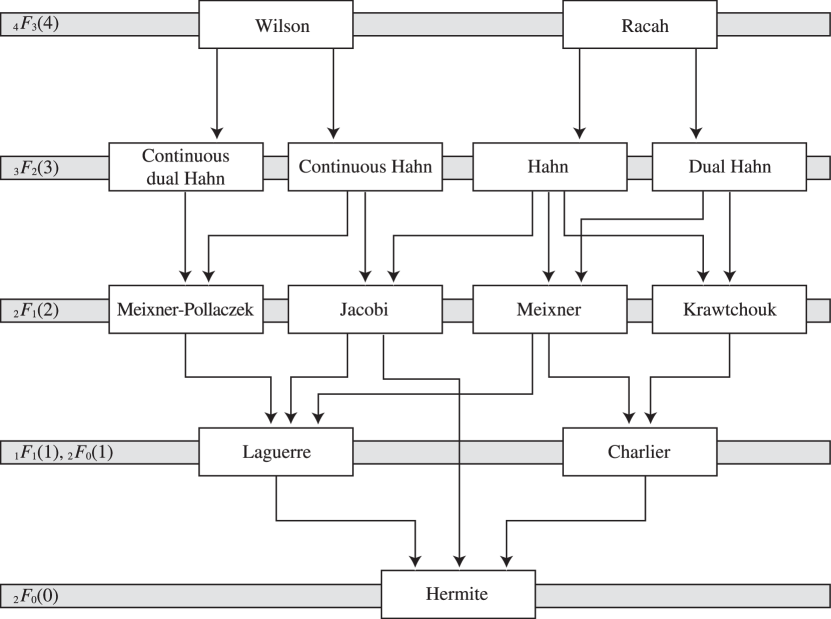3: 18.7 Interrelations and Limit Relations

§18.7 Interrelations and Limit Relations

… ►

Legendre, Ultraspherical, and Jacobi

… ►

Jacobi $\to$ Laguerre

… ►

Laguerre $\to$ Hermite

… ► See §18.11(ii) for limit formulas of Mehler–Heine type.

4: 18.26 Wilson Class: Continued

… ►

§18.26(i) Representations as Generalized Hypergeometric Functions and Dualities

… ►

§18.26(ii) Limit Relations

… ►See also Figure 18.21.1. … ►

§18.26(iv) Generating Functions

…

5: 18.11 Relations to Other Functions

… ►

Ultraspherical

…

6: 18.20 Hahn Class: Explicit Representations

… ►

§18.20(ii) Hypergeometric Function and Generalized Hypergeometric Functions

…

7: 18.5 Explicit Representations

… ►

§18.5(iii) Finite Power Series, the Hypergeometric Function, and Generalized Hypergeometric Functions

…

8: 18.37 Classical OP’s in Two or More Variables

… ►

Definition in Terms of Jacobi Polynomials

…

9: 15.9 Relations to Other Functions

… ►

§15.9(i) Orthogonal Polynomials

… ►

15.9.10 $$P_n^{(\lambda )}(x;\varphi )=\frac{{\left(2\lambda \right)}_n}{n!}{\mathrm{e}}^{n\mathrm{i}\varphi }F(\genfrac{}{}{0pt}{}{-n,\lambda +\mathrm{i}x}{2\lambda };1-{\mathrm{e}}^{-2\mathrm{i}\varphi }).$$

ⓘ

Symbols:

$F(a,b;c;z)$ or $F(\genfrac{}{}{0pt}{}{a,b}{c};z)$: $={}_2{}^{}F_1^{}(a,b;c;z)$ Gauss’ hypergeometric function, $P_n^{(\lambda )}(x;\varphi )$: Meixner–Pollaczek polynomial, ${\left(a\right)}_n$: Pochhammer’s symbol (or shifted factorial), $\mathrm{e}$: base of natural logarithm, $!$: factorial (as in $n!$), $\mathrm{i}$: imaginary unit, $x$: real variable and $n$: integer

Permalink:

http://dlmf.nist.gov/15.9.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §15.9(i), §15.9(i), §15.9 and Ch.15

…

10: 13.18 Relations to Other Functions

… ►

§13.18(v) Orthogonal Polynomials

…