trigonometric functions

SearchAdvancedHelp

(0.016 seconds)

11—20 of 339 matching pages

11: 4.15 Graphics

… ►

§4.15(i) Real Arguments

… ►

► … ►

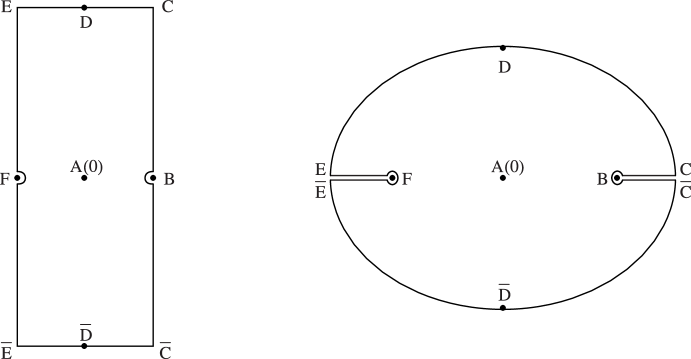
Figure 4.15.7: Conformal mapping of sine and inverse sine. … Magnify

►

§4.15(iii) Complex Arguments: Surfaces

… ►

4.15.1 $$\cos \left(x+\mathrm{i}y\right)=\sin \left(x+\frac{1}{2}\pi +\mathrm{i}y\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $x$: real variable and $y$: real variable

Permalink:

http://dlmf.nist.gov/4.15.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.15(iii), §4.15 and Ch.4

… ►The corresponding surfaces for $\arccos \left(x+\mathrm{i}y\right)$, $\mathrm{arccot}\left(x+\mathrm{i}y\right)$, $\mathrm{arcsec}\left(x+\mathrm{i}y\right)$ can be visualized from Figures 4.15.9, 4.15.11, 4.15.13 with the aid of equations (4.23.16)–(4.23.18).

12: 4.17 Special Values and Limits

… ►

Table 4.17.1: Trigonometric functions: values at multiples of $\frac{1}{12}\pi$.

► ►►

$\theta$	$\sin \theta$	$\cos \theta$	$\tan \theta$	$\csc \theta$	$\sec \theta$	$\cot \theta$
…

►

►

4.17.1 $$\underset{z\to 0}{lim}\frac{\sin z}{z}=1,$$

ⓘ

Symbols:

$\sin z$: sine function and $z$: complex variable

A&S Ref:

4.3.74

Permalink:

http://dlmf.nist.gov/4.17.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.17 and Ch.4

►

4.17.2 $$\underset{z\to 0}{lim}\frac{\tan z}{z}=1.$$

ⓘ

Symbols:

$\tan z$: tangent function and $z$: complex variable

A&S Ref:

4.3.75

Permalink:

http://dlmf.nist.gov/4.17.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.17 and Ch.4

…

13: 22.10 Maclaurin Series

… ►

22.10.4 $$\mathrm{sn}(z,k)=\sin z-\frac{k^2}{4}(z-\sin z\cos z)\cos z+O\left(k^4\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{sn}(z,k)$: Jacobian elliptic function, $\cos z$: cosine function, $\sin z$: sine function, $z$: complex and $k$: modulus

A&S Ref:

16.13.1

Referenced by:

§22.10(ii), §22.20(iii)

Permalink:

http://dlmf.nist.gov/22.10.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §22.10(ii), §22.10 and Ch.22

►

22.10.5 $$\mathrm{cn}(z,k)=\cos z+\frac{k^2}{4}(z-\sin z\cos z)\sin z+O\left(k^4\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{cn}(z,k)$: Jacobian elliptic function, $\cos z$: cosine function, $\sin z$: sine function, $z$: complex and $k$: modulus

A&S Ref:

16.13.2

Referenced by:

§22.20(iii)

Permalink:

http://dlmf.nist.gov/22.10.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §22.10(ii), §22.10 and Ch.22

… ►

22.10.7 $$\mathrm{sn}(z,k)=\tanh z-\frac{k_{}^{\prime }{}_{}{}^2}{4}(z-\sinh z\cosh z){\mathrm{sech}}^{2}z+O\left(k_{}^{\prime }{}_{}{}^4\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{sn}(z,k)$: Jacobian elliptic function, $\cosh z$: hyperbolic cosine function, $\mathrm{sech}z$: hyperbolic secant function, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $z$: complex, $k$: modulus and $k^{\prime }$: complementary modulus

A&S Ref:

16.15.1

Referenced by:

§22.10(ii)

Permalink:

http://dlmf.nist.gov/22.10.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §22.10(ii), §22.10 and Ch.22

►

22.10.8 $$\mathrm{cn}(z,k)=\mathrm{sech}z+\frac{k_{}^{\prime }{}_{}{}^2}{4}(z-\sinh z\cosh z)\tanh z\mathrm{sech}z+O\left(k_{}^{\prime }{}_{}{}^4\right),$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{cn}(z,k)$: Jacobian elliptic function, $\cosh z$: hyperbolic cosine function, $\mathrm{sech}z$: hyperbolic secant function, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $z$: complex, $k$: modulus and $k^{\prime }$: complementary modulus

A&S Ref:

16.15.2

Permalink:

http://dlmf.nist.gov/22.10.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §22.10(ii), §22.10 and Ch.22

►

22.10.9 $$\mathrm{dn}(z,k)=\mathrm{sech}z+\frac{k_{}^{\prime }{}_{}{}^2}{4}(z+\sinh z\cosh z)\tanh z\mathrm{sech}z+O\left(k_{}^{\prime }{}_{}{}^4\right).$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $\mathrm{dn}(z,k)$: Jacobian elliptic function, $\cosh z$: hyperbolic cosine function, $\mathrm{sech}z$: hyperbolic secant function, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $z$: complex, $k$: modulus and $k^{\prime }$: complementary modulus

A&S Ref:

16.15.3

Referenced by:

§22.10(ii)

Permalink:

http://dlmf.nist.gov/22.10.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §22.10(ii), §22.10 and Ch.22

…

14: 4.35 Identities

… ►

4.35.34 $$\sinh z=\sinh x\cos y+\mathrm{i}\cosh x\sin y,$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $x$: real variable, $y$: real variable and $z$: complex variable

A&S Ref:

4.5.49

Permalink:

http://dlmf.nist.gov/4.35.E34

Encodings:

pMML, png, TeX

See also:

Annotations for §4.35(iv), §4.35 and Ch.4

►

4.35.35 $$\cosh z=\cosh x\cos y+\mathrm{i}\sinh x\sin y,$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $x$: real variable, $y$: real variable and $z$: complex variable

A&S Ref:

4.5.50

Permalink:

http://dlmf.nist.gov/4.35.E35

Encodings:

pMML, png, TeX

See also:

Annotations for §4.35(iv), §4.35 and Ch.4

►

4.35.36 $$\tanh z=\frac{\sinh \left(2x\right)+\mathrm{i}\sin \left(2y\right)}{\cosh \left(2x\right)+\cos \left(2y\right)},$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\tanh z$: hyperbolic tangent function, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $x$: real variable, $y$: real variable and $z$: complex variable

A&S Ref:

4.5.51

Permalink:

http://dlmf.nist.gov/4.35.E36

Encodings:

pMML, png, TeX

See also:

Annotations for §4.35(iv), §4.35 and Ch.4

►

4.35.37 $$\coth z=\frac{\sinh \left(2x\right)-\mathrm{i}\sin \left(2y\right)}{\cosh \left(2x\right)-\cos \left(2y\right)}.$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\coth z$: hyperbolic cotangent function, $\sinh z$: hyperbolic sine function, $\mathrm{i}$: imaginary unit, $\sin z$: sine function, $x$: real variable, $y$: real variable and $z$: complex variable

A&S Ref:

4.5.52

Permalink:

http://dlmf.nist.gov/4.35.E37

Encodings:

pMML, png, TeX

See also:

Annotations for §4.35(iv), §4.35 and Ch.4

►

4.35.38 $$|\sinh z|={({\sinh }^{2}x+{\sin }^{2}y)}^{1/2}={\left(\frac{1}{2}(\cosh \left(2x\right)-\cos \left(2y\right))\right)}^{1/2},$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\sin z$: sine function, $x$: real variable, $y$: real variable and $z$: complex variable

A&S Ref:

4.5.54

Permalink:

http://dlmf.nist.gov/4.35.E38

Encodings:

pMML, png, TeX

See also:

Annotations for §4.35(iv), §4.35 and Ch.4

…

15: 4.42 Solution of Triangles

§4.42 Solution of Triangles

… ►

4.42.1 $$\sin A=\frac{a}{c}=\frac{1}{\csc A},$$

ⓘ

Symbols:

$\csc z$: cosecant function, $\sin z$: sine function, $A$: angle, $a$: height and $c$: hypotenuse

A&S Ref:

4.3.147

Permalink:

http://dlmf.nist.gov/4.42.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.42(i), §4.42 and Ch.4

►

4.42.2 $$\cos A=\frac{b}{c}=\frac{1}{\sec A},$$

ⓘ

Symbols:

$\cos z$: cosine function, $\sec z$: secant function, $A$: angle, $b$: base and $c$: hypotenuse

A&S Ref:

4.3.147

Permalink:

http://dlmf.nist.gov/4.42.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.42(i), §4.42 and Ch.4

►

4.42.3 $$\tan A=\frac{a}{b}=\frac{1}{\cot A}.$$

ⓘ

Symbols:

$\cot z$: cotangent function, $\tan z$: tangent function, $A$: angle, $a$: height and $b$: base

A&S Ref:

4.3.147

Permalink:

http://dlmf.nist.gov/4.42.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.42(i), §4.42 and Ch.4

… ►

4.42.11 $$\cos a\cos C=\sin a\cot b-\sin C\cot B,$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cot z$: cotangent function, $\sin z$: sine function, $B$: angle, $C$: angle, $a$: arc length and $b$: arc length

Permalink:

http://dlmf.nist.gov/4.42.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §4.42(iii), §4.42 and Ch.4

…

16: 4.20 Derivatives and Differential Equations

§4.20 Derivatives and Differential Equations

… ►

4.20.3 $$\frac{d}{dz}\tan z={\sec }^{2}z,$$

ⓘ

Symbols:

$\frac{df}{dx}$: derivative of $f$ with respect to $x$ , $\sec z$: secant function, $\tan z$: tangent function and $z$: complex variable

A&S Ref:

4.3.107

Permalink:

http://dlmf.nist.gov/4.20.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.20 and Ch.4

… ►

4.20.6 $$\frac{d}{dz}\cot z=-{\csc }^{2}z,$$

ⓘ

Symbols:

$\csc z$: cosecant function, $\cot z$: cotangent function, $\frac{df}{dx}$: derivative of $f$ with respect to $x$ and $z$: complex variable

A&S Ref:

4.3.110

Permalink:

http://dlmf.nist.gov/4.20.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.20 and Ch.4

… ►With $a\ne 0$, the general solutions of the differential equations … ►

4.20.12 $$w=A\cos \left(az\right)+B\sin \left(az\right),$$

ⓘ

Symbols:

$\cos z$: cosine function, $\sin z$: sine function, $a$: real or complex constant, $z$: complex variable, $A$: arbitrary constant and $B$: arbitrary constant

Permalink:

http://dlmf.nist.gov/4.20.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §4.20 and Ch.4

…

17: 4.31 Special Values and Limits

… ►

4.31.1 $$\underset{z\to 0}{lim}\frac{\sinh z}{z}=1,$$

ⓘ

Symbols:

$\sinh z$: hyperbolic sine function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/4.31.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.31 and Ch.4

►

4.31.2 $$\underset{z\to 0}{lim}\frac{\tanh z}{z}=1,$$

ⓘ

Symbols:

$\tanh z$: hyperbolic tangent function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/4.31.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.31 and Ch.4

►

4.31.3 $$\underset{z\to 0}{lim}\frac{\cosh z-1}{z^2}=\frac{1}{2}.$$

ⓘ

Symbols:

$\cosh z$: hyperbolic cosine function and $z$: complex variable

Permalink:

http://dlmf.nist.gov/4.31.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.31 and Ch.4

18: 4.22 Infinite Products and Partial Fractions

§4.22 Infinite Products and Partial Fractions

►

4.22.1 $$\sin z=z\prod _{n=1}^{\mathrm{\infty }}\left(1-\frac{z^2}{n^2{\pi }^2}\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\sin z$: sine function, $n$: integer and $z$: complex variable

A&S Ref:

4.3.89

Permalink:

http://dlmf.nist.gov/4.22.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §4.22 and Ch.4

►

4.22.2 $$\cos z=\prod _{n=1}^{\mathrm{\infty }}\left(1-\frac{4z^2}{{(2n-1)}^2{\pi }^2}\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $n$: integer and $z$: complex variable

A&S Ref:

4.3.90

Permalink:

http://dlmf.nist.gov/4.22.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §4.22 and Ch.4

… ►

4.22.3 $$\cot z=\frac{1}{z}+2z\sum _{n=1}^{\mathrm{\infty }}\frac{1}{z^2-n^2{\pi }^2},$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cot z$: cotangent function, $n$: integer and $z$: complex variable

A&S Ref:

4.3.91

Referenced by:

§22.12

Permalink:

http://dlmf.nist.gov/4.22.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.22 and Ch.4

►

4.22.4 $${\csc }^{2}z=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{{(z-n\pi )}^2},$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\csc z$: cosecant function, $n$: integer and $z$: complex variable

A&S Ref:

4.3.92

Permalink:

http://dlmf.nist.gov/4.22.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §4.22 and Ch.4

…

19: 4.29 Graphics

… ►The surfaces for the complex hyperbolic and inverse hyperbolic functions are similar to the surfaces depicted in §4.15(iii) for the trigonometric and inverse trigonometric functions. …

20: 4.18 Inequalities

§4.18 Inequalities

… ►

4.18.3 $$\cos x\le \frac{\sin x}{x}\le 1,$$ $0\le x\le \pi$,

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\sin z$: sine function and $x$: real variable

A&S Ref:

4.3.81

Referenced by:

§4.18

Permalink:

http://dlmf.nist.gov/4.18.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §4.18, §4.18 and Ch.4

… ►

4.18.5 $$|\sinh y|\le |\sin z|\le \cosh y,$$

ⓘ

Symbols:

$\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $\sin z$: sine function, $y$: real variable and $z$: complex variable

A&S Ref:

4.3.83

Referenced by:

§4.18

Permalink:

http://dlmf.nist.gov/4.18.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §4.18, §4.18 and Ch.4

►

4.18.6 $$|\sinh y|\le |\cos z|\le \cosh y,$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function, $\sinh z$: hyperbolic sine function, $y$: real variable and $z$: complex variable

A&S Ref:

4.3.84

Permalink:

http://dlmf.nist.gov/4.18.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §4.18, §4.18 and Ch.4

… ►

4.18.8 $$|\cos z|\le \cosh |z|,$$

ⓘ

Symbols:

$\cos z$: cosine function, $\cosh z$: hyperbolic cosine function and $z$: complex variable

A&S Ref:

4.3.86

Permalink:

http://dlmf.nist.gov/4.18.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §4.18, §4.18 and Ch.4

…