symmetric elliptic integrals
(0.017 seconds)
11—20 of 51 matching pages
11: 19.34 Mutual Inductance of Coaxial Circles
12: 19.27 Asymptotic Approximations and Expansions
13: 19.1 Special Notation
…
►
►
…
►However, it should be noted that in Chapter 8 of Abramowitz and Stegun (1964) the notation used for elliptic integrals differs from Chapter 17 and is consistent with that used in the present chapter and the rest of the NIST Handbook and DLMF.
…
►
…
| nonnegative integers. | |
| … | |
14: 19.33 Triaxial Ellipsoids
…
►
19.33.1
…
►
§19.33(ii) Potential of a Charged Conducting Ellipsoid
… ►
19.33.5
…
►
19.33.6
…
►
19.33.11
…
15: 19.28 Integrals of Elliptic Integrals
16: 19.20 Special Cases
§19.20 Special Cases
… ►The general lemniscatic case is … ►where may be permuted. … ►The general lemniscatic case is … ►17: 19.32 Conformal Map onto a Rectangle
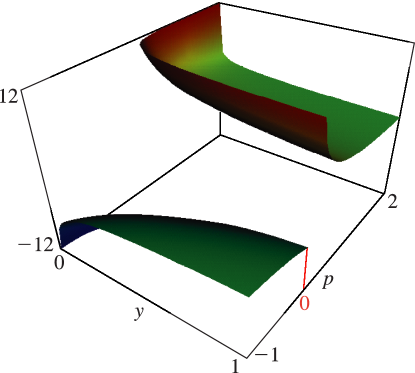
18: 19.17 Graphics
§19.17 Graphics
►See Figures 19.17.1–19.17.8 for symmetric elliptic integrals with real arguments. … ►19: Bille C. Carlson
…
►This symmetry led to the development of symmetric elliptic integrals, which are free from the transformations of modulus and amplitude that complicate the Legendre theory.
…
►This invariance usually replaces sets of twelve equations by sets of three equations and applies also to the relation between the first symmetric elliptic integral and the Jacobian functions.
…