spheroidal differential equation

SearchAdvancedHelp

(0.004 seconds)

1—10 of 31 matching pages

1: 30.2 Differential Equations

… ►

§30.2(i) Spheroidal Differential Equation

… ► … ►The Liouville normal form of equation (30.2.1) is … ►

§30.2(iii) Special Cases

…

2: 30.3 Eigenvalues

§30.3 Eigenvalues

… ►With $\mu =m=0,1,2,\mathrm{\dots }$, the spheroidal wave functions ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$ are solutions of Equation (30.2.1) which are bounded on $(-1,1)$, or equivalently, which are of the form ${(1-x^2)}^{\frac{1}{2}m}g(x)$ where $g(z)$ is an entire function of $z$. … ►

§30.3(iii) Transcendental Equation

… ►

§30.3(iv) Power-Series Expansion

… ►Further coefficients can be found with the Maple program SWF9; see §30.18(i).

3: 30.17 Tables

§30.17 Tables

…

4: 30.9 Asymptotic Approximations and Expansions

§30.9 Asymptotic Approximations and Expansions

… ►

30.9.1 $${\lambda }_n^m\left({\gamma }^2\right)\sim -{\gamma }^2+\gamma q+{\beta }_0+{\beta }_1{\gamma }^{-1}+{\beta }_2{\gamma }^{-2}+\mathrm{\cdots },$$

ⓘ

Symbols:

$\sim$: Poincaré asymptotic expansion, ${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $q$ and ${\beta }_n$: coeffients

A&S Ref:

21.7.6

Referenced by:

item

Permalink:

http://dlmf.nist.gov/30.9.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §30.9(i), §30.9 and Ch.30

… ►

30.9.4 $${\lambda }_n^m\left({\gamma }^2\right)\sim 2q|\gamma |+c_0+c_1{|\gamma |}^{-1}+c_2{|\gamma |}^{-2}+\mathrm{\cdots },$$

ⓘ

Symbols:

$\sim$: Poincaré asymptotic expansion, ${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $q$ and $c_n$: coeffients

A&S Ref:

21.8.2

Referenced by:

item

Permalink:

http://dlmf.nist.gov/30.9.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §30.9(ii), §30.9 and Ch.30

… ►

5: 30.16 Methods of Computation

… ►

§30.16(i) Eigenvalues

… ►

30.16.3 $${\lambda }_n^m\left({\gamma }^2\right)=\underset{d\to \mathrm{\infty }}{lim}{\alpha }_{p,d},$$ $p=\lfloor \frac{1}{2}(n-m)\rfloor +1$.

ⓘ

Symbols:

$\lfloor x\rfloor$: floor of $x$ , ${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, $d$: dimension, ${\alpha }_{j,k}$: real eigenvalues and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.16.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §30.16(i), §30.16 and Ch.30

… ►

30.16.4 $${\alpha }_{p,d}-{\lambda }_n^m\left({\gamma }^2\right)=O\left(\frac{{\gamma }^{4d}}{4^{2d+1}{((m+2d-1)!(m+2d+1)!)}^2}\right),$$ $d\to \mathrm{\infty }$.

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, $!$: factorial (as in $n!$), ${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, $d$: dimension, ${\alpha }_{j,k}$: real eigenvalues and ${\gamma }^2$: real parameter

Permalink:

http://dlmf.nist.gov/30.16.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §30.16(i), §30.16 and Ch.30

… ►If ${\lambda }_n^m\left({\gamma }^2\right)$ is known, then we can compute ${\mathrm{𝖯𝗌}}_n^m(x,{\gamma }^2)$ (not normalized) by solving the differential equation (30.2.1) numerically with initial conditions $w(0)=1$, $w^{\prime }(0)=0$ if $n-m$ is even, or $w(0)=0$, $w^{\prime }(0)=1$ if $n-m$ is odd. …

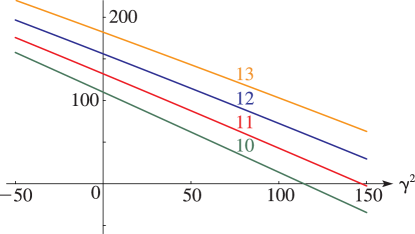
6: 30.7 Graphics

… ►

§30.7(i) Eigenvalues

… ►

►►

Figure 30.7.4: Eigenvalues ${\lambda }_n^{10}\left({\gamma }^2\right)$, $n=10,11,12,13$, $-50\le {\gamma }^2\le 150$. Magnify

…

7: 30.6 Functions of Complex Argument

… ►

8: 30.8 Expansions in Series of Ferrers Functions

… ►

30.8.4 $$A_k{f}_{k-1}+\left(B_k-{\lambda }_n^m\left({\gamma }^2\right)\right)f_k+C_k{f}_{k+1}=0,$$

ⓘ

Symbols:

${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $A_k$ , $B_k$ and $C_k$

Referenced by:

§30.16(ii), §30.8(ii)

Permalink:

http://dlmf.nist.gov/30.8.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §30.8(i), §30.8 and Ch.30

… ►

30.8.8 $$\frac{{\lambda }_n^m\left({\gamma }^2\right)-B_k}{A_k}\frac{a_{n,k}^m({\gamma }^2)}{a_{n,k-1}^m({\gamma }^2)}=1+O\left(\frac{1}{k^4}\right).$$

ⓘ

Symbols:

$O\left(x\right)$: order not exceeding, ${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $a_{n,k}^m({\gamma }^2)$: coefficients, $A_k$ and $B_k$

Permalink:

http://dlmf.nist.gov/30.8.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §30.8(i), §30.8 and Ch.30

… ►

30.8.10 $$A_{-N-1}a_{}^{\prime }{}_{n,-N-2}{}^m({\gamma }^2)+\left(B_{-N-1}-{\lambda }_n^m\left({\gamma }^2\right)\right)a_{}^{\prime }{}_{n,-N-1}{}^m({\gamma }^2)+C^{\prime }{a}_{n,-N}^m({\gamma }^2)=0,$$

ⓘ

Symbols:

${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, $a_{n,k}^m({\gamma }^2)$: coefficients, $A_k$ , $B_k$ , $N$: upper limit and $C^{\prime }$

Permalink:

http://dlmf.nist.gov/30.8.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §30.8(ii), §30.8 and Ch.30

…

9: 30.1 Special Notation

… ►Flammer (1957) and Abramowitz and Stegun (1964) use ${\lambda }_{mn}(\gamma )$ for ${\lambda }_n^m\left({\gamma }^2\right)+{\gamma }^2$, $R_{mn}^{(j)}(\gamma ,z)$ for $S_n^{m(j)}(z,\gamma )$, and …

10: 30.4 Functions of the First Kind

… ►

30.4.5 $${\alpha }_k{g}_{k+2}+({\beta }_k-{\lambda }_n^m\left({\gamma }^2\right))g_k+{\gamma }_k{g}_{k-2}=0$$

ⓘ

Symbols:

${\lambda }_n^m\left({\gamma }^2\right)$: eigenvalues of the spheroidal differential equation, $m$: nonnegative integer, $n\ge m$: integer degree, ${\gamma }^2$: real parameter, ${\alpha }_k$: coefficent, ${\beta }_k$: coefficent and ${\gamma }_k$: coefficent

A&S Ref:

21.7.18

Permalink:

http://dlmf.nist.gov/30.4.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §30.4(iii), §30.4 and Ch.30

…