spherical trigonometry

SearchAdvancedHelp

(0.001 seconds)

1—10 of 85 matching pages

1: 14.30 Spherical and Spheroidal Harmonics

… ►

§14.30(i) Definitions

… ► … ►

§14.30(iii) Sums

►

Distributional Completeness

… ►

2: 22.18 Mathematical Applications

… ►Discussion of parametrization of the angles of spherical trigonometry in terms of Jacobian elliptic functions is given in Greenhill (1959, p. 131) and Lawden (1989, §4.4). …

3: 10.55 Continued Fractions

§10.55 Continued Fractions

►For continued fractions for ${𝗃}_{n+1}\left(z\right)/{𝗃}_n\left(z\right)$ and ${𝗂}_{n+1}^{(1)}\left(z\right)/{𝗂}_n^{(1)}\left(z\right)$ see Cuyt et al. (2008, pp. 350, 353, 362, 363, 367–369).

4: 10.48 Graphs

§10.48 Graphs

… ►

►►

Figure 10.48.5: ${𝗂}_0^{(1)}\left(x\right)$, ${𝗂}_0^{(2)}\left(x\right)$, ${𝗄}_0\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.6: ${𝗂}_1^{(1)}\left(x\right),{𝗂}_1^{(2)}\left(x\right),{𝗄}_1\left(x\right)$, $0\le x\le 4$. Magnify

►

►►

Figure 10.48.7: ${𝗂}_5^{(1)}\left(x\right)$, ${𝗂}_5^{(2)}\left(x\right)$, ${𝗄}_5\left(x\right)$, $0\le x\le 8$. Magnify

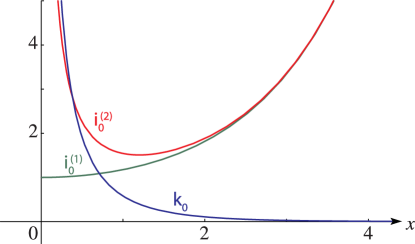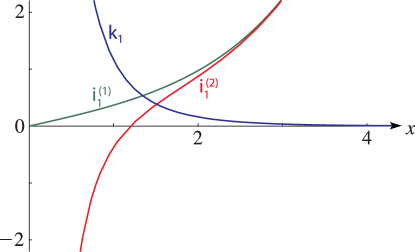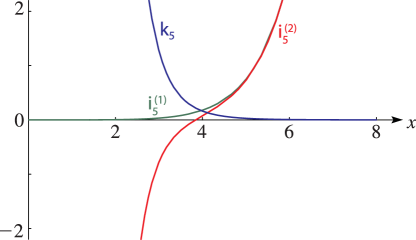5: 10.52 Limiting Forms

§10.52 Limiting Forms

… ►

10.52.1 $${𝗃}_n\left(z\right),{𝗂}_n^{(1)}\left(z\right)\sim z^n/(2n+1)!!,$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $!!$: double factorial, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.4

Permalink:

http://dlmf.nist.gov/10.52.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

►

10.52.2 $$-{𝗒}_n\left(z\right),\mathrm{i}{𝗁}_n^{(1)}\left(z\right),-\mathrm{i}{𝗁}_n^{(2)}\left(z\right),{(-1)}^n{𝗂}_n^{(2)}\left(z\right),(2/\pi ){𝗄}_n\left(z\right)\sim (2n-1)!!/z^{n+1}.$$

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $!!$: double factorial, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, ${𝗄}_n\left(z\right)$: modified spherical Bessel function, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, ${𝗁}_n^{(1)}\left(z\right)$: spherical Bessel function of the third kind, ${𝗁}_n^{(2)}\left(z\right)$: spherical Bessel function of the third kind, $n$: integer and $z$: complex variable

A&S Ref:

10.1.5

Permalink:

http://dlmf.nist.gov/10.52.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(i), §10.52 and Ch.10

… ►

${𝗁}_n^{(1)}\left(z\right)\sim {\mathrm{i}}^{-n-1}{z}^{-1}{\mathrm{e}}^{\mathrm{i}z},$

… ►

10.52.5 $${𝗂}_n^{(1)}\left(z\right)\sim {𝗂}_n^{(2)}\left(z\right)\sim \frac{1}{2}{z}^{-1}{\mathrm{e}}^z,$$ ,

ⓘ

Symbols:

$\sim$: asymptotic equality, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{ph}$: phase, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $z$: complex variable and $\delta$: small positive constant

Permalink:

http://dlmf.nist.gov/10.52.E5

Encodings:

pMML, png, TeX

See also:

Annotations for §10.52(ii), §10.52 and Ch.10

…

6: 10.50 Wronskians and Cross-Products

§10.50 Wronskians and Cross-Products

… ►

$$𝒲\left\{{𝗁}_n^{(1)}\left(z\right),{𝗁}_n^{(2)}\left(z\right)\right\}=-2\mathrm{i}{z}^{-2}.$$

►

$$𝒲\left\{{𝗂}_n^{(1)}\left(z\right),{𝗂}_n^{(2)}\left(z\right)\right\}={(-1)}^{n+1}{z}^{-2},$$

►

$$𝒲\left\{{𝗂}_n^{(1)}\left(z\right),{𝗄}_n\left(z\right)\right\}=𝒲\left\{{𝗂}_n^{(2)}\left(z\right),{𝗄}_n\left(z\right)\right\}=-\frac{1}{2}\pi z^{-2}.$$

… ►Results corresponding to (10.50.3) and (10.50.4) for ${𝗂}_n^{(1)}\left(z\right)$ and ${𝗂}_n^{(2)}\left(z\right)$ are obtainable via (10.47.12).

7: 10.47 Definitions and Basic Properties

… ► … ►

Equation (10.47.1)

… ►

Equation (10.47.2)

… ► … ►

§10.47(iv) Interrelations

…

8: 10.49 Explicit Formulas

… ►

§10.49(i) Unmodified Functions

… ►

§10.49(ii) Modified Functions

… ►

§10.49(iii) Rayleigh’s Formulas

… ►

§10.49(iv) Sums or Differences of Squares

… ►

${\left({𝗂}_0^{(1)}\left(z\right)\right)}^2-{\left({𝗂}_0^{(2)}\left(z\right)\right)}^2=-z^{-2},$

…

9: 10.53 Power Series

§10.53 Power Series

… ►

10.53.3 $${𝗂}_n^{(1)}\left(z\right)=z^n\sum _{k=0}^{\mathrm{\infty }}\frac{{(\frac{1}{2}{z}^2)}^k}{k!(2n+2k+1)!!},$$

ⓘ

Symbols:

$!!$: double factorial, $!$: factorial (as in $n!$), ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

10.2.5

Referenced by:

§10.53

Permalink:

http://dlmf.nist.gov/10.53.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.53 and Ch.10

►

10.53.4 $${𝗂}_n^{(2)}\left(z\right)=\frac{{(-1)}^n}{z^{n+1}}\sum _{k=0}^n\frac{(2n-2k-1)!!{(-\frac{1}{2}{z}^2)}^k}{k!}+\frac{1}{z^{n+1}}\sum _{k=n+1}^{\mathrm{\infty }}\frac{{(\frac{1}{2}{z}^2)}^k}{k!(2k-2n-1)!!}.$$

ⓘ

Symbols:

$!!$: double factorial, $!$: factorial (as in $n!$), ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer, $k$: nonnegative integer and $z$: complex variable

A&S Ref:

10.2.6

Referenced by:

§10.53

Permalink:

http://dlmf.nist.gov/10.53.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.53 and Ch.10

►For ${𝗁}_n^{(1)}\left(z\right)$ and ${𝗁}_n^{(2)}\left(z\right)$ combine (10.47.10), (10.53.1), and (10.53.2). For ${𝗄}_n\left(z\right)$ combine (10.47.11), (10.53.3), and (10.53.4).

10: 10.56 Generating Functions

§10.56 Generating Functions

… ►

10.56.1 $$\frac{\cos \sqrt{z^2-2zt}}{z}=\frac{\cos z}{z}+\sum _{n=1}^{\mathrm{\infty }}\frac{t^n}{n!}{𝗃}_{n-1}\left(z\right),$$

ⓘ

Symbols:

$\cos z$: cosine function, $!$: factorial (as in $n!$), ${𝗃}_n\left(z\right)$: spherical Bessel function of the first kind, $n$: integer and $z$: complex variable

Referenced by:

§10.56, Ch.10

Permalink:

http://dlmf.nist.gov/10.56.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

►

10.56.2 $$\frac{\sin \sqrt{z^2-2zt}}{z}=\frac{\sin z}{z}+\sum _{n=1}^{\mathrm{\infty }}\frac{t^n}{n!}{𝗒}_{n-1}\left(z\right).$$

ⓘ

Symbols:

$!$: factorial (as in $n!$), $\sin z$: sine function, ${𝗒}_n\left(z\right)$: spherical Bessel function of the second kind, $n$: integer and $z$: complex variable

Referenced by:

§10.56

Permalink:

http://dlmf.nist.gov/10.56.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

►

10.56.3 $$\frac{\cosh \sqrt{z^2+2\mathrm{i}zt}}{z}=\frac{\cosh z}{z}+\sum _{n=1}^{\mathrm{\infty }}\frac{{(\mathrm{i}t)}^n}{n!}{𝗂}_{n-1}^{(1)}\left(z\right),$$

ⓘ

Symbols:

$!$: factorial (as in $n!$), $\cosh z$: hyperbolic cosine function, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(1)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.56

Permalink:

http://dlmf.nist.gov/10.56.E3

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

►

10.56.4 $$\frac{\sinh \sqrt{z^2+2\mathrm{i}zt}}{z}=\frac{\sinh z}{z}+\sum _{n=1}^{\mathrm{\infty }}\frac{{(\mathrm{i}t)}^n}{n!}{𝗂}_{n-1}^{(2)}\left(z\right),$$

ⓘ

Symbols:

$!$: factorial (as in $n!$), $\sinh z$: hyperbolic sine function, $\mathrm{i}$: imaginary unit, ${𝗂}_n^{(2)}\left(z\right)$: modified spherical Bessel function, $n$: integer and $z$: complex variable

Referenced by:

§10.56

Permalink:

http://dlmf.nist.gov/10.56.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §10.56 and Ch.10

…