sine integrals

SearchAdvancedHelp

(0.010 seconds)

11—20 of 174 matching pages

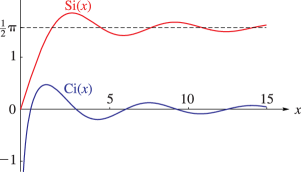
11: 6.3 Graphics

… ►

►►

Figure 6.3.2: The sine and cosine integrals $\mathrm{Si}\left(x\right),\mathrm{Ci}\left(x\right)$, $0\le x\le 15$. Magnify

…

12: 7.4 Symmetry

… ►

$S\left(-z\right)=-S\left(z\right),$

… ►

$S\left(\mathrm{i}z\right)=-\mathrm{i}S\left(z\right).$

… ►

$\mathrm{g}\left(-z\right)=\sqrt{2}\sin \left(\frac{1}{4}\pi +\frac{1}{2}\pi z^2\right)-\mathrm{g}\left(z\right).$

13: 6.4 Analytic Continuation

… ►

6.4.6 $$\mathrm{f}\left(z{\mathrm{e}}^{\pm \pi \mathrm{i}}\right)=\pi {\mathrm{e}}^{\mp \mathrm{i}z}-\mathrm{f}\left(z\right),$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{f}\left(z\right)$: auxiliary function for sine and cosine integrals and $z$: complex variable

Referenced by:

§6.12(ii), §6.4

Permalink:

http://dlmf.nist.gov/6.4.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §6.4 and Ch.6

►

6.4.7 $$\mathrm{g}\left(z{\mathrm{e}}^{\pm \pi \mathrm{i}}\right)=\mp \pi \mathrm{i}{\mathrm{e}}^{\mp \mathrm{i}z}+\mathrm{g}\left(z\right).$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\mathrm{g}\left(z\right)$: auxiliary function for sine and cosine integrals and $z$: complex variable

Referenced by:

§6.12(ii), §6.4

Permalink:

http://dlmf.nist.gov/6.4.E7

Encodings:

pMML, png, TeX

See also:

Annotations for §6.4 and Ch.6

►Unless indicated otherwise, in the rest of this chapter and elsewhere in the DLMF the functions $E_1\left(z\right)$, $\mathrm{Ci}\left(z\right)$, $\mathrm{Chi}\left(z\right)$, $\mathrm{f}\left(z\right)$, and $\mathrm{g}\left(z\right)$ assume their principal values, that is, the branches that are real on the positive real axis and two-valued on the negative real axis.

14: 6.13 Zeros

… ►

6.13.1 $$x_0=\mathrm{0.37250\hspace{0.33em}74107\hspace{0.33em}81366\hspace{0.33em}63446\hspace{0.33em}19918\hspace{0.33em}66580}\mathrm{\dots }.$$

ⓘ

Symbols:

$x$: real variable

Notes:

For more digits see OEIS Sequence A091723; see also Sloane (2003).

Referenced by:

§6.13

Permalink:

http://dlmf.nist.gov/6.13.E1

Encodings:

pMML, png, TeX

See also:

Annotations for §6.13 and Ch.6

► $\mathrm{Ci}\left(x\right)$ and $\mathrm{si}\left(x\right)$ each have an infinite number of positive real zeros, which are denoted by $c_k$, $s_k$, respectively, arranged in ascending order of absolute value for $k=0,1,2,\mathrm{\dots }$. Values of $c_1$ and $c_2$ to 30D are given by MacLeod (1996b). … ►

6.13.2 $$c_k,s_k\sim \alpha +\frac{1}{\alpha }-\frac{16}{3}\frac{1}{{\alpha }^3}+\frac{1673}{15}\frac{1}{{\alpha }^5}-\frac{\mathrm{5\hspace{0.33em}07746}}{105}\frac{1}{{\alpha }^7}+\mathrm{\cdots },$$

ⓘ

Symbols:

$\sim$: Poincaré asymptotic expansion, $c_k$: zeros of $\mathrm{Ci}\left(x\right)$ and $s_k$: zeros of $\mathrm{Si}\left(x\right)$

Referenced by:

§6.13, §6.18(iii)

Permalink:

http://dlmf.nist.gov/6.13.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §6.13 and Ch.6

…

15: 6.18 Methods of Computation

§6.18 Methods of Computation

… ►Power series, asymptotic expansions, and quadrature can also be used to compute the functions $\mathrm{f}\left(z\right)$ and $\mathrm{g}\left(z\right)$. …Then $\mathrm{f}\left(z\right)=B_0$, $\mathrm{g}\left(z\right)=A_0$, and … ►

§6.18(iii) Zeros

►Zeros of $\mathrm{Ci}\left(x\right)$ and $\mathrm{si}\left(x\right)$ can be computed to high precision by Newton’s rule (§3.8(ii)), using values supplied by the asymptotic expansion (6.13.2) as initial approximations. …

16: 7.5 Interrelations

… ►

7.5.2 $$C\left(z\right)+\mathrm{i}S\left(z\right)=\frac{1}{2}(1+\mathrm{i})-ℱ\left(z\right).$$

ⓘ

Symbols:

$C\left(z\right)$: Fresnel integral, $ℱ\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $\mathrm{i}$: imaginary unit and $z$: complex variable

Referenced by:

§7.5

Permalink:

http://dlmf.nist.gov/7.5.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

… ►

7.5.4 $$S\left(z\right)=\frac{1}{2}-\mathrm{f}\left(z\right)\cos \left(\frac{1}{2}\pi z^2\right)-\mathrm{g}\left(z\right)\sin \left(\frac{1}{2}\pi z^2\right).$$

ⓘ

Symbols:

$\mathrm{f}\left(z\right)$: auxiliary function for Fresnel integrals, $\mathrm{g}\left(z\right)$: auxiliary function for Fresnel integrals, $S\left(z\right)$: Fresnel integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\sin z$: sine function and $z$: complex variable

A&S Ref:

7.3.10

Referenced by:

§7.12(ii), §7.5

Permalink:

http://dlmf.nist.gov/7.5.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

… ►

7.5.6 $${\mathrm{e}}^{\pm \frac{1}{2}\pi \mathrm{i}{z}^2}(\mathrm{g}\left(z\right)\pm \mathrm{i}\mathrm{f}\left(z\right))=\frac{1}{2}(1\pm \mathrm{i})-(C\left(z\right)\pm \mathrm{i}S\left(z\right)).$$

ⓘ

Symbols:

$\mathrm{f}\left(z\right)$: auxiliary function for Fresnel integrals, $\mathrm{g}\left(z\right)$: auxiliary function for Fresnel integrals, $C\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit and $z$: complex variable

Referenced by:

§7.5

Permalink:

http://dlmf.nist.gov/7.5.E6

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

… ►

7.5.8 $$C\left(z\right)\pm \mathrm{i}S\left(z\right)=\frac{1}{2}(1\pm \mathrm{i})\mathrm{erf}\zeta .$$

ⓘ

Symbols:

$C\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $\mathrm{erf}z$: error function, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\zeta$: change of variable

Referenced by:

§7.5, §7.5, §7.6(i)

Permalink:

http://dlmf.nist.gov/7.5.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

►

7.5.9 $$C\left(z\right)\pm \mathrm{i}S\left(z\right)=\frac{1}{2}(1\pm \mathrm{i})\left(1-{\mathrm{e}}^{\pm \frac{1}{2}\pi \mathrm{i}{z}^2}w\left(\mathrm{i}\zeta \right)\right).$$

ⓘ

Symbols:

$C\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $\pi$: the ratio of the circumference of a circle to its diameter, $w\left(z\right)$: Faddeeva (or Faddeyeva) function, $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $z$: complex variable and $\zeta$: change of variable

Referenced by:

§7.5

Permalink:

http://dlmf.nist.gov/7.5.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §7.5 and Ch.7

…

17: 8.1 Special Notation

… ►Unless otherwise indicated, primes denote derivatives with respect to the argument. ►The functions treated in this chapter are the incomplete gamma functions $\gamma (a,z)$, $\mathrm{\Gamma }(a,z)$, ${\gamma }^{\ast }(a,z)$, $P(a,z)$, and $Q(a,z)$; the incomplete beta functions ${\mathrm{B}}_x(a,b)$ and $I_x(a,b)$; the generalized exponential integral $E_p\left(z\right)$; the generalized sine and cosine integrals $\mathrm{si}(a,z)$, $\mathrm{ci}(a,z)$, $\mathrm{Si}(a,z)$, and $\mathrm{Ci}(a,z)$. ►Alternative notations include: Prym’s functions $P_z(a)=\gamma (a,z)$, $Q_z(a)=\mathrm{\Gamma }(a,z)$, Nielsen (1906a, pp. 25–26), Batchelder (1967, p. 63); $(a,z)!=\gamma (a+1,z)$, $[a,z]!=\mathrm{\Gamma }(a+1,z)$, Dingle (1973); $B(a,b,x)={\mathrm{B}}_x(a,b)$, $I(a,b,x)=I_x(a,b)$, Magnus et al. (1966); $\mathrm{Si}(a,x)\to \mathrm{Si}(1-a,x)$, $\mathrm{Ci}(a,x)\to \mathrm{Ci}(1-a,x)$, Luke (1975).

18: 7.2 Definitions

… ►

7.2.8 $$S\left(z\right)={\int }_0^z\sin \left(\frac{1}{2}\pi t^2\right)dt,$$

ⓘ

Defines:

$S\left(z\right)$: Fresnel integral

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\int$: integral, $\sin z$: sine function and $z$: complex variable

A&S Ref:

7.3.2

Referenced by:

§7.5, §7.6(i)

Permalink:

http://dlmf.nist.gov/7.2.E8

Encodings:

pMML, png, TeX

See also:

Annotations for §7.2(iii), §7.2 and Ch.7

► $ℱ\left(z\right)$, $C\left(z\right)$, and $S\left(z\right)$ are entire functions of $z$, as are $\mathrm{f}\left(z\right)$ and $\mathrm{g}\left(z\right)$ in the next subsection. … ►

$\underset{x\to \mathrm{\infty }}{lim}S\left(x\right)=\frac{1}{2}.$

… ►

7.2.10 $$\mathrm{f}\left(z\right)=\left(\frac{1}{2}-S\left(z\right)\right)\cos \left(\frac{1}{2}\pi z^2\right)-\left(\frac{1}{2}-C\left(z\right)\right)\sin \left(\frac{1}{2}\pi z^2\right),$$

ⓘ

Defines:

$\mathrm{f}\left(z\right)$: auxiliary function for Fresnel integrals

Symbols:

$C\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\sin z$: sine function and $z$: complex variable

A&S Ref:

7.3.5

Referenced by:

§7.4, §7.5

Permalink:

http://dlmf.nist.gov/7.2.E10

Encodings:

pMML, png, TeX

See also:

Annotations for §7.2(iv), §7.2 and Ch.7

►

7.2.11 $$\mathrm{g}\left(z\right)=\left(\frac{1}{2}-C\left(z\right)\right)\cos \left(\frac{1}{2}\pi z^2\right)+\left(\frac{1}{2}-S\left(z\right)\right)\sin \left(\frac{1}{2}\pi z^2\right).$$

ⓘ

Defines:

$\mathrm{g}\left(z\right)$: auxiliary function for Fresnel integrals

Symbols:

$C\left(z\right)$: Fresnel integral, $S\left(z\right)$: Fresnel integral, $\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $\sin z$: sine function and $z$: complex variable

A&S Ref:

7.3.6

Referenced by:

§7.4, §7.5

Permalink:

http://dlmf.nist.gov/7.2.E11

Encodings:

pMML, png, TeX

See also:

Annotations for §7.2(iv), §7.2 and Ch.7

…

19: 7.25 Software

… ►

§7.25(iv) $C\left(x\right)$, $S\left(x\right)$, $\mathrm{f}\left(x\right)$, $\mathrm{g}\left(x\right)$, $x\in ℝ$

… ►

§7.25(v) $C\left(z\right)$, $S\left(z\right)$, $z\in ℂ$

…

20: 6.7 Integral Representations

… ►

§6.7(ii) Sine and Cosine Integrals

… ►

6.7.9 $$\mathrm{si}\left(z\right)=-{\int }_0^{\pi /2}{\mathrm{e}}^{-z\cos t}\cos \left(z\sin t\right)dt,$$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $\cos z$: cosine function, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\mathrm{si}\left(z\right)$: sine integral, $\sin z$: sine function and $z$: complex variable

A&S Ref:

5.2.10

Permalink:

http://dlmf.nist.gov/6.7.E9

Encodings:

pMML, png, TeX

See also:

Annotations for §6.7(ii), §6.7 and Ch.6

… ►

6.7.12 $$\mathrm{g}\left(z\right)+\mathrm{i}\mathrm{f}\left(z\right)={\mathrm{e}}^{-\mathrm{i}z}{\int }_z^{\mathrm{\infty }}\frac{{\mathrm{e}}^{\mathrm{i}t}}{t}dt,$$ $|\mathrm{ph}z|\le \pi .$

ⓘ

Symbols:

$\pi$: the ratio of the circumference of a circle to its diameter, $dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\mathrm{i}$: imaginary unit, $\int$: integral, $\mathrm{ph}$: phase, $\mathrm{f}\left(z\right)$: auxiliary function for sine and cosine integrals, $\mathrm{g}\left(z\right)$: auxiliary function for sine and cosine integrals and $z$: complex variable

Referenced by:

§6.7(iii)

Permalink:

http://dlmf.nist.gov/6.7.E12

Encodings:

pMML, png, TeX

See also:

Annotations for §6.7(iii), §6.7 and Ch.6

… ►

6.7.13 $$\mathrm{f}\left(z\right)={\int }_0^{\mathrm{\infty }}\frac{\sin t}{t+z}dt={\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{-zt}}{t^2+1}dt,$$

ⓘ

Symbols:

$dx$: differential of $x$ , $\mathrm{e}$: base of natural logarithm, $\int$: integral, $\sin z$: sine function, $\mathrm{f}\left(z\right)$: auxiliary function for sine and cosine integrals and $z$: complex variable

Referenced by:

§6.12(ii), §6.7(iii)

Permalink:

http://dlmf.nist.gov/6.7.E13

Encodings:

pMML, png, TeX

See also:

Annotations for §6.7(iii), §6.7 and Ch.6

… ►

6.7.16 $$\mathrm{g}\left(z\right)=2{\int }_0^{\mathrm{\infty }}{K}_0\left(2\sqrt{zt}\right)\sin tdt.$$

ⓘ

Symbols:

$dx$: differential of $x$ , $\int$: integral, $K_{\nu }\left(z\right)$: modified Bessel function of the second kind, $\sin z$: sine function, $\mathrm{g}\left(z\right)$: auxiliary function for sine and cosine integrals and $z$: complex variable

Referenced by:

§6.7(iii)

Permalink:

http://dlmf.nist.gov/6.7.E16

Encodings:

pMML, png, TeX

See also:

Annotations for §6.7(iii), §6.7 and Ch.6

…