scaled Riemann theta functions

SearchAdvancedHelp

(0.004 seconds)

4 matching pages

1: 21.4 Graphics

… ►Figure 21.4.1 provides surfaces of the scaled Riemann theta function $\widehat{\theta }\left(𝐳\right|𝛀)$, with … ►For the scaled Riemann theta functions depicted in Figures 21.4.2–21.4.5 … ►

►

►

Figure 21.4.4: A real-valued scaled Riemann theta function: $\widehat{\theta }\left(\mathrm{i}x,\mathrm{i}y\right|{𝛀}_1)$, $0\le x\le 4$, $0\le y\le 4$. … Magnify 3D Help

►

►

►

Figure 21.4.5: The real part of a genus 3 scaled Riemann theta function: $\mathrm{\Re }\widehat{\theta }\left(x+\mathrm{i}y,0,0\right|{𝛀}_2)$, $0\le x\le 1$, $0\le y\le 3$. … Magnify 3D Help

2: 21.2 Definitions

… ► $\theta \left(𝐳\right|𝛀)$ is also referred to as a theta function with $g$ components, a $g$-dimensional theta function or as a genus $g$ theta function. ►For numerical purposes we use the scaled Riemann theta function $\widehat{\theta }\left(𝐳\right|𝛀)$, defined by (Deconinck et al. (2004)), ►

21.2.2 $$\widehat{\theta }\left(𝐳\right|𝛀)={\mathrm{e}}^{-\pi [\mathrm{\Im }𝐳]\cdot {[\mathrm{\Im }𝛀]}^{-1}\cdot [\mathrm{\Im }𝐳]}\theta \left(𝐳\right|𝛀).$$

ⓘ

Defines:

$\widehat{\theta }\left(𝐳\right|𝛀)$: scaled Riemann theta function

Symbols:

$\theta \left(𝐳\right|𝛀)$: Riemann theta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm, $\mathrm{\Im }$: imaginary part and $𝛀$: a Riemann matrix

Permalink:

http://dlmf.nist.gov/21.2.E2

Encodings:

pMML, png, TeX

See also:

Annotations for §21.2(i), §21.2 and Ch.21

… ►

21.2.4

ⓘ

Symbols:

$\widehat{\theta }\left(𝐳\right|𝛀)$: scaled Riemann theta function, $\pi$: the ratio of the circumference of a circle to its diameter, $\mathrm{e}$: base of natural logarithm and $\mathrm{i}$: imaginary unit

Permalink:

http://dlmf.nist.gov/21.2.E4

Encodings:

pMML, png, TeX

See also:

Annotations for §21.2(i), §21.2(i), §21.2 and Ch.21

…

3: 21.9 Integrable Equations

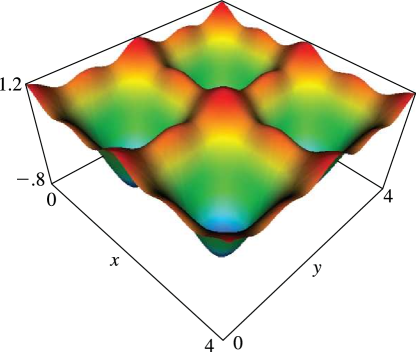
§21.9 Integrable Equations

… ►Typical examples of such equations are the Korteweg–de Vries equation …Here, and in what follows, $x,y$, and $t$ suffixes indicate partial derivatives. … ► … ►

4: Errata

… ►

In previous versions of the DLMF, in §8.18(ii), the notation $\tilde{\mathrm{\Gamma }}(z)$ was used for the scaled gamma function ${\mathrm{\Gamma }}^{\ast }\left(z\right)$. Now in §8.18(ii), we adopt the notation which was introduced in Version 1.1.7 (October 15, 2022) and correspondingly, Equation (8.18.13) has been removed. In place of Equation (8.18.13), it is now mentioned to see (5.11.3).

… ►

Equations: (5.9.2_5), (5.9.10_1), (5.9.10_2), (5.9.11_1), (5.9.11_2), the definition of the scaled gamma function ${\mathrm{\Gamma }}^{\ast }\left(z\right)$ was inserted after the first equals sign in (5.11.3), post equality added in (7.17.2) which gives “$={\sum }_{m=0}^{\mathrm{\infty }}{a}_m{t}^{2m+1}$”, (7.17.2_5), (31.11.3_1), (31.11.3_2) with some explanatory text.

… ►

The Weierstrass zeta function was incorrectly linked to the definition of the Riemann zeta function. However, to the eye, the function appeared correct. The link was corrected.

… ►

The original constraint, $\mathrm{\Re }s>0$, was removed because, as stated after (25.2.1), $\zeta \left(s\right)$ is meromorphic with a simple pole at $s=1$, and therefore $\zeta \left(s\right)-{(s-1)}^{-1}$ is an entire function.

Suggested by John Harper.

… ►

21.3.4 $$\theta \left[\genfrac{}{}{0.0pt}{}{𝜶+{𝐦}_1}{𝜷+{𝐦}_2}\right]\left(𝐳\right|𝛀)={\mathrm{e}}^{2\pi \mathrm{i}𝜶\cdot {𝐦}_2}\theta \left[\genfrac{}{}{0.0pt}{}{𝜶}{𝜷}\right]\left(𝐳\right|𝛀)$$

Originally the vector ${𝐦}_2$ on the right-hand side was given incorrectly as ${𝐦}_1$.

Reported 2012-08-27 by Klaas Vantournhout.

…