region

(0.001 seconds)

1—10 of 60 matching pages

1: 28.17 Stability as $x\to\pm\infty$

§28.17 Stability as $x\to\pm\infty$

… ►For real

a

and

q

(\neq 0)

the stable regions are the open regions indicated in color in Figure 28.17.1. The boundary of each region comprises the characteristic curves

a=a_{n}\left(q\right)

and

a=b_{n}\left(q\right)

; compare Figure 28.2.1. … ►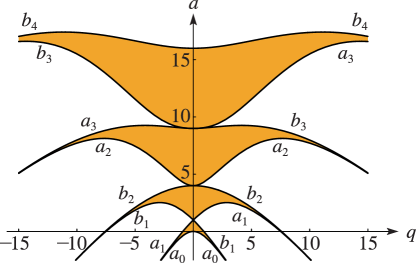

See accompanying text — Figure 28.17.1: Stability chart for eigenvalues of Mathieu’s equation (28.2.1). Magnify

2: 12.20 Approximations

… ►Luke (1969b, pp. 25 and 35) gives Chebyshev-series expansions for the confluent hypergeometric functions

U\left(a,b,x\right)

and

M\left(a,b,x\right)

(§13.2(i)) whose regions of validity include intervals with endpoints

x=\infty

and

x=0

, respectively. …

3: 10.72 Mathematical Applications

… ►In regions in which (10.72.1) has a simple turning point

z_{0}

, that is,

f(z)

and

g(z)

are analytic (or with weaker conditions if

z=x

is a real variable) and

z_{0}

is a simple zero of

f(z)

, asymptotic expansions of the solutions

w

for large

u

can be constructed in terms of Airy functions or equivalently Bessel functions or modified Bessel functions of order

\tfrac{1}{3}

(§9.6(i)). These expansions are uniform with respect to

z

, including the turning point

z_{0}

and its neighborhood, and the region of validity often includes cut neighborhoods (§1.10(vi)) of other singularities of the differential equation, especially irregular singularities. … ►In regions in which the function

f(z)

has a simple pole at

z=z_{0}

and

(z-z_{0})^{2}g(z)

is analytic at

z=z_{0}

(the case

\lambda=-1

in §10.72(i)), asymptotic expansions of the solutions

w

of (10.72.1) for large

u

can be constructed in terms of Bessel functions and modified Bessel functions of order

\pm\sqrt{1+4\rho}

, where

\rho

is the limiting value of

(z-z_{0})^{2}g(z)

z\to z_{0}

. These asymptotic expansions are uniform with respect to

z

, including cut neighborhoods of

z_{0}

, and again the region of uniformity often includes cut neighborhoods of other singularities of the differential equation. …

4: 21.10 Methods of Computation

… ►

•

Belokolos et al. (1994, Chapter 5) and references therein. Here the Riemann surface is represented by the action of a Schottky group on a region of the complex plane. The same representation is used in Gianni et al. (1998).

…

5: Bonita V. Saunders

… ►This work has resulted in several published papers presented as contributed or invited talks at universities and regional, national, and international conferences. …

6: 5.10 Continued Fractions

… ►

5.10.1

\operatorname{Ln}\Gamma\left(z\right)+z-\left(z-\tfrac{1}{2}\right)\ln z-% \tfrac{1}{2}\ln\left(2\pi\right)=\cfrac{a_{0}}{z+\cfrac{a_{1}}{z+\cfrac{a_{2}}% {z+\cfrac{a_{3}}{z+\cfrac{a_{4}}{z+\cfrac{a_{5}}{z+}}}}}}\cdots,

ⓘ

Symbols:: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\pi$ : the ratio of the circumference of a circle to its diameter, $\operatorname{Ln}\NVar{z}$ : general logarithm function, $\ln\NVar{z}$ : principal branch of logarithm function, $z$ : complex variable and $a_{k}$ : coefficient
Referenced by:: Erratum (V1.0.10) for Equations (5.9.10), (5.9.11), (5.10.1), (5.11.1), (5.11.8)
Permalink:: http://dlmf.nist.gov/5.10.E1
Encodings:: pMML, png, TeX
Addition (effective with 1.0.10):: To increase the region of validity of this equation, the logarithm of the gamma function that appears on its left-hand side has been changed to $\operatorname{Ln}\Gamma\left(z\right)$ , where $\operatorname{Ln}$ is the general logarithm. Originally $\ln\Gamma\left(z\right)$ was used, where $\ln$ is the principal branch of the logarithm.
Suggested 2015-02-13 by Philippe Spindel
See also:: Annotations for §5.10 and Ch.5

…

7: 14.31 Other Applications

… ►The conical functions

\mathsf{P}^{m}_{-\frac{1}{2}+i\tau}\left(x\right)

appear in boundary-value problems for the Laplace equation in toroidal coordinates (§14.19(i)) for regions bounded by cones, by two intersecting spheres, or by one or two confocal hyperboloids of revolution (Kölbig (1981)). …

8: 33.23 Methods of Computation

… ►Bardin et al. (1972) describes ten different methods for the calculation of

F_{\ell}

and

G_{\ell}

, valid in different regions of the (

\eta,\rho

)-plane. … ►Hull and Breit (1959) and Barnett (1981b) give WKBJ approximations for

F_{0}

and

G_{0}

in the region inside the turning point:

\rho<\rho_{\operatorname{tp}}\left(\eta,\ell\right)

9: 19.7 Connection Formulas

… ►The first of the three relations maps each circular region onto itself and each hyperbolic region onto the other; in particular, it gives the Cauchy principal value of

\Pi\left(\phi,\alpha^{2},k\right)

when

\alpha^{2}>{\csc}^{2}\phi

(see (19.6.5) for the complete case). … ►The second relation maps each hyperbolic region onto itself and each circular region onto the other: … ►The third relation (missing from the literature of Legendre’s integrals) maps each circular region onto the other and each hyperbolic region onto the other: …

10: 19.21 Connection Formulas

… ►Change-of-parameter relations can be used to shift the parameter

p

R_{J}

from either circular region to the other, or from either hyperbolic region to the other (§19.20(iii)). … ►For each value of

p

, permutation of

x, y, z

produces three values of

q

, one of which lies in the same region as

p

and two lie in the other region of the same type. In (19.21.12), if

x

is the largest (smallest) of

x, y

, and

z

, then

p

and

q

lie in the same region if it is circular (hyperbolic); otherwise

p

and

q

lie in different regions, both circular or both hyperbolic. …